【数据结构与算法Python版学习笔记】树——平衡二叉搜索树（AVL树）

定义

• 能够在key插入时一直保持平衡的二叉查找树： AVL树
• 利用AVL树实现ADT Map， 基本上与BST的实现相同，不同之处仅在于二叉树的生成与维护过程

平衡因子

• AVL树的实现中， 需要对每个节点跟踪“平衡因子balance factor”参数

  $balance Factor=height (left SubTree)-height(right SubTree)$

  • 平衡因子大于0，称为“左重left-heavy”，
  • 小于零称为“右重right-heavy”
  • 平衡因子等于0，则称作平衡。

• 如果一个二叉查找树中每个节点的平衡因子都在-1， 0， 1之间， 则把这个二叉搜索树称为平衡树

  • 在平衡树操作过程中， 有节点的平衡因子超出此范围， 则需要一个重新平衡的过程

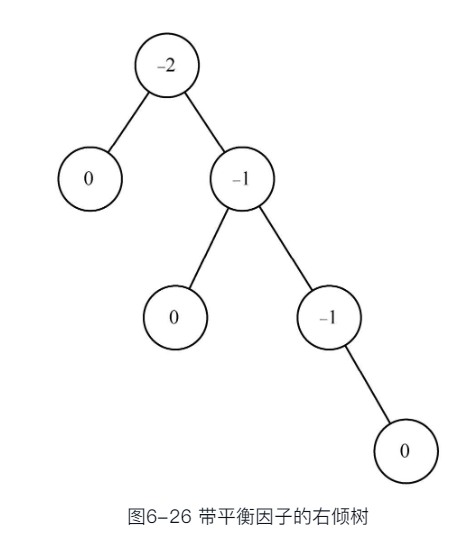
AVL树的性能

问题规模（总节点数N）和比对次数（树的高度h）之间的关系

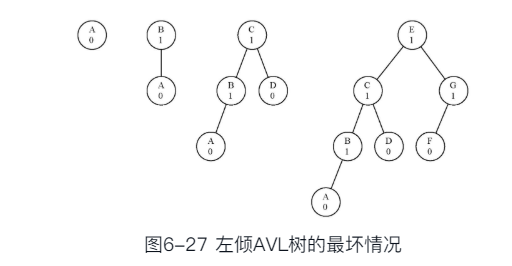
最差情形下的性能：即平衡因子为1或者-1

• 当高度为h时，节点数Nh是：Nh=1+Nh-1+Nh-2
  • 与斐波那契数列很相似，随着斐波那契数列的增长，Fi/Fi-1逐渐逼近黄金分割比例Φ
  • 最多搜索次数h和规模N的关系， 可以说AVL树的搜索时间复杂度为O(log n)

实现

• 首先， 作为BST， 新key必定以叶节点形式插入到AVL树中
  • 叶节点的平衡因子是0， 其本身无需重新平衡
  • 但会影响其父节点的平衡因子：
    • 作为左子节点插入，则父节点平衡因子会增加1；
    • 作为右子节点插入，则父节点平衡因子会减少1。
  • 这种影响可能随着其父节点到根节点的路径一直传递上去， 直到：
    • 传递到根节点为止；
    • 或者某个父节点平衡因子被调整到0，不再影响上层节点的平衡因子为止

重新定义_put方法即可

def _put(self, key, val, currentNode):
    if key < currentNode.key:
        if currentNode.hasLeftChild():
            self._put(key, val, currentNode.leftChild)
        else:
            currentNode.leftChild = TreeNode(key, val, parent=currentNode)
            # 调整因子
            self.updateBalance(currentNode.leftChild)
    else:
        if currentNode.hasRightChild():
            self._put(key, val, currentNode.rightChild)
        else:
            currentNode.rightChild = TreeNode(key, val, parent=currentNode)
            # 调整因子
            self.updateBalance(currentNode.rightChild)

def updateBalance(self, node):
    if node.balanceFactor > 1 or node.balanceFactor < -1:
        self.rebalance(node)
    if node.parent != None:
        if node.isLeftChild():
            node.parent.balanceFactor += 1
        if node.isRightChild():
            node.parent.balanceFactor-+1

        if node.parent.balanceFactor != 0:
            updateBalance(node.parent)

rebalance重新平衡

• 主要手段 ：将不平衡的子树进行旋转rotation
• 视“左重”或者“右重”进行不同方向的旋转

左旋包括以下步骤:

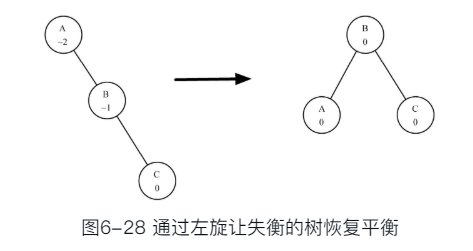
• 将右子节点（节点B）提升为子树的根节点。
• 将旧根节点（节点A）作为新根节点的左子节点。
• 如果新根节点（节点B）已经有一个左子节点，将其作为新左子节点（节点A）的右子节点。注意，因为节点B之前是节点A的右子节点，所以此时节点A必然没有右子节点。因此，可以为它添加新的右子节点，而无须过多考虑。

def rotateLeft(self, rotRoot):
    newRoot = rotRoot.rightChild
    rotRoot.rightChild = newRoot.leftChild
    if newRoot.leftChild != None:
        newRoot.leftChild.parent = rotRoot
    newRoot.parent = rotRoot.parent
    if rotRoot.isRoot():
        self.root = newRoot
    else:
        if rotRoot.isLeftChild():
            rotRoot.parent.leftChild = newRoot
        else:
            rotRoot.parent.rightChild = newRoot
    newRoot.leftChild = rotRoot
    rotRoot.parent = newRoot
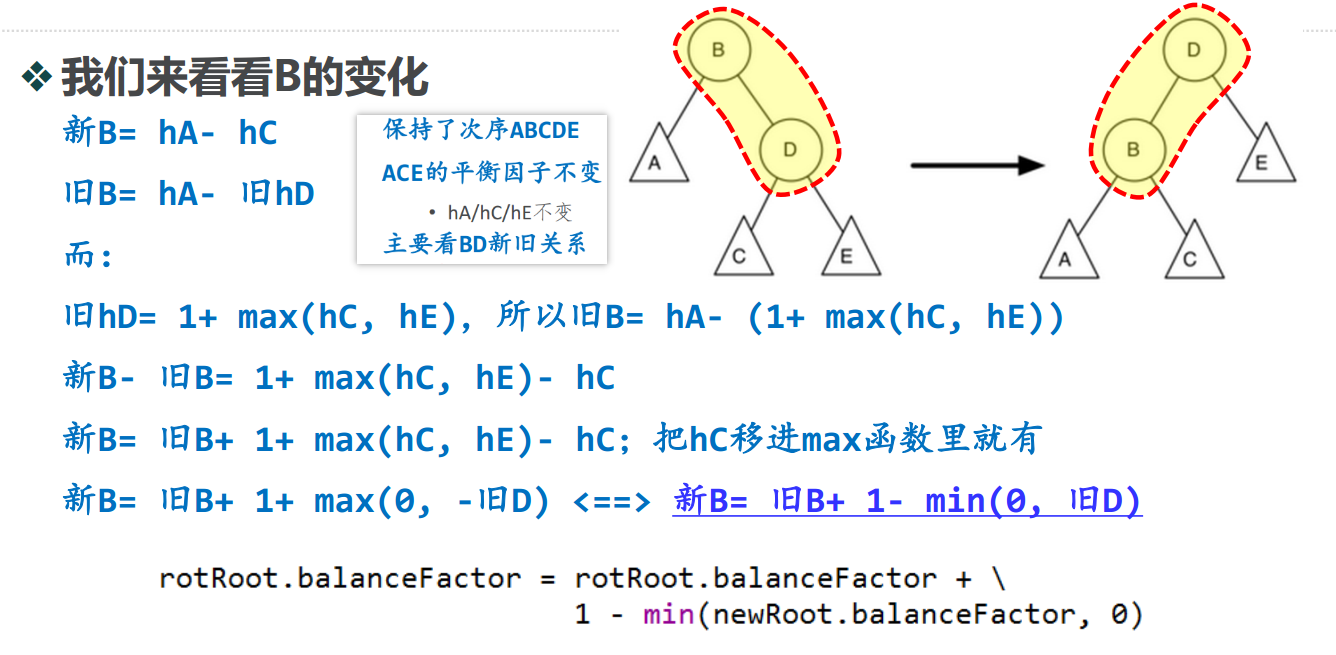
    rotRoot.balanceFactor = rotRoot.balanceFactor + \
        1-min(newRoot.balanceFactor, 0)
    newRoot.balanceFactor = newRoot.balanceFactor + \
        1+max(rotRoot.balanceFactor, 0)

右旋步骤如下。

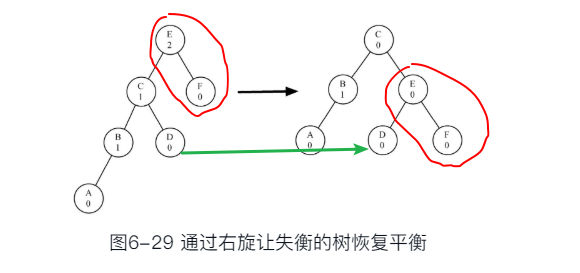
• 将左子节点（节点C）提升为子树的根节点。
• 将旧根节点（节点E）作为新根节点的右子节点。
• 如果新根节点（节点C）已经有一个右子节点（节点D），将其作为新右子节点（节点E）的左子节点。注意，因为节点C之前是节点E的左子节点，所以此时节点E必然没有左子节点。因此，可以为它添加新的左子节点，而无须过多考虑。

如何调整平衡因子

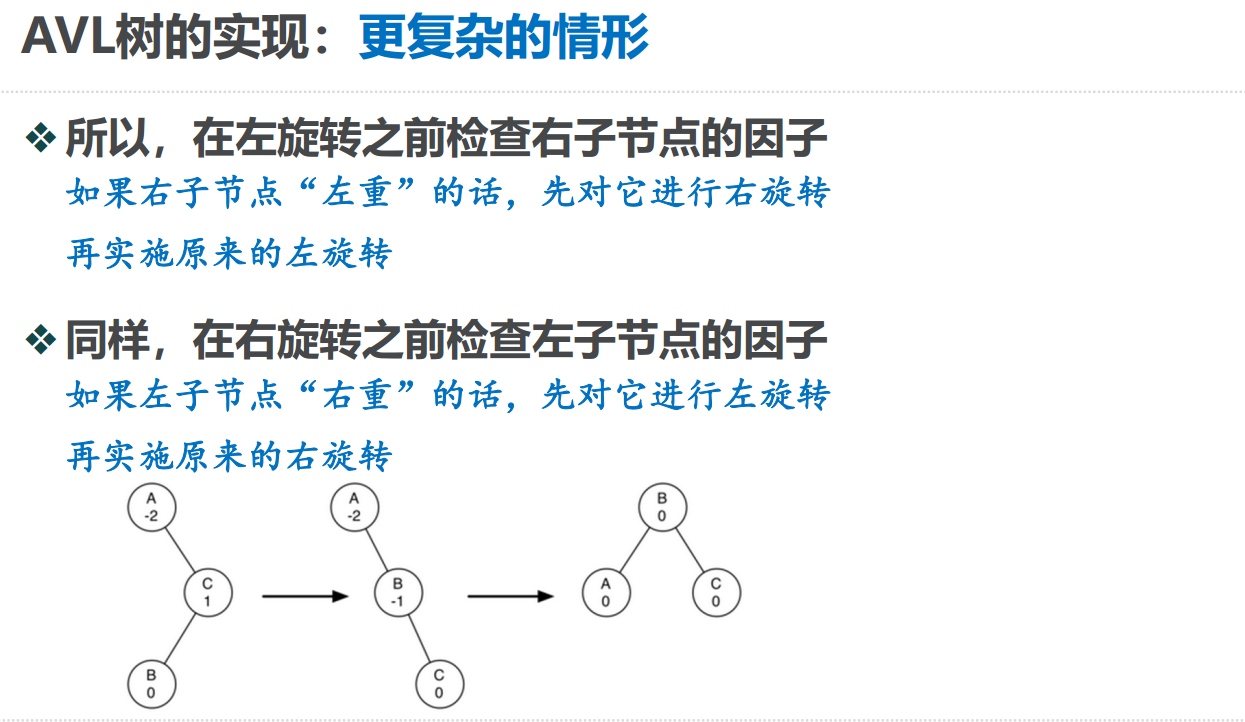
def rebalance(self,node):
    # 右重左旋
    if node.balanceFactor<0:
        # 右子节点左重右旋
        if node.rightChild.balanceFactor>0:
            self.rotateRight(node.rightChild)
            self.rotateLeft(node)
        else:
            self.rotateLeft(node)
    # 左重右旋
    elif node.balanceFactor>0:
        # 左子节点右重左旋
        if node.leftChild.balanceFactor<0:
            self.rotateLeft(node.leftChild)
            self.rotateRight(node)
        else:
            self.rotateRight(node)

结语

• 经过复杂的put方法， AVL树始终维持平衡， get方法也始终保持O(log n)高性能
• 整个put方法的时间复杂度还是O(log n)
  • 需要插入的新节点是叶节点，更新其所有父节点和祖先节点的代价最多为O(log n)
  • 如果插入的新节点引发了不平衡，重新平衡最多需要2次旋转，但旋转的代价与问题规模无关，是常数O(1)