【数据结构与算法Python版学习笔记】树——二叉查找树 Binary Search Tree

• 二叉搜索树，它是映射的另一种实现
• 映射抽象数据类型前面两种实现，它们分别是列表二分搜索和散列表。

操作

• Map()新建一个空的映射。

• put(key, val)往映射中加入一个新的键-值对。如果键已经存在，就用新值替换旧值。

• get(key)返回key对应的值。如果key不存在，则返回None。

• del通过del map[key]这样的语句从映射中删除键-值对。

• len()返回映射中存储的键-值对的数目。

• in通过key in map这样的语句，在键存在时返回True，否则返回False。

二叉查找树BST的性质

• 比父节点小的key都出现在左子树，比父节点大的key都出现在右子树。
• 注意：插入顺序不同， 生成的BST也不同

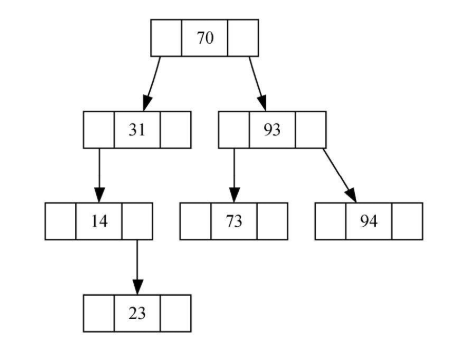
二叉搜索树的实现：节点和链接结构

思路

• 需要用到BST和TreeNode两个类， BST的root成员引用根节点TreeNode

put(key, val)方法：插入key构造BST

• 首先看BST是否为空，如果一个节点都没有，那么key成为根节点root
• 否则，就调用一个递归函数_put(key, val,root)来放置key
• _put辅助方法
  • 如果key比currentNode小，那么_put到左子树
    • •但如果没有左子树，那么key就成为左子节点
  • 如果key比currentNode大，那么_put到右子树
    • 但如果没有右子树，那么key就成为右子节点

BST.remove方法

• 这个节点没有子节点
  直接删除
• 这个节点有1个子节点
  解决：将这个唯一的子节点上移，替换掉被删节点的位置
  • 被删节点的子节点是左？还是右子节点？
  • 被删节点本身是其父节点的左？还是右子节点？
  • 被删节点本身就是根节点？
• 这个节点有2个子节点
  • 无法简单地将某个子节点上移替换被删节点，但可以找到另一个合适的节点来替换被删节点，这个合适节点就是被删节点的下一个key值节点，即被删节点右子树中最小的那个，称为“后继”
  • 可以肯定这个后继节点最多只有1个子节点（本身是叶节点，或仅有右子树）
  • 将这个后继节点摘出来（也就是删除了），替换掉被删节点

代码

binarySearchTree类

# 二叉搜索树的实现：节点和链接结构
class binarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size
		
		# 直接调用了TreeNode中的同名方法
    def __iter__(self):
        return self.root.__iter__()

    # 首先看BST是否为空，如果一个节点都没有，那么key成为根节点root
    # 否则，就调用一个递归函数_put(key, val,root)来放置key
    def put(self, key, val):
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = TreeNode(key, val)
        self.size += 1

    # 如果key比currentNode小，那么_put到左子树
    # • 但如果没有左子树，那么key就成为左子节点
    # 如果key比currentNode大，那么_put到右子树
    # • 但如果没有右子树，那么key就成为右子节点
    def _put(self, key, val, currentNode):
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                self._put(key, val, currentNode.leftChild)
            else:
                currentNode.leftChild = TreeNode(key, val, parent=currentNode)
        else:
            if currentNode.hasRightChild():
                self._put(key, val, currentNode.rightChild)
            else:
                currentNode.rightChild = TreeNode(key, val, parent = currentNode)

    def __setitem__(self, k, v):
        self.put(k, v)

    def get(self,key):
        if self.root:
            res=self._get(key,self.root)
            if res !=None:
                #print("      ",res.key,res.payload)
                return res.payload
            else:
                return None
        else:
            return None
    
    def _get(self,key,currentNode):
        if not currentNode:
            return None
        elif currentNode.key==key:
            return currentNode
        elif key<currentNode.key:
            return self._get(key,currentNode.leftChild)
        else:
            return self._get(key,currentNode.rightChild)

		#实现val= myZipTree['PKU']
    def __getitem__(self, key):
        return self.get(key)

		# 实现'PKU' in myZipTree的归属判断运算符in
    def __contains__(self,key):
        if self._get(key,self.root):
            return True
        else:
            return False

    def delete(self,key):
        if self.size>1:
            nodeToRemove=self._get(key,self.root)
            if nodeToRemove:
                self.remove(nodeToRemove)
                self.size-=1
            else:
                raise KeyError('Error, key not in tree')
        elif self.size==1 and self.root.key==key:
            self.root=None
            self.size-=1
        else:
            raise KeyError('Error, key not in tree')

    def remove(self,currentNode):
        # 当前节点是叶节点
        
        if currentNode.isLeaf():
            if currentNode==currentNode.parent.leftChild:
                currentNode.parent.leftChild=None
            else:
                currentNode.parent.rightChild=None
        # 当前节点有两个节点
        elif currentNode.hasBothChildren():
            succ=currentNode.findSuccessor()
            succ.spliceOut()
            currentNode.key=succ.key
            currentNode.payload=succ.payload
        # 当前节点只有一个节点
        else:
            if currentNode.hasLeftChild(): # 当前节点具有左子树
                if currentNode.isLeftChild(): # 当前节点作为左子节点删除
                    currentNode.leftChild.parent=currentNode.parent
                    currentNode.parent.leftChild=currentNode.leftChild
                elif currentNode.isRightChild(): # 当前节点作为右子节点删除
                    currentNode.leftChild.parent=currentNode.parent
                    currentNode.parent.leftChild=currentNode.leftChild
                else: # 当前节点作为根节点删除
                    currentNode.replaceNodeData(currentNode.leftChild.key,
                    currentNode.leftChild.payload,
                    currentNode.leftChild.leftChild,
                    currentNode.leftChild.rightChild
                    )
            else: # 当前节点具有右子树
                if currentNode.isLeftChild(): # 当前节点作为左子节点删除
                    currentNode.rightChild.parent=currentNode.parent
                    currentNode.parent.leftChild=currentNode.rightChild
                elif currentNode.isRightChild():# 当前节点作为右子节点删除
                    currentNode.rightChild.parent=currentNode.parent
                    currentNode.parent.rightChild=currentNode.rightChild
                else:# 当前节点作为根节点删除
                    currentNode.replaceNodeData(currentNode.rightChild.key,
                    currentNode.rightChild.payload,
                    currentNode.rightChild.leftChild,
                    currentNode.rightChild.rightChild
                    )

 
		# 实现del myZipTree['PKU']这样的语句操作
    def __delitem__(self,key):
        self.delete(key)

TreeNode类

class TreeNode:
    def __init__(self, key, val, left=None, right=None, parent=None):
        self.key = key  # 键值
        self.payload = val  # 数据项
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return self.rightChild

    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    def isRoot(self):
        return not self.parent

    def isLeaf(self):
        return not (self.rightChild or self.leftChild)

    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    def hasBothChildren(self):
        return self.rightChild and self.leftChild

    def replaceNodeData(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild:
            self.leftChild.parent = self
        if self.hasRightChild:
            self.rightChild.parent = self

    def __iter__(self):
        '''中序遍历迭代'''
        if self:
            if self.hasLeftChild():
                for elem in self.leftChild: # 迭代
                    yield elem # 对每次迭代返回的值，类似于生成器
            yield self.key
            if self.hasRightChild():
                for elem in self.rightChild:
                    yield elem

   # 寻找后继节点
    def findSuccessor(self):
        succ=None
        if self.hasRightChild():
            succ=self.rightChild.finMin()
        else:# 目前不会遇到
            if self.parent:
                if self.isLeftChild():
                    succ=self.parent
                else:
                    self.parent.rightChild=None
                    succ=self.parent.findSuccessor()
                    self.parent.rightChild=self
        return succ

    def finMin(self):
        current=self
        while current.hasLeftChild():
            current=current.leftChild
        return current    

    # 摘出节点
    def spliceOut(self):
        if self.isLeaf():
            if self.isLeftChild():
                self.parent.leftChild=None
            else:
                self.parent.rightChild=None
        elif self.hasAnyChildren():
            if self.hasLeftChild():
                if self.isLeftChild():
                    self.parent.leftChild=self.leftChild
                else:
                    self.parent.rightChild=self.leftChild
                self.leftChild.parent=self.parent
            else:
                if self.isLeftChild():
                    self.parent.leftChild=self.rightChild
                else:
                    self.parent.rightChild=self.rightChild
                self.rightChild.parent=self.parent

• 调用

if __name__ == "__main__":
    mytree=binarySearchTree()
    mytree[3]='red'
    mytree[4]='blue'
    mytree[6]='yellow'
    mytree[2]='at'

    print(3 in mytree)
    print(mytree[6])

    del mytree[3]
    print(mytree[2])
    for key in mytree:
        print(key,mytree[key])

---

算法分析

• 其性能决定因素在于二叉搜索树的高度（最大层次） ， 而其高度又受数据项key插入顺序的影响。
• 如果key的列表是随机分布的话， 那么大于和小于根节点key的键值大致相等
• BST的高度就是log2n（n是节点的个数） ，而且， 这样的树就是平衡树
• put方法最差性能为O(logn)。
• 但key列表分布极端情况就完全不同
  按照从小到大顺序插入的话，如下图。这时候put方法的性能为O(n)。其它方法也是类似情况

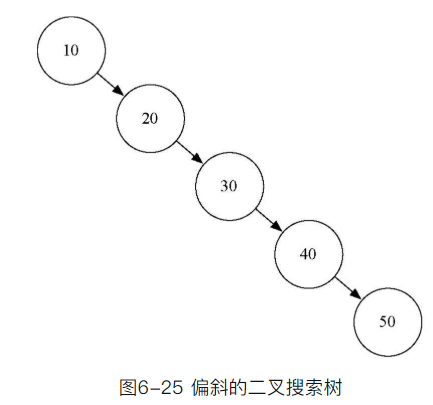
• 对于不平衡的树来说，最坏情况下的时间复杂度仍是O(n)