【数据结构与算法Python版学习笔记】查找与排序——散列、散列函数、区块链

散列 Hasing

前言

如果数据项之间是按照大小排好序的话，就可以利用二分查找来降低算法复杂度。
- 现在我们进一步来构造一个新的数据结构，能使得查找算法的复杂度降到O(1)，这种概念称为“散列Hashing“
能够使得查找的次数降低到常数级别，我们对数据项所处的位置就必须有更多的先验知识。
- 如果我们事先能知道要找的数据项应该出现在数据集中的什么位置，就可以直接到那个位置看看数据项是否存在即可
- 由数据项的值来确定其存放位置

基本概念

散列表（hash table，又称哈希表）是一种数据集，其中数据项的存储方式尤其有利于将来快速的查找定位。
散列表中的每一个存储位置，称为槽（slot），可以用来保存数据项，每个槽有一个唯一的名称。
实现从数据项到存储槽名称的转换的，称为散列函数（hash function）

槽被数据项占据的比例称为散列表的“负载因子”，这里负载因子为6/11
要查找某个数据项是否存在于表中，我们只需要使用同一个散列函数，对查找项进行计算，测试下返回的槽号所对应的槽中是否有数据项即可
实现了O(1)时间复杂度的查找算法
分配到同一个槽中，这种情况称为“冲突collision”

完美散列函数

定义

给定一组数据项，如果一个散列函数能把每个数据项映射到不同的槽中，那么这个散列函数就可以称为“完美散列函数”
但如果数据项经常性的变动，很难有一个系统性的方法来设计对应的完美散列函数

获得方法

扩大散列表的容量，大到所有可能出现的数据项都能够占据不同的槽
- 但这种方法对于可能数据项范围过大的情况并不实用
  假如我们要保存手机号（11位数字），完美散列函数得要求散列表具有百亿个槽！会浪费太多存储空间
好的散列函数需要具备特性
- 冲突最少（近似完美）
- 计算难度低（额外开销小）
- 充分分散数据项（节约空间）

散列函数MD5/SHA

MD5（Message Digest）将任何长度的数据变换为固定长为128位（16字节）的“摘要”
SHA（Secure Hash Algorithm）是另一组散列函数
- SHA-0/SHA-1输出散列值160位（20字节），
- SHA-256/SHA-224分别输出256位、 224位，
- SHA-512/SHA-384分别输出512位和384位
Python自带MD5和SHA系列的散列函数库： hashlib

import hashlib
print(hashlib.md5("hello world".encode("utf-8")).hexdigest())
print(hashlib.sha1("hello world".encode("utf-8")).hexdigest())

>>>
5eb63bbbe01eeed093cb22bb8f5acdc3
2aae6c35c94fcfb415dbe95f408b9ce91ee846ed

import hashlib
m=hashlib.md5()
m.update("hello world".encode("utf-8"))
m.update("this is part #2".encode("utf-8"))
m.update("this is part #3".encode("utf-8"))
print(m.hexdigest())

应用：完美散列函数用于数据一致性校验

数据文件一致性判断
为每个文件计算其散列值，仅对比其散列值即可得知是否文件内容相同；
用于网络文件下载完整性校验；
用于文件分享系统：网盘中相同的文件（尤其是电影）可以无需存储多次
加密形式保存密码
仅保存密码的散列值，用户输入密码后，计算散列值并比对；
无需保存密码的明文即可判断用户是否输入了正确的密码。
防文件篡改：原理同数据文件一致性判断
彩票投注应用
彩民下注前，机构将中奖的结果散列值公布，然后彩民投注，开奖后，彩民可以通过公布的结果和散列值对比，验证机构是否作弊。

区块链技术

概念

区块链是一种分布式数据库通过网络连接的节点每个节点都保存着整个数据库所有数据任何地点存入的数据都会完成同步
区块链最本质特征是“去中心化”不存在任何控制中心、协调中心节点所有节点都是平等的，无法被控制

数据结构

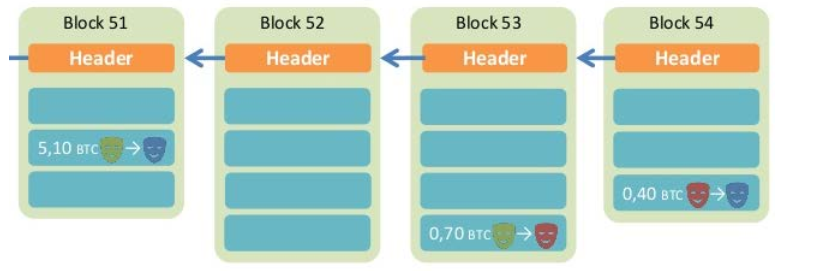
区块链由一个个区块（block）组成，区块分为头（head）和体（body）
- 区块头记录了区块的信息
  生成时间、前一个区块(head+body)的散列值
- 区块体记录了实际数据

不可修改性

由于散列值具有抗修改性，任何对某个区块数据的改动必然引起散列值的变化
为了不导致这个区块脱离链条，就需要修改所有后续的区块
由于有“工作量证明”的机制，这种大规模修改不可能实现的，除非掌握了全网51%以的计算力

工作量证明： Proof of Work(POW)

由于区块链是大规模的分布式数据库，同步较慢，新区块的添加速度需要得到控制
目前最大规模区块链Bitcoin采用的速度是平均每10分钟生成一个区块
大家不惜付出海量的计算，去抢着算出一个区块的有效散列值
最先算出的那位“矿工”才有资格把区块挂到区块链中

为什么有效散列值那么难算出？

矿工的工作是，找到一个数值Nonce，把它跟整个区块数据一起计算散列，这个散列值必须小于target，才是有效的散列值
由于散列值无法回推原值，这个Nonce的寻找只能靠暴力穷举，计算工作量+运气是唯一的方法。

为什么矿工抢着生成区块？

因为有利益！
在加密货币Bitcoin中，区块内包含的数据是“交易记录”，也就是“账本”，这对于货币体系至关重要
Bitcoin规定，每个区块中包含了一定数量的比特币作为“记账奖励”，这样就鼓励了更多人加入到抢先记账的行列
由于硬件摩尔定律的存在，计算力将持续递增，为了维持每10分钟生成一个区块的速度，难度系数Difficulty也将持续递增
另外，为了保持货币总量不会无限增加，每4年奖励的比特币减半
2008年开始是50个， 2019年为12.5个

散列函数设计

折叠法

将数据项按照位数分为若干段，
再将几段数字相加，
最后对散列表大小求余，得到散列值

例如， 对电话号码62767255可以两位两位分为4段（62、 76、 72、 55）
相加（62+76+72+55=265）
散列表包括11个槽，那么就是265%11=1
所以h(62767255)=1

有时候折叠法还会包括一个隔数反转的步骤(一种微调手段)

比如（62、 76、 72、 55）隔数反转为（62、 67、 72、 55）
再累加（62+67+72+55=256）
对11求余（256%11=3），所以h'(62767255)=3

平方取中法

平方取中法，首先将数据项做平方运算，
然后取平方数的中间两位，再对散列表的
大小求余

例如， 对44进行散列
首先44*44=1936
然后取中间的93
对散列表大小11求余， 93%11=5

折叠法与平方取中法比较

两个都是完美散列函数
分散度都很好
平方取中法计算量稍大

非数项

我们也可以对非数字的数据项进行散列，把字符串中的每个字符看作ASCII码即可
再将这些整数累加，对散列表大小求余

如cat， ord('c')==99, ord('a')==96,ord('t')==116

def hash(astring, tablesize):
    sum = 0
    for pos in range(len(astring)):
        sum = sum + ord(astring[pos])
    return sum % tablesize

u3 = hash('hello', 11)
print(u3)

缺陷与解决方法

这样的散列函数对所有的变位词都返回相同的散列值
为了防止这一点，可以将字符串所在的位置作为权重因子，乘以ord值

散列函数设计原则

散列函数不能成为存储过程和查找过程的计算负担
如果散列函数设计太过复杂，去花费大量的计算资源计算槽号。可能还不如简单地进行顺序查找或者二分查找
失去了散列本身的意义

冲突解决方案

概念

如果两个数据项被散列映射到同一个槽，需要一个系统化的方法在散列表中保存第二个数据项，这个过程称为“解决冲突”
如果说散列函数是完美的，那就不会有散列冲突，但完美散列函数常常是不现实的

方法1：开放定址 open addressing —— 寻找空槽的技术

解决散列的一种方法就是为冲突的数据项再找一个开放的空槽来保存
最简单的就是从冲突的槽开始往后扫描，直到碰到一个空槽
如果到散列表尾部还未找到，则从首部接着扫描

线性探测linear probing —— 向后逐个槽寻找的方法

采用线性探测方法来解决散列冲突的话，则散列表的查找也遵循同样的规则
- 如果在散列位置没有找到查找项的话，就必须向
- 后做顺序查找直到找到查找项，或者碰到空槽（查找失败）。
缺点：有聚集（clustering）的趋势
连锁式影响其它数据项的插入
改进：避免聚集的一种方法就是将线性探测扩展，从逐个探测改为跳跃式探测

再散列rehashing

重新寻找空槽的过程可以用一个更为通用的“再散列rehashing”来概括
跳跃式探测中，
- 需要注意的是skip的取值，不能被散列表大小整除，否则会产生周期，造成很多空槽永远无法探测到
- 一个技巧是，把散列表的大小设为素数，如例子的11
还可以将线性探测变为 “二次探测quadratic probing”
- 不再固定skip的值，而是逐步增加skip值，如1、 3、 5、 7、 9
- 这样槽号就会是原散列值以平方数增加：h, h+1, h+4, h+9, h+16...

方法2：数据项链Chaining

概念

将容纳单个数据项的槽扩展为容纳数据项集合（或者对数据项链表的引用）
散列表中的每个槽就可以容纳多个数据项，如果有散列冲突发生，只需要简单地将数据项添加到数据项集合中。
查找数据项时则需要查找同一个槽中的整个集合，当然，随着散列冲突的增加，对数据项的查找时间也会相应增加。

映射抽象数据类型 ADT Map

字典

字典是一种可以保存key-data键值对的数据类型
这种键值关联的方法称为“映射Map“
ADT Map的结构是键-值关联的无序集合
- 关键码具有唯一性
- 通过关键码可以唯一确定一个数据值

实现ADT Map：应用实例

下面，我们用一个HashTable类来实现ADT Map，该类包含了两个列表作为成员
- 其中一个slot列表用于保存key
- 另一个平行的data列表用于保存数据项
在slot列表查找到一个key的位置以后，在data列表对应相同位置的数据项即为关联数据

class HashTable:
    def __init__(self):
        self.size=11
        self.slots=[None]*self.size
        self.data=[None]*self.size

    def __getitem__(self,key):
        return self.get(key)

    def __setitem__(self,key,data):
        self.put(key,data)

    def hashfunction(self,key):
        return key% self.size

    def rehash(self,oldhash):
        return (oldhash+1)%self.size

    def put(self,key,data):
        hashvalue=self.hashfunction(key)

        if self.slots[hashvalue]==None: # 新槽，不冲突
            self.slots[hashvalue]=key
            self.data[hashvalue]=data
        else:
            if self.slots[hashvalue]==key: # 找到槽，更新数据
                self.data[hashvalue]=data
            else: # 寻找新槽
                nextslot=self.rehash(hashvalue)
                while self.slots[nextslot]!=None and self.slots[nextslot] !=key:
                    nextslot=self.rehash(hashvalue)

                if self.slots[nextslot]==None:# 新槽，不冲突
                    self.slots[nextslot]=key
                    self.data[nextslot]=data
                else:
                    self.data[nextslot]=data #更新数据
    
    def get(self,key):
        # 标记散列值为查找起点
        startslot=self.hashfunction(key)

        data=None
        stop=False
        found=False
        position=startslot
        # 找key，直到空槽或回到起点
        while self.slots[position]!=None and not found and not stop:
            if self.slots[position]==key:
                found=True
                data=self.data[position]
            # 未找到key，再散列继续找
            else:
                position=self.rehash(position)
                if position==startslot:
                    stop=True
        return data

if __name__ == "__main__":
    H = HashTable()
    H[54] = "cat"
    H[26] = "dog"
    H[20] = "chicken"
    print(H.slots)
    print(H.data)
    print(H[20])

>>>
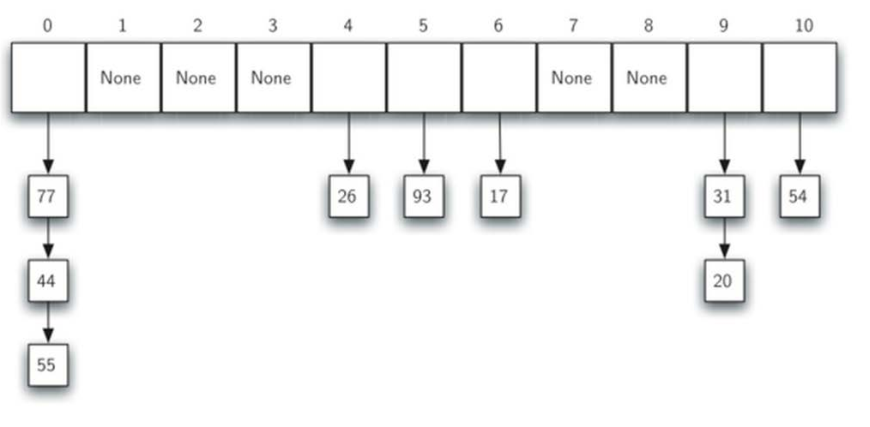
[None, None, None, None, 26, None, None, None, None, 20, 54]
[None, None, None, None, 'dog', None, None, None, None, 'chicken', 'cat']
chicken

散列算法分析

散列在最好的情况下，可以提供O(1)常数级时间复杂度的查找性能
由于散列冲突的存在，查找比较次数就没有这么简单
评估散列冲突的最重要信息就是负载因子λ，一般来说：
- 如果λ较小，散列冲突的几率就小，数据项通常会保存在其所属的散列槽中
- 如果λ较大，意味着散列表填充较满，冲突会越来越多，冲突解决也越复杂，也就需要更多的比较来找到空槽；如果采用数据链的话，意味着每条链上的数据项增多
如果采用线性探测的开放定址法来解决冲突（λ在0~1之间）
如果采用数据链来解决冲突（λ可大于1）

posted @ 2021-04-22 14:07 砥才人阅读(353) 评论(0) 编辑收藏举报

刷新页面返回顶部

代码质疑人生

万里步尘砥才人

代码质疑人生

【数据结构与算法Python版学习笔记】查找与排序——散列、散列函数、区块链

散列 Hasing

前言

基本概念

完美散列函数

定义

获得方法

更多用途

散列函数MD5/SHA

应用：完美散列函数用于数据一致性校验

区块链技术

概念

数据结构

不可修改性

工作量证明： Proof of Work(POW)

为什么有效散列值那么难算出？

为什么矿工抢着生成区块？

散列函数设计

折叠法

平方取中法

折叠法与平方取中法比较

非数项

缺陷与解决方法

散列函数设计原则

冲突解决方案

概念

方法1：开放定址 open addressing —— 寻找空槽的技术

线性探测linear probing —— 向后逐个槽寻找的方法

再散列rehashing

方法2：数据项链Chaining

概念

映射抽象数据类型 ADT Map

字典

实现ADT Map：应用实例

散列算法分析

公告