【数据结构与算法Python版学习笔记】查找与排序——排序：冒泡、选择、插入、希尔、归并、快速

---

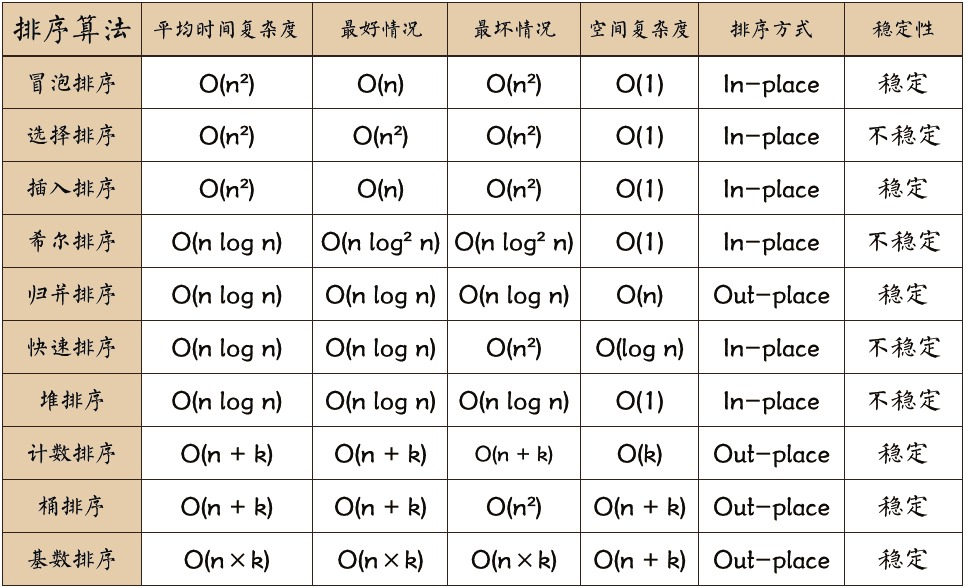
冒泡排序O(n²) —— bubbleSort

定义

冒泡排序多次遍历列表。它比较相邻的元素，将不合顺序的交换。每一轮遍历都将下一个最大值放到正确的位置上。本质上，每个元素通过“冒泡”找到自己所属的位置。

• 冒泡排序的算法思路在于对无序表进行多趟比较交换，
• 每趟包括了多次两两相邻比较， 并将逆序的数据项互换位置， 最终能将本趟的最大项就位
• 经过n-1趟比较交换， 实现整表排序
• 每趟的过程类似于“气泡”在水中不断上浮到水面的经过

算法分析

• 比对次数： $\frac{1}{2}n^2-\frac{1}{2}n$

• 时间复杂度O(n²)

• 最好的情况是列表在排序前已经有序， 交换次数为0

• 最差的情况是每次比对换次数等于比对次数

• 平均情况则是最差情况的一半

• 优势
  无需任何额外的存储空间开销

• 性能改进
  通过监测每趟比对是否发生过交换，可以提前确定排序是否完成

代码

• 基本实现

def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1]=alist[i+1],alist[i]

if __name__ == "__main__":
    alist=[54,26,93,17,77,31,44,55]
    bubbleSort(alist)
    print(alist)

• 改进

def bubbleSort2(alist):
    exchanges=True
    passnum=len(alist)-1
    while passnum>0 and exchanges:
        exchanges=False
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                exchanges=True
                alist[i],alist[i+1]=alist[i+1],alist[i]
        passnum-=1

if __name__ == "__main__":
    alist=[54,26,93,17,77,31,44,55]
    bubbleSort2(alist)
    print(alist)

---

选择排序O(n²) —— selectionSort

定义

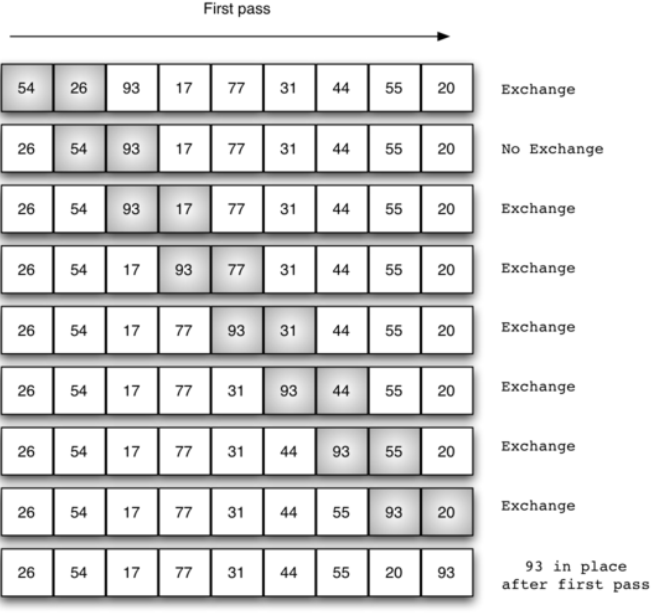
• 选择排序对冒泡排序进行了改进， 保留了其基本的多趟比对思路， 每趟都使当前最大项就位。
• 但选择排序对交换进行了削减， 相比起冒泡排序进行多次交换， 每趟仅进行1次交换， 记录最大项的所在位置， 最后再跟本趟最后一项交换
• 选择排序的时间复杂度比冒泡排序稍优

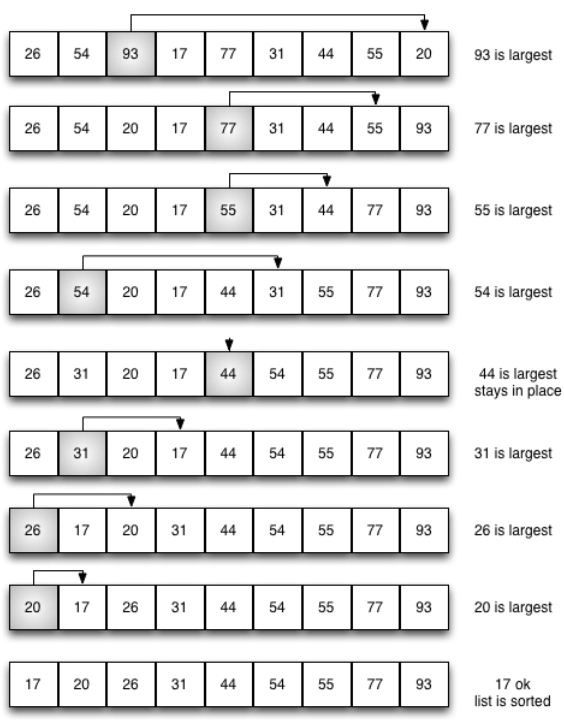
算法分析

• 比对次数不变，还是O(n²)
• 交换次数则减少为O(n)

代码

def selectionSort(alist):
    for fillslot in range(len(alist)-1,0,-1):
        positionOfMax=0
        for location in range(1,fillslot+1):
            if alist[positionOfMax]<alist[location]:
                positionOfMax=location
        alist[fillslot],alist[positionOfMax]=alist[positionOfMax],alist[fillslot]

if __name__ == "__main__":
    alist=[54,26,93,17,77,31,44,55]
    selectionSort(alist)
    print(alist)

---

插入排序O(n²) —— Insertion Sort

定义

• 插入排序维持一个已排好序的子列表， 其位置始终在列表的前部， 然后逐步扩大这个子列表直到全表

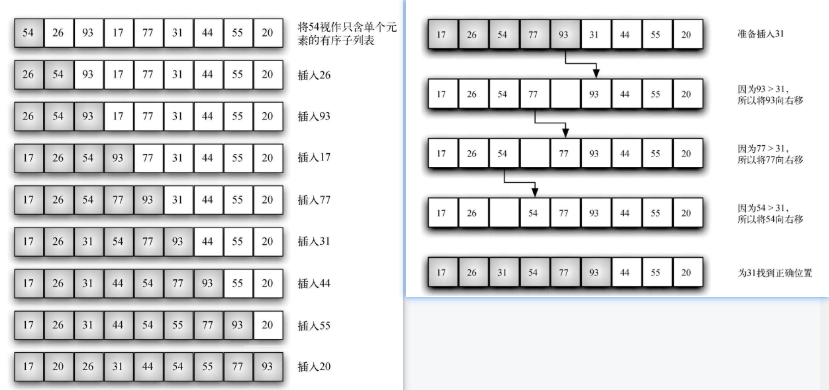
代码

def insertionSort(alist):
    for index in range(1, len(alist)):
        position = index
        currentvalue = alist[index]

        while position > 0 and alist[position-1] > currentvalue:
            alist[position] = alist[position-1]
            position -= 1
        alist[position] = currentvalue

if __name__ == "__main__":
    alist = [54, 26, 93, 17, 77, 31, 44, 55]
    insertionSort(alist)
    print(alist)

希尔排序 —— Shell Sort

定义

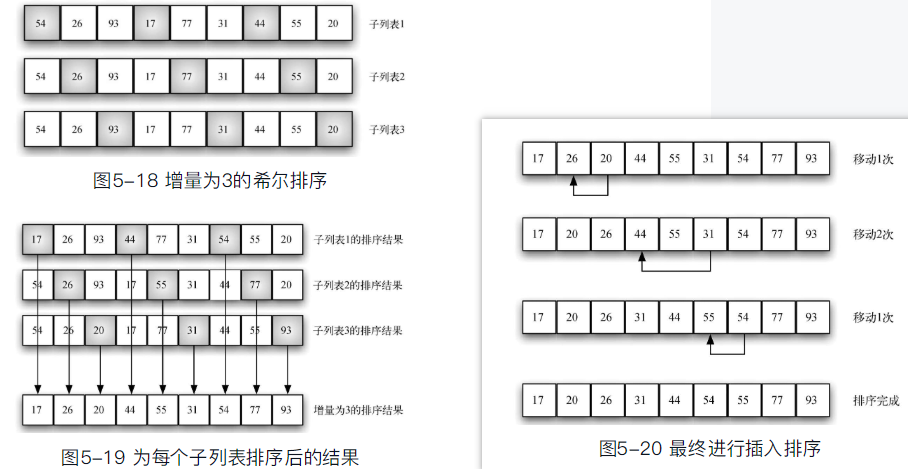
• 希尔排序也称“递减增量排序”，它对插入排序做了改进，将列表分成数个子列表，并对每一个子列表应用插入排序
• 列表越接近有序， 插入排序的比对次数就越少
• 希尔排序以插入排序作为基础， 对无序表进行“间隔”划分子列表， 每个子列表都执行插入排序
• 子列表的间隔一般从n/2开始， 每趟倍增： n/4, n/8……直到1

算法分析

• 每趟都使得列表更加接近有序， 这过程会减少很多原先需要的“无效”比对。
• 对谢尔排序的详尽分析比较复杂，大致说是介于O(n)和O(n²)之间
• 时间复杂度约$O(n^{3\over2})$

代码

def shellSort(alist):
    sublistcount = len(alist)//2
    while sublistcount > 0:
        for startposition in range(sublistcount):
            gapInsertionSort(alist, startposition, sublistcount)
        print("After increments of size", sublistcount, "The list is", alist)
        sublistcount //= 2

def gapInsertionSort(alist, start, gap):
    for i in range(start+gap, len(alist), gap):
        currentvalue = alist[i]
        position = i

        while position > gap and alist[position-gap] > currentvalue:
            alist[position] = alist[position-gap]
            position -= gap
        alist[position] = currentvalue

if __name__ == "__main__":
    alist = [54, 26, 93, 17, 77, 31, 44, 55]
    print("origin:",alist)
    shellSort(alist)
    print(alist)

>>>
origin: [54, 26, 93, 17, 77, 31, 44, 55]
After increments of size 4 The list is [54, 26, 44, 17, 77, 31, 93, 55]
After increments of size 2 The list is [54, 17, 44, 26, 77, 31, 93, 55]
After increments of size 1 The list is [54, 17, 26, 31, 44, 55, 77, 93]
[54, 17, 26, 31, 44, 55, 77, 93]

---

归并排序 O(nlogn)—— mergeSort

定义

• 采用分治策略
• 归并排序是递归算法， 思路是将数据表持续分裂为两半， 对两半分别进行归并排序
  • 递归的基本结束条件是：数据表仅有1个数据项，自然是排好序的；
  • 缩小规模：将数据表分裂为相等的两半，规模减为原来的二分之一；
  • 调用自身：将两半分别调用自身排序，然后将分别排好序的两半进行归并，得到排好序的数据表

算法分析

• 将归并排序分为两个过程来分析： 分裂和归并
• 分裂的过程， 借鉴二分查找中的分析结果， 是对数复杂度， 时间复杂度为O(log n)
• 归并的过程， 相对于分裂的每个部分， 其所有数据项都会被比较和放置一次， 所以是线性复杂度， 其时间复杂度是O(n)
• 使用了额外1倍的存储空间用于归并

代码

• 基础版

def mergeSort(alist):
    print("Splitting", alist)
    if len(alist) > 1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i = j = k = 0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k] = lefthalf[i]
                i += 1
            else:
                alist[k] = righthalf[j]
                j += 1
						k += 1

        while i < len(lefthalf):
            alist[k] = lefthalf[i]
            i += 1
            k += 1

        while j < len(righthalf):
            alist[k] = righthalf[j]
            j += 1
            k += 1
    print("Merging", alist)

if __name__ == "__main__":
    alist = [54, 26, 93, 17, 77, 31, 44, 55]
    mergeSort(alist)

>>>
Splitting [54, 26, 93, 17, 77, 31, 44, 55]
Splitting [54, 26, 93, 17]
Splitting [54, 26]
Splitting [54]
Merging [54]
Splitting [26]
Merging [26]
Merging [26, 54]
Splitting [93, 17]
Splitting [93]
Merging [93]
Splitting [17]
Merging [17]
Merging [17, 93]
Merging [17, 26, 54, 93]
Splitting [77, 31, 44, 55]
Splitting [77, 31]
Splitting [77]
Merging [77]
Splitting [31]
Merging [31]
Merging [31, 77]
Splitting [44, 55]
Splitting [44]
Merging [44]
Splitting [55]
Merging [55]
Merging [44, 55]
Merging [31, 44, 55, 77]
Merging [17, 26, 31, 44, 54, 55, 77, 93]
[17, 26, 31, 44, 54, 55, 77, 93]

• 美化版

def merge_sort(lst):
    # 递归结束条件
    if len(lst) <= 1:
        return lst

    # 分解问题，并递归调用
    middle = len(lst)//2
    left=merge_sort(lst[:middle])
    right=merge_sort(lst[middle:])

    # 合并左右半部，完成排序
    merged=[]
    while left and right:
        if left[0]<=right[0]:
            merged.append(left.pop(0))
        else:
            merged.append(right.pop(0))
    merged.extend(right if right else left)
    return merged

if __name__ == "__main__":
    alist = [54, 26, 93, 17, 77, 31, 44, 55]
    print(merge_sort(alist))

---

快速排序

定义

• 和归并排序一样，快速排序也采用分治策略，但不使用额外的存储空间。
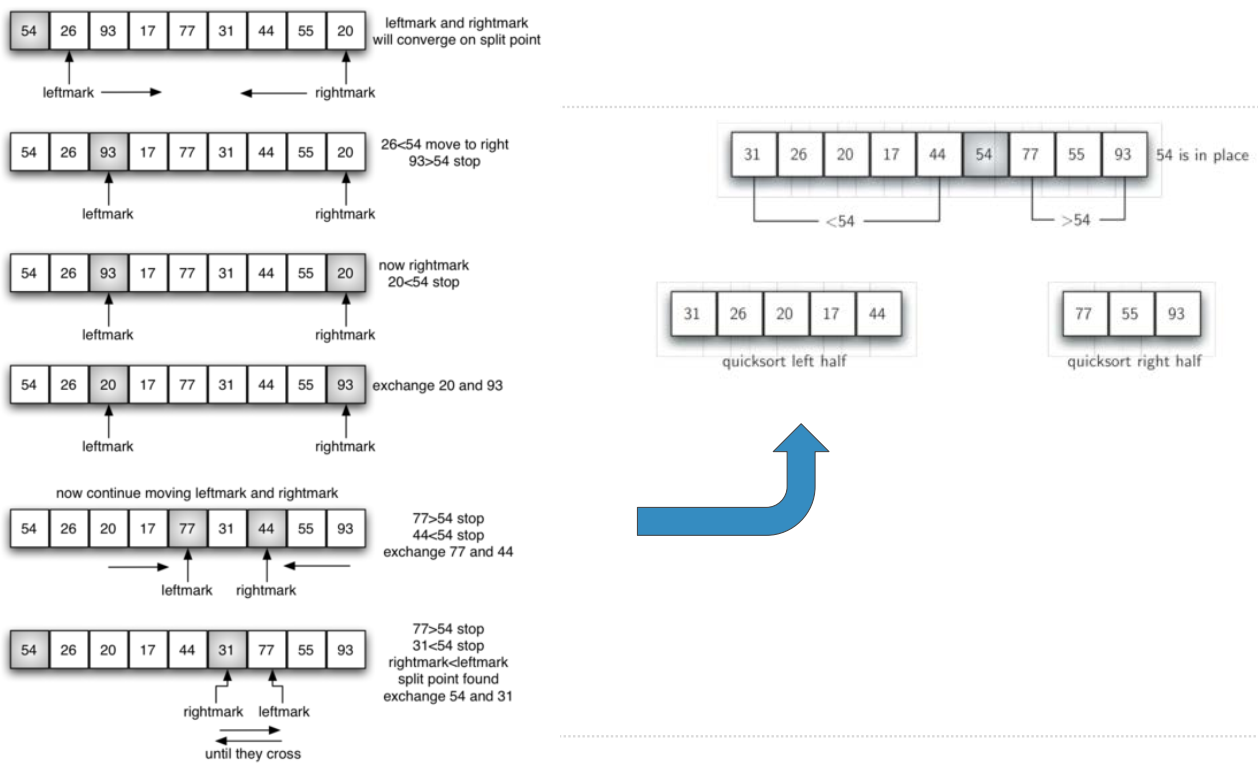
• 快速排序的思路是依据一个“中值”数据项来把数据表分为两半：小于中值的一半和大于中值的一半，然后每部分分别进行快速排序（递归）
  • 如果希望这两半拥有相等数量的数据项，则应该找到数据表的“中位数”
  • 但找中位数需要计算开销！要想没有开销，只能随意找一个数来充当“中值”比如，第1个数。
• 快速排序的递归算法“递归三要素”如下
  • 基本结束条件：数据表仅有1个数据项，自然是排好序的
  • 缩小规模：根据“中值”， 将数据表分为两半， 最好情况是相等规模的两半
  • 调用自身：将两半分别调用自身进行排序（排序基本操作在分裂过程中）

算法分析

• 快速排序过程分为两部分： 分裂和移动
  • 如果分裂总能把数据表分为相等的两部分，那么就是O(log n)的复杂度；
  • 而移动需要将每项都与中值进行比对，还是O(n)
• 综合起来就是O(nlog n)；
• 算法运行过程中不需要额外的存储空间
• 极端情况， 有一部分始终没有数据， 这样时间复杂度就退化到O(n²)
• 可以适当改进下中值的选取方法， 让中值更具有代表性
  • 比如“三点取样”，从数据表的头、尾、中间选出中值

代码

def quickSort(alist):
    quickSortHelper(alist, 0, len(alist)-1)

def quickSortHelper(alist, first, last):
    if first < last:
        # 分裂
        splitpoint = partition(alist, first, last)
        # print(alist)
        # 递归调用
        quickSortHelper(alist, first, splitpoint-1)
        quickSortHelper(alist, splitpoint+1, last)

def partition(alist, first, last):
    # 选定中值
    pivotvalue = alist[first]

    # 左右标初值
    leftmark = first+1
    rightmark = last

    done = False
    while not done:
        # 左标右移
        while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
            leftmark += 1
        # 右标左移
        while rightmark >= leftmark and alist[rightmark] >= pivotvalue:
            rightmark -= 1
        # 两标相错结束循环
        if rightmark < leftmark:
            done = True
        # 左右标的值交换
        else:
            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
    # 中值交换
    alist[first], alist[rightmark] = alist[rightmark], alist[first]
    # 返回中值下标
    return rightmark

if __name__ == "__main__":
    alist = [54, 26, 93, 17, 77, 31, 44, 55]
    quickSort(alist)
    print(alist)

---

算法选择

• 冒泡排序改进：短路
  • 优势高度依赖于数据的初始布局
  • random.shuffle打乱使短路完全失效，还要付出判断、赋值代价，比原始冒泡算法慢了不少
• 排序算法有时候并不存在绝对的优劣， 尤其是时间复杂度相同的算法们
• 要在特定的应用场合取得最高排序性能的话， 还需要对数据本身进行分析， 针对数据的特性来选择相应排序算法
• 除了时间复杂度， 有时候空间复杂度也是需要考虑的关键因素
  • 归并排序时间复杂度O(nlog n)，但需要额外一倍的存储空间
  • 快速排序时间复杂度最好的情况是O(nlog n)，而且不需要额外存储空间，但“中值”的选择又成为性能的关键，选择不好的话，极端情况性能甚至低于冒泡排序
• 算法选择不是一个绝对的优劣判断， 需要综合考虑各方面的因素
  包括运行环境要求、处理数据对象的特性