分组密码(一) — 密码学复习(四)
讲完古典密码之后,接下来将介绍现代密码。
引入
古典密码——对称密码算法的雏形
古典密码的特色:
① 共享同一个密钥:加解密密钥相同,或者由加密密钥很容易得到解密密钥。
② 信息的“搅拌”:搅乱明文26各字母信息,使得明文、密文、密钥之间的统计关系变的混乱。
现代对称密码算法设计核心
现代对称密码体制的加解密算法是可以公开的,只要密钥不泄露就行。现代对称密码又可以分为分组密码和序列(流)密码。下面主要是对分组密码进行介绍。
4.1 分组密码
分组密码的定义:
分组密码是将明文数据序列按照固定长度进行分组,让后在同一密钥控制下用同一算法逐组进行加密,从而将各个明文分组变成一个长度固定的密文分组的密码。
分组密码的主要特点:
同一密钥
同一加密算法
分组加密
分组长度固定
加密:ci=E(mi),i=1,2,...,c=c1c2...,m=m1m2...
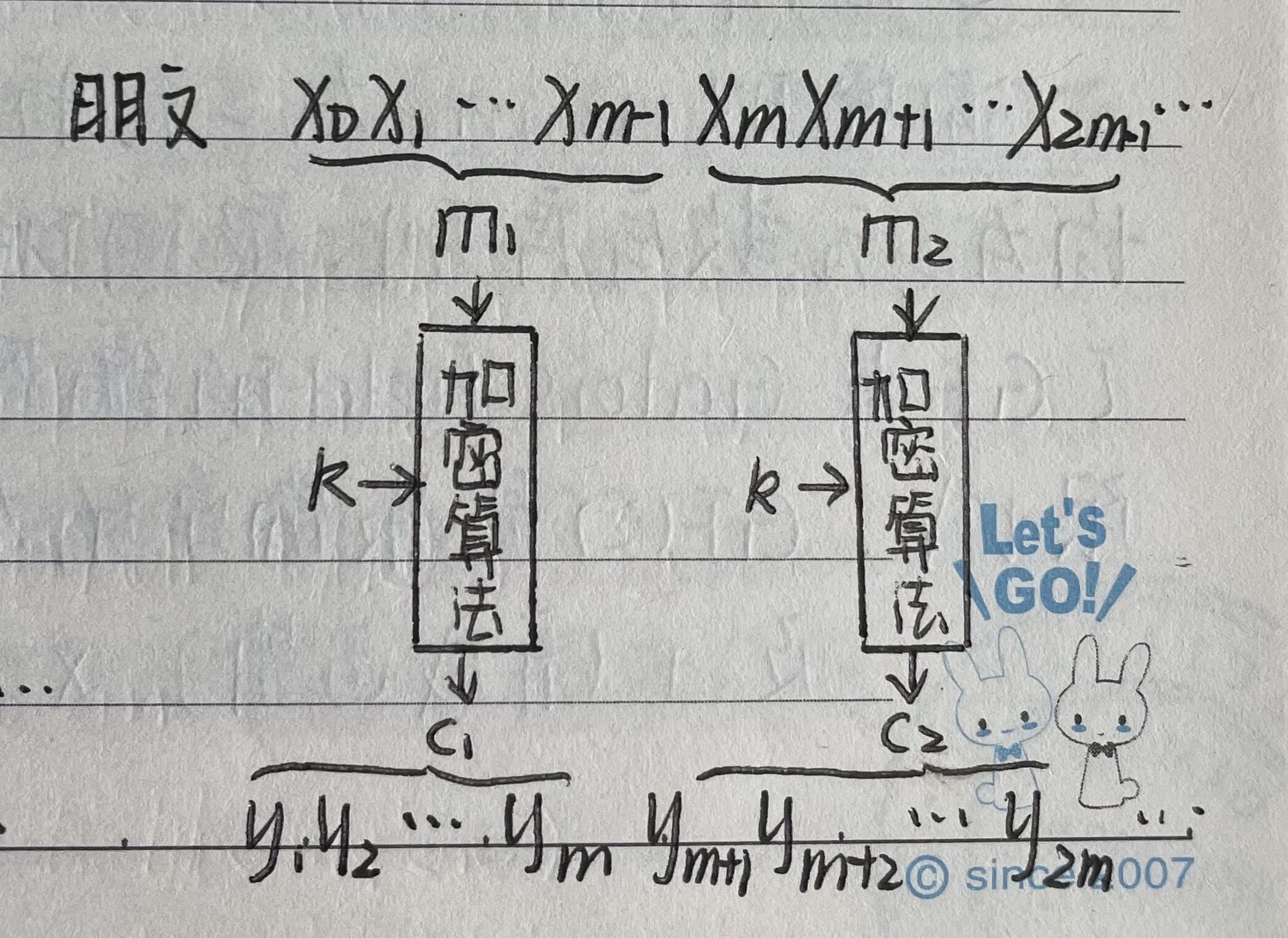
分组密码的数学描述:
将明文消息分组,逐组加密。
将明文消息编码表示后的数学序列x0,x1,...,xi,...划分成长为n的组x=(x0,x1,...,xn-1).
各组(长为n的矢量)分别在密钥k=(k0,k1,...,kt-1).控制变换成输出序列y=(y0,y1,...,ym-1)(长为m的矢量)。
其加密函数E:Vn×K->Vm,Vn和Vm分别是n维和m维矢量空间,K为密钥空间。

明文分组长度为n,密文分组长度为m.
① 若n>m,则称其为有数据压缩的分组密码。
② 若n<m,则称其为有数据扩展的分组密码。
通常取n=m,在二元情况下,明文x和密文y均为二元数字序列。它们的每个分量xi,yi∈GF(2).
常用的分组密码算法:
国际一些现行的标准:DES、3DES、IDEA、AES
中国分组密码算法标准(国密算法、商用算法):SM4
分组密码设计原则:
① 安全原则
安全性是分组密码设计时应考虑的最重要因素,人们一般将Shannon提出的混淆原则和扩散原则作为保证分组密码安全性的两个基本设计原则。
② 实现原则
硬件实现原则 & 软件实现原则
“雪崩效应”
在密码学中雪崩效应是指加密算法(尤其是块密码和加密散列函数)的一种理想属性。
雪崩效应是指当输入发生最微小的改变(例如:反转一个二进制位)时,也会导致输出的不可区分性改变(输出中每个二进制位50%的概率发生反转)。
合格块密码中,无论密钥或明文的任何细微变化都必须引起密文的不可区分性改变。
目的是抗击敌手对密码系统的统计分析。
扩散的实现方法
扩散:就是将明文的统计特性分布到密文中去。
实现方式是使得明文的每一位影响密文中多位的值,等价于说密文中每一位均受明文中多位影响。这时明文的统计特性将被散布到密文中。
因而每一字母在密文中出现的频率比在明文中出现的频率更接近于相等,双字母及多字母出现的频率也更接近于相等。
在二元分组密码中,可对数据重复执行某个置换,再对这一置换作用于某一函数(代换),可获得扩散。(置换+代换)
扩散的目的:使明文和密文之间的统计关系变得尽可能复杂,以使敌手无法得到密钥。
混淆的实现方法
混淆:是是密文和密钥之间的统计关系变得尽可能复杂,以使敌手无法得到密钥。
即使敌手能得到密文的一些统计关系,由于密钥和密文之间的统计关系复杂化,敌手也无法获得密钥。
使用复杂的代换算法可以得到预期的混淆效果。简单的线性代换函数得到的混淆效果则不够理想,一般采用非线性代换。
扩散和混淆成功地实现分组密码本质属性,因而成为设计现代分组密码的基础。
分组密码的设计方法
① 乘积密码 ② 迭代密码
① 乘积密码
Shannon提出乘积密码的思想。乘积密码的基本思想是:通过将一个易于实现的具有一定混乱和扩散结构的较弱的密码函数进行多次迭代来产生一个强的密码函数。
主要思想:通过简单密码的乘积来组合密码体制。

(1)乘法密码
设M=C=Z26,K={a∈Z26;gcd(a,26)=1},对于a∈K,明文x,密文y,定义:
Ea(x)=ax (mod 26)
Da(y)=a-1y (mod 26)
(2)移位密码
对于k∈K,明文x,密文y,定义:
Ek(x)=(x+k) (mod 26)
Dk(y)=(y-k) (mod 26)
假设S1是乘法密码,S2是移位密码,很容易看出S1×S2是仿射密码。
对于S1×S2,其密钥形式为(a,k)
E(a,k)(x)=(ax+k) (mod 26)
对于S2×S1,其密钥形式为(k,a)
E(k,a)(x)=(ax+ak) (mod 26)
② 迭代密码
当今大多数分组密码都是乘积密码,乘积密码通常伴随一系列置换与代替操作,常见的乘积密码是迭代密码。
迭代密码通过讲一个弱的密码函数(称为圈函数、轮函数等)迭代若干次,产生一个强的密码函数,既能快速、有效地实现,又能使明文和密钥得到必要的混淆和扩散。
g称为圈变换、圈函数或轮函数。Nr称为迭代次数、圈数或轮数。(K1,K2,...,KNr)是r个圈子秘钥。
在设计圈函数时,要充分利用代换密码和置换密码各自的优点,抵消各自的缺点,保证通过多次迭代,形成一个强的分组密码算法。

典型的迭代密码:
明确定义一个轮函数和一个密钥编排方案,一个明文的加密将通过Nr轮类似过程。
K——确定长度的随机二元密钥
用K生成Nr个轮密钥(也称为子密钥)K1,K2,...,KNr,其列表(K1,K2,...,KNr)即为密钥编排方案,它是由K经过一个固定的、公开的算法生成的。
轮函数g
轮函数g以轮密钥Kr和当前状态Wr-1作为它的两个输入,下一个状态定义为Wr,初态W0被定义为明文x,密文y定义为经过Nr轮后的状态。有
Wr=g(Wr-1,Kr)
加密过程:
W0 <- x 初态
W1 <- g(W0,K1) 第1轮
W2 <- g(W1,K2) 第2轮
...
WNr-1 <- g(WNr-2,KNr-1) 第Nr-2轮
WNr <- g(WNr-1,KNr) 第Nr-1轮
y <- WNr 第Nr轮
为解密,g在第二个变量固定的情况下,必须是单射,即等价于存在g-1,g-1(g(w,k),k)=w.
解密过程:
WNr <- y
WNr-1 <- g-1(WNr,KNr)
...
W1 <- g-1(W2,K2)
W0 <- g-1(W1,K1)
x <- W0
迭代密码常见的模型有S-P网络(代替-置换网络),Feistel网络等。
代替-置换网络(S-PN)Substitution-Permutation
一个S-PN就是一类特殊的迭代密码,设l和m都是正整数,明密文都是长为lm的二元向量。一个S-PN包含两个变换,分别记为∏s和∏p.
∏s:{0,1}l -> {0,1}l 实现l比特的代替,即S盒。
∏p:{1,2,...,lm} -> {1,2,...,lm},实现lm比特的置换,即P盒。
x=(x1,x2,...,xm)=x<1>||x<2>||...||x<m>.
x<i>=(x(i-1)l+1,x(i-1)l+2,...,xil),1≤i≤m.
S-PN特点:
由Nr轮组成,在每一轮(最后一轮稍有不同),先用异或操作混入该轮的轮密钥,再用∏s进行m次代换,然后用∏p进行一次置换。
密码体制 3.1 代换-置换网络

算法 3.1

① 对密钥编排方案适当修改并用S盒的逆代替S盒,该算法也能用于解密。
② 第一个和最后一个异或轮密钥(白化)使得一个不知道密钥的攻击者,无法开始进行一个加密或解密操作。

非线性替换S一般称为混乱层,主要起混乱的作用;线性置换P一般称为扩散层,主要起扩散的作用。
优点:
① 结构清晰、容易分析和把握每层密码学指标,从而把握密码学的安全性;
② 扩散较Feistel结构快。
缺点:
不容易得到对合的密码算法。
Fristel体制
① 单轮Feistel
Feistel模型将输入(2w位)分成相同长度的两部分Li和Ri,按如下方式进行变换。
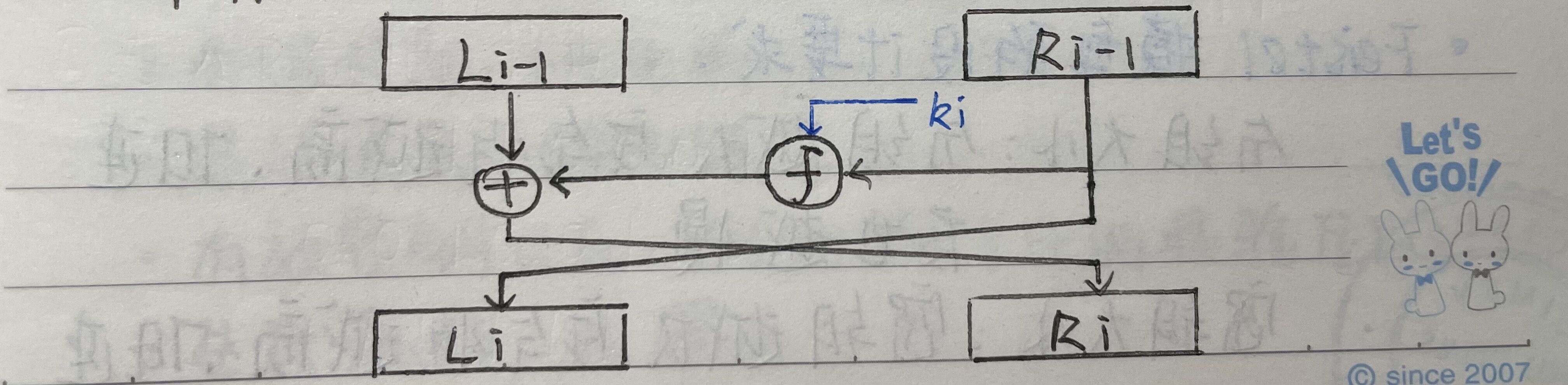
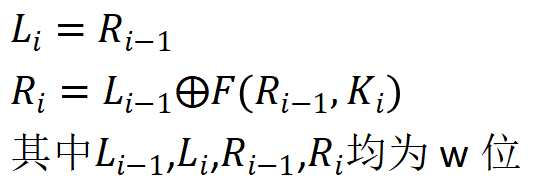
② Feistel模型的特点
(1)每轮的输入(明文分组或上轮的输出)被分成左右两半;
(2)右边一半数据直接作为输出的左边一半;
(3)输出的右边一半由输入的左边一半异或右边一半输入在一个函数F作用下的结果而得到的;
(4)F函数是轮变换的核心,它被称为轮函数。轮函数F有两个输入:本轮的右边一半输入和本轮的轮(子)密钥;
(5)轮函数F得到结构式固定不变的,这是各轮的输入不断变化;
(6)轮函数中包含了代换、置换以及换入子密钥的操作;
(7)加解密算法的结构相同,只是子密钥的使用出相反。
③ Feistel模型的设计要求
分组大小:
分组越大,安全性越高,但速度也就越慢。
密钥大小:
密钥越长,安全性越高,但速度也就越慢。
循环次数:
循环越多,安全性越高。
圈函数:
复杂性越高则抗击密码分析的能力就越强。
子密钥产生算法:
复杂性越高,则密码分析的难度就越大。
此外还要考虑算法的执行速度,设计算法便于分析。
④ 优点:
(1)不管f是什么函数,基本函数都可逆,进而确保轮函数可逆以及整个密码算法可逆;
(2)由于基本函数是对合的,进而确保轮函数是对合的,以及整个密码算法是对合的。
这使得密码算法的设计变得比较容易。
⑤ 缺点:
扩散速度慢,算法迭代2轮才能改变输入的每一位。



