古典密码的演化 (二)— 密码学复习(三)
前面介绍了几种古典密码算法(凯撒密码、仿射密码、维吉尼亚密码、希尔密码、置换密码),下面将对其中的几种密码算法站在攻击者的角度进行分析。
三、密码破译
密码破译的原则:遵循观察和经验
方法:采用归纳与演绎
步骤:分析、假设、推测和证实
三大要素:
① 语言频率特征:如E出现频率最高;
② 连接特征:q...u,Iex.
③ 重复特征:th,tion,tious.
3.1 单表代换——密码分析
利用统计数据获得密码分析。
例:假设从仿射密码获得的密文为:
FMXVEDKAPHFERBNDKRXRSREFMORUDSDKDVSHVUFEDKAPRKDLYEVLRHHRH.
通过上面的57个密文字母,就可以分析仿射密码。
最高频率的密文字母:
R——8次 D——7次 E、H、K——各5次 F、S、V——各4次
根据已知的26个英文字母的概率分布表:
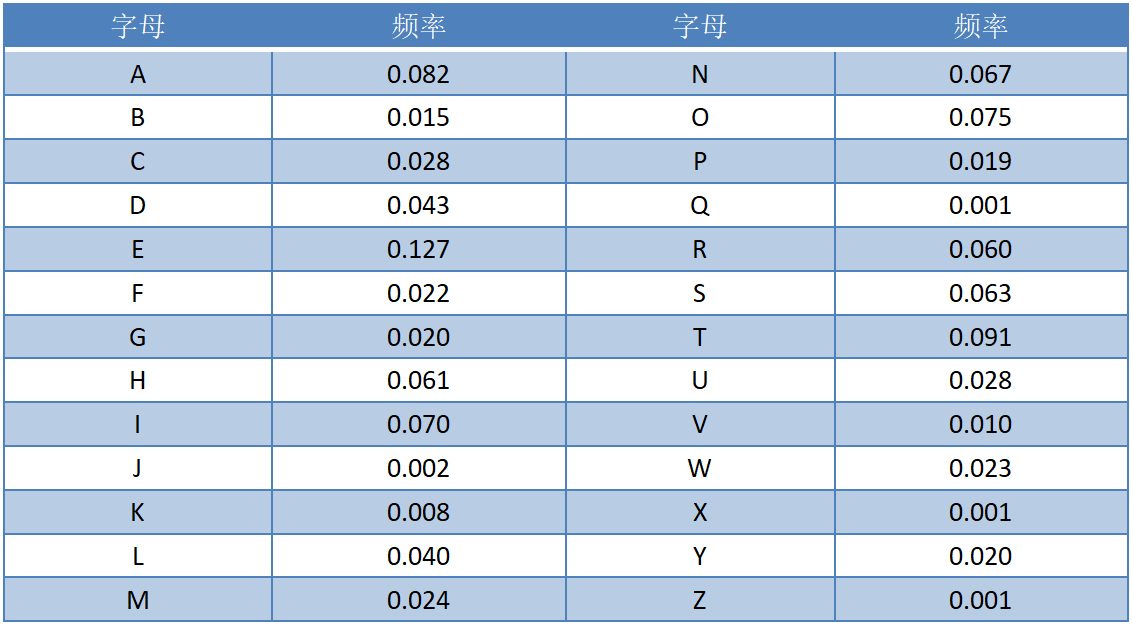
E——0.127 T——0.091 A——0.082 O——0.075
① 假定R是E的加密,D是T的加密
数值化后有:ek(4)=17 dk(19)=3
而加密函数 ek(x)=ax+b.
可以得到两个包含两个未知数的线性方程组:
4a+b=17
19a+b=3
解得 a=6,b=19 (mod 26)
这是一个非法密钥,因为gcd(6,26)=2≠1,所以假设不成立。
② 假设R是e的加密,E是t的加密,解得 a=13,gcd(a,26)=13≠1,故此时假设不成立。
③ 假设R是e的加密,K是t的加密,此时解得 a=3,b=5.至少这是一个合法密钥。
接着计算k=(3,5)时的解密函数,之后对密文进行解密,观察的到的明文是否有意义。
容易验证a=3,b=5是一个有效密钥,解得明文为:
Algorithms are quite general definitions of arithmetic process.
3.2 多表代换——密码分析
3.2.1 希尔密码
对希尔密码进行已知明文分析。
希尔密码在唯密文攻击下是很难破解的,但容易被已知明文攻击所攻破。
假设确定了m的值,且得到至少m对不同的m元组:
xj=(x1j,x2j,...,xmj),
yj=(y1j,y2j,...,ymj).(1≤j≤m)
已知yj=ek(xj).
如果定义两个m×m矩阵,X=(),Y=(),则有矩阵方程Y=Xk,k是未知密钥。
例:

3.2.2 维吉尼亚密码
分析维吉尼亚密码的方法:
第一步:确定密钥字的长度m:
① Kasiski测试法
② 重合指数法(Coincidence Index)
...
第二步:确定密钥的具体内容
交互重合指数法、拟重合指数方法
第三步:用单表代换密码的解密方法解密
统计分析方法
下面将对涉及到的各种方法进行简单的介绍。
(1)Kasiski测试法
相同的字母序列可能出现在明文的不同地方,这些重复模式是有趣的。因为他们提供了文本里周期的信息。
例子:
明文:REQUESTS ADDITIONAL TEST
密钥:TELEXTEL EXTELEXTEL EXTE
密文:CAVKTBLT EUQWSQIGEA LTBL
反映了序列EST间隔的字母数(15)为密钥长度(5)的倍数。
若用给定的m个密钥表周期地对明文字母加密,则当明文中有两个相同字母组在明文序列中间隔的字母数为m的倍数时,这两个明文字母组对应的密文字母组必相同。
反过来,若密文中出现两个相同的字母组,它们所对应的明文字母组未必相同,但相同的可能性很大。
如果将密文中相同的字母组找出来,并对其相同的字母数综合研究,找出它们的相同字母数的最大公因子,就有可能提取出有关密钥字的长度m的信息。
寻找密文中相同的片段时,计算每对相同密文片段对之间的聚类,不妨记为d1,d2,...,di,若令密钥字的长度为m,则m=gcd(d1,d2,...,di).
例子:
明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
密钥:ABCDEF AB CDEFA BCD EFABCDEFABCD
密文:CSASXT IT UKSWT GQU GWYQVRKWAQJB
此时,明文中重复的元素在密文中并不重复。
若将密钥长度6变成4位(ABCDEF->ABCD),得到的密文有:
CSASTP KV SIQUT GQU CSASTPIUAQJB
此时,卡西斯基试验就能产生效果,对于更长的段落基于此方法更为有效。因为密文中重复的片段很多(退出情况下)。如通过下面的密文就能破译出密钥长度:
密文:DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
其中,两个DYDUXRMH的出现相隔了18个字母,因此可以假定密钥的长度是18的约数,即长度为18、9、6、3或2.而两个NQD则相距20个字母,意味着密钥的长度应为20、10、5、4或2.取两者的交集,则可以基本确定密钥的长度为2.
(2)重合指数法 Coincidence Index
我们可以通过别的参数来描述猜测的密钥长度m是否准确的。当计算某个密文的重合指数(重合概率 Index of Coincidence)时,即相当于求在某个密文中随机无放回地抽取其中的两位,这两位的字母相同的概率。
定义一 设X=x1x2...xn是一个长度为n的英文字母串,则X中任意选取两个字母相同的概率定义为重合指数,用IC(X)表示。
设y是一个长度为n的密文,即y=y1y2...yn,其中yi是密文字母,同样来求从中抽取两个字母相同的概率是多少?
设NA为字母A在这份密文中的频数,NB为字母B在这份密文中的频数,以此类推。
从n个密文字母中任意抽取两个有:
![]()
NA个A组成的一对A有:
![]()
从y中抽到两个字母都为A的概率有:
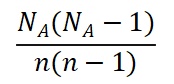
从y中抽到两个相同字母的概率为:
![]()
这个数据称为这份密文的重合指数,记为IC(Y).
假设X是英文文献,根据字母A,B,...,Z出现的期望概率P0,P1,...,P25,这两个字母都为A,B,...,Z的概率为P02,P12,...,P252.那么,
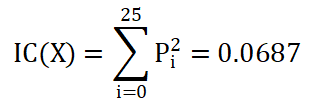
若对随机产生的英文字母序列进行讨论,那么此时每个英文字母出现的期望概率均为1/26,则在Y中任意抽取两个字母相同的概率为
![]()
那么,
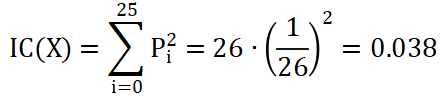
假设我们使用维吉尼亚加密的密文串为Y,将串分割成m个长度相等的子串,分别为Y1,Y2,...,Ym.
这样可以以列的形式写出密文,构造出一个m×(n/m)的矩阵。矩阵的每一行对应于子串Yi,1≤i≤m.
如果按照上述方法构造,则m实际上就是密钥字的长度,使得每行都是单表代换加密的,不同行是由不同的密钥加密的。于是每一行的重合指数IC(Yi)=0.0687.
另一方面,如果m不是密钥长度,那么子串Yi看起来更随机,因为它们是通过不同密钥以移位加密方式获得的。随机串的重合指数为IC(Y)=0.0385.
0.0687和0.0385差距还是较大的,故可以按这种方法确定密钥字长度。
下面来用一个具体的例子进行分析。
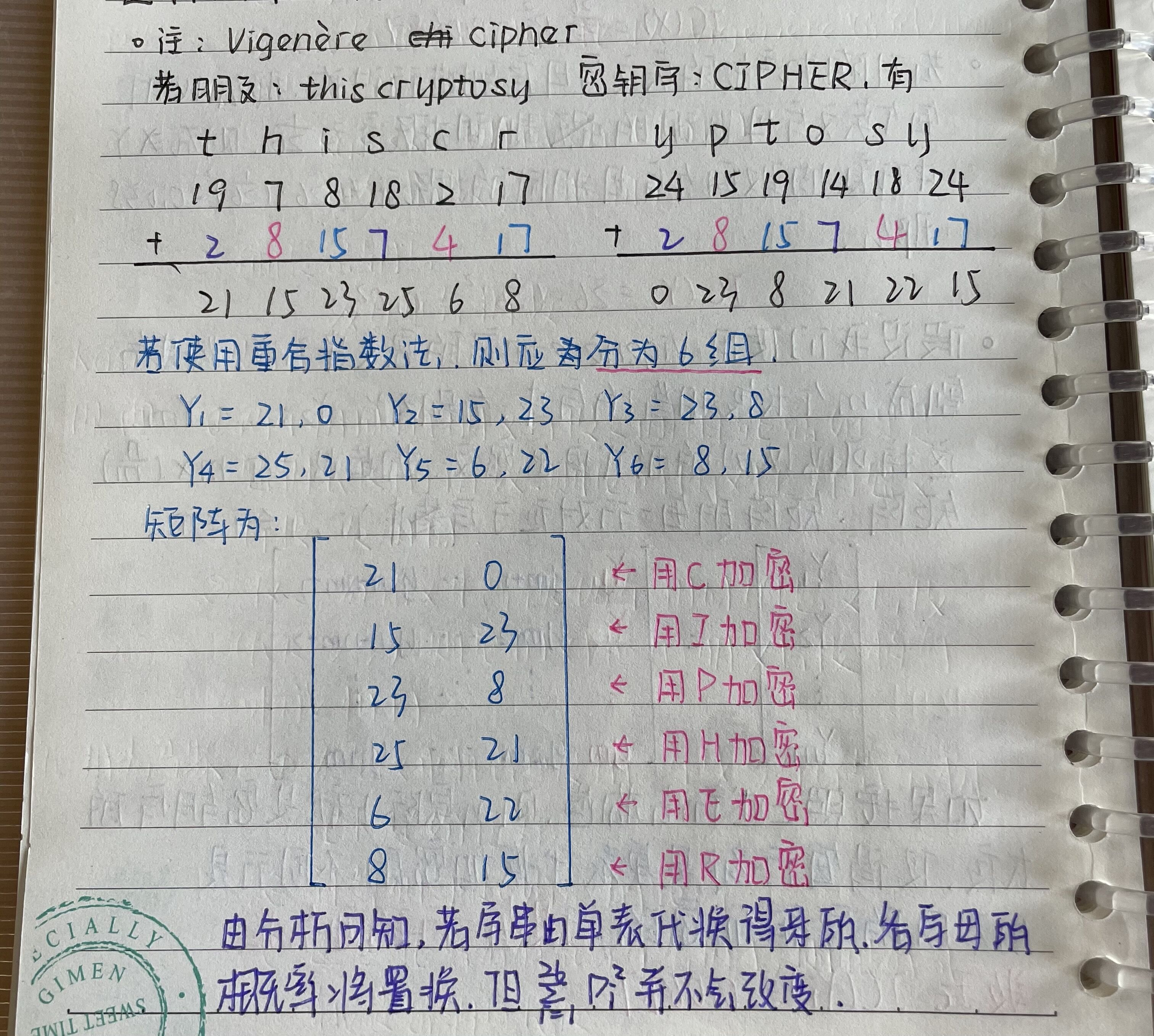
所以,若分组准则m为密钥长度,那么IC(Y)=0.0687,若不为密钥长度,此时每行都是由多个不同字母得来的,重合指数为0.0385.
下面用一个经过维吉尼亚加密后的密文来举例。(①Kasiski测试法 ②重合指数法)


总结:
1.确定密钥字长度
Kasiski测试法 (估计)
重合指数法 (验证)
2.确定密钥字
交互重合指数
(1)Kasiski测试法
原理:
① 两个相同的明文片段之间的距离如果是密钥长度的倍数,则它们所对应的密文片段一定相同。
② 反之,若密文中出现两个相同的密文片段(长度>3),则它们对应的明文片段极有可能相同,
应用步骤:
① 在密文中标出重复的三个或多个字符结构,记下起始位置。
② 计算相邻起始点的距离。
③ 这些距离若存在某个公因子,则很有可能是密钥字长度。
(2)确定密钥字长度——重合指数法
原理:
① 通过比较字符串与自然语言之间的相似性。
② 如果密文序列是使用单表加密得到的,那么它的重合指数与自然语言的重合指数近似相等。
③ 否则,它的重合指数与随机分布的重合指数近似相等。
通过计算IC(Y)一般能确定密钥长度,或验证由Kasiski测试法得到的长度是否正确。



