古典密码的演化 （一）— 密码学复习（二）

  复习完密码学的基本概念后，下面对古典密码进行简单的复习。下图列出的是经典密码体制的框图。（由于比较懒就直接放笔记的照片了⁄(⁄ ⁄•⁄ω⁄•⁄ ⁄)⁄）

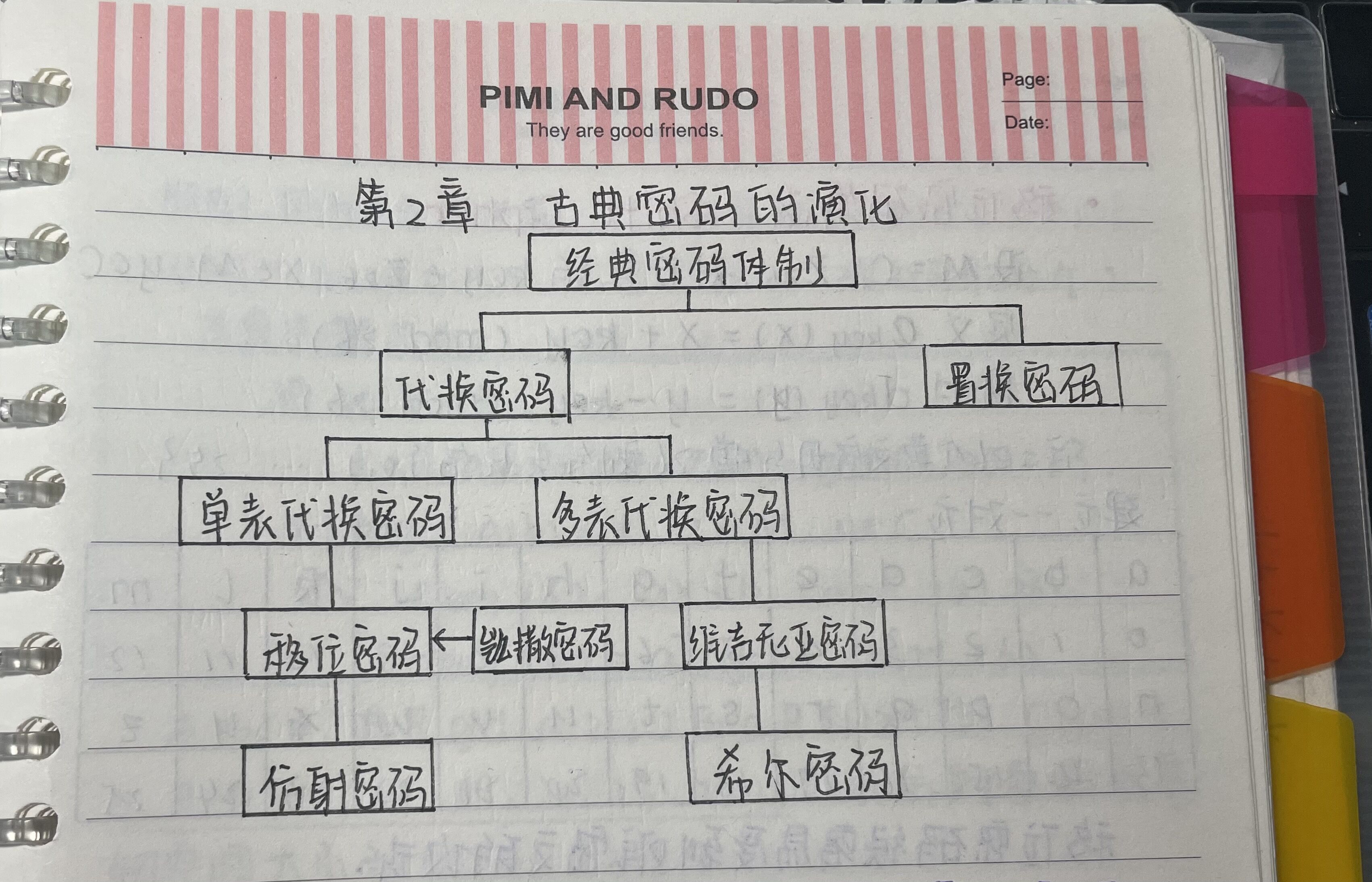
  古典密码学大体上可以分为 代换密码 和 置换密码。

  （1）代换密码

  构造一个或多个密文字母表，然后用密文字母表中的字母或字母组来代替明文字母或字母组。各字母或字母组的相对位置不变，但其本身改变了。

  （2）置换密码

  又称换位密码。把明文中的字母重新排序，字母本身不变，但其位置改变了。

  2.1 移位密码算法 Shift Cipher

  设 M = C = Z₂₆,对任意的 key∈Z₂₆, x∈M, y∈C.

  定义e_key(x) = x + key (mod 26)

  同时d_key(y) = y - key (mod 26)

  注：26个英文字母与模26剩余类集合{0,1,...,25}建立一一对应。

  移位密码很容易受到唯密文的攻击。

  例子：凯撒密码（key = 3）

   若此时明文为venividivici.则密文为：yhqlylglylfl.若解密只需将密文左移三位即可。

  2.2 仿射密码算法

  加密函数取形式为：e(x) = ax + b (mod 26), a,b∈Z₂₆.

  要求唯一解的充要条件是gcd(a,26)=1.

  注：之所以要求a与26互素。目的是为了保证逆元存在。同时，因为a与26互素，所以a可取φ(26)个。φ(26)=φ(2)φ(13)=1×12=12.故a可取12个。

  该算法描述为：

设 M = C = Z₂₆

  K = {(a,b)∈Z₂₆×Z₂₆; gcd(a,26)=1}

对 key=(a,b)∈K, x∈M, y∈C,

定义 e_key(x) = ax + b (mod 26) 和 d_key(y) = a^-1(y-b) (mod 26).

  在Z₂₆中，满足gcd(a,26)=1的a只有12个值(1,3,5,7,9,11,15,17,19,21,23,25),因此仿射密码的密钥空间大小为12×26=312个。

  对于Z₂₆中与26互素的元素，相应的乘法逆元为：

1^-1 mod 26 = 1     3^-1 mod 26 = 9     5^-1 mod 26 = 21   7^-1 mod 26 = 15   

9^-1 mod 26 = 3    11^-1 mod 26 = 19   15^-1 mod 26 = 7    17^-1 mod 26 = 23   

19^-1 mod 26 = 11   21^-1 mod 26 = 5    23^-1 mod 26 = 17   25^-1 mod 26 = 25

  求逆元过程（以9^-1 mod 26 = 3为例）

  9·9^-1≡1 (mod 26)

  9x≡1 (mod 26) 其中x≡9^-1 (mod 26)

  x = x^-1+9^-1·26 (mod 26)

   = 9^-1(1+26)  (mod 26)

   = 3       (mod 26)

 ∴ 9^-1≡3 (mod 26)

  仿射密码算法例子

 设 k=(7,3),注意到7^-1 mod 26 = 15,

  加密函数：e_k(x) = 7x + 3 (mod 26)

  解密函数：d_k(y) = 15(y-3) (mod 26) = 15x-19 (mod 26)

  易见 d_k(e_k(x)) = d_k(7x + 3) = 15(7x + 3)-19 = x+45-19 = x (mod 26)

  若加密明文为hot，则有如下步骤：

  ① 转换字母h、o、t为数字7、14、19

  ② 然后加密：

 

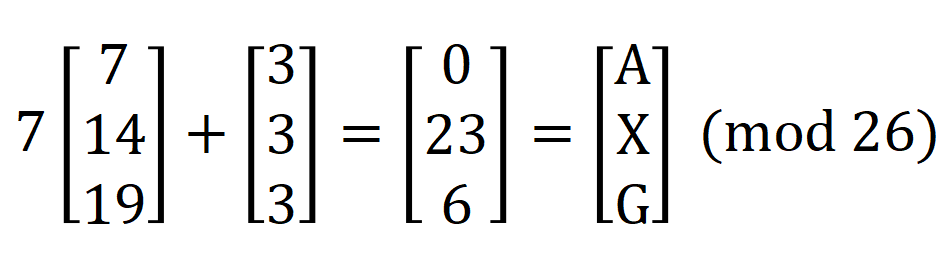
  ③ 解密有：

  2.3 单表代换密码 —— 分析

 （1）密钥量一般比较小，难以抵抗穷尽搜索攻击。

 （2）即使密钥量很大，但因为没有将明文字母的频率隐藏起来，所以也很容易受到频数分析法的攻击。

  2.4 单表代换的优缺点

优点：

  明文字符的形态一般将面目全非。

缺点：

  a.明文的位置不变

  b.明文字符相同，则密文字符也相同。从而导致：

   ① 若明文字符被加密成密文字符a,则明文中e的出现次数就是密文中字符a的出现次数；

   ② 明文的更随关系反映在密文之中。因此，明文字符的统计规律就完全暴露在密文字符的统计规律之中，形态变但位置不变。 

  2.5 单表代换密码的统计分析举例

  密文为：YIFQFMZR...CFWDJNZDIR（共168个字母）

  分析：∵Z出现20次，出现的频率约为0.12

∴猜测D(Z)=e

∵出现至少10次的密文字母为C、D、F、J、M、R、Y,出现频率约在0.06到0.095之间

∴猜测{D(C),D(D),D(F),D(J),D(M),D(R),D(Y)}={t,z,o,i,n,s,h,r}...

以此类推

  不太明白的话可以参考[2.3_单表代替密码的分析]

  2.6 多表代换密码

  多表代换密码是一系列（两个以上）代换表依次对明文消息的字母进行代换的方法。可以分为：非周期多表代换密码 和 周期多表代换密码。

  非周期多表代换密码：代换表是非周期的无限序列。

  周期多表代换密码：代换表个数有限，重复使用。

  2.6.1 维吉尼亚密码 Vigenére cipher

  设 m 是某固定的正整数，定义P=C=K=(Z₂₆)^m,对一个密钥 k=(k₁,k₂,...,k_m),定义

e_k(x₁,x₂,...,x_m) = (x₁+k₁,x₂+k₂,...,x_m+k_m)

d_k(y₁,y₂,...,y_m) = (y₁-k₁,y₂-k₂,...,y_m-k_m)

  且所有的运算都在Z₂₆中。

  简单地说，可以将其描述为如下形式：

密钥 K=(k₁,k₂,...,k_n),

明文 P=(p₁,p₂,...,p_n),

密文 C=(c₁,c₂,...,c_n).

加密：c_i=p_i+k_i (mod 26)

解密：p_i=c_i-k_i (mod 26)

  密钥一般是一个单词或一句话去除后面的重复字母后构成。

  本质：多个移位密码

  密钥量：对于n为密钥，密钥量有

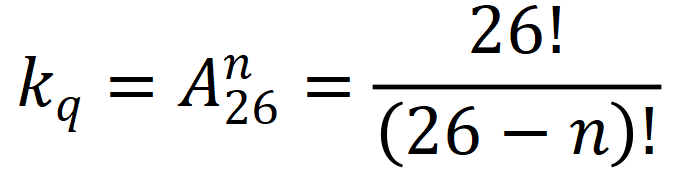  例子:

  2.6.2 希尔密码 Hill cipher

  设m是某个固定的正整数，P=C=(Z₂₆)^m,又设K={m×m可逆阵，Z₂₆};对任意k∈K,定义

e_k(x) = xk

则d_k(y) = yk^-1

  其中所有的运算都是在Z₂₆中进行。

  其中明文、密文和密钥可以写成如下形式：

 

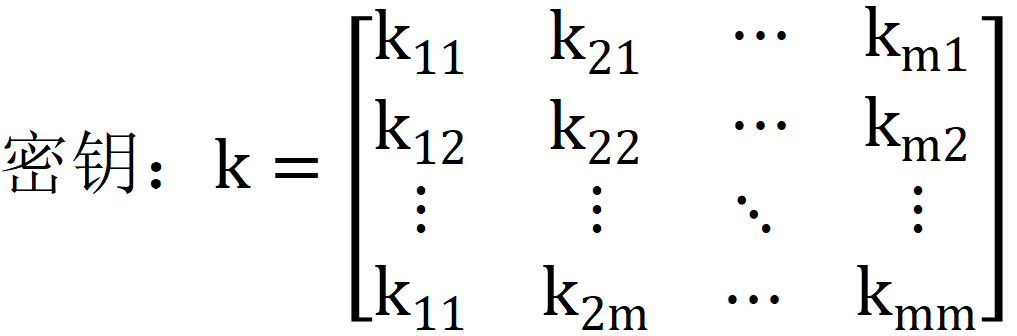
  注意：

    k必须满足条件：

  1.非奇异矩阵，即|k|≠0,

  2.gcd(|k|,26)=1 (mod 26)

  加密：

 

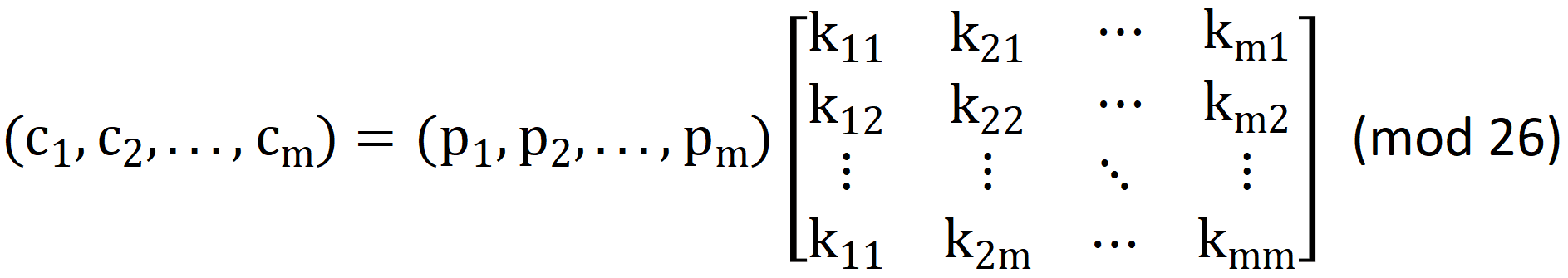
  解密：

 

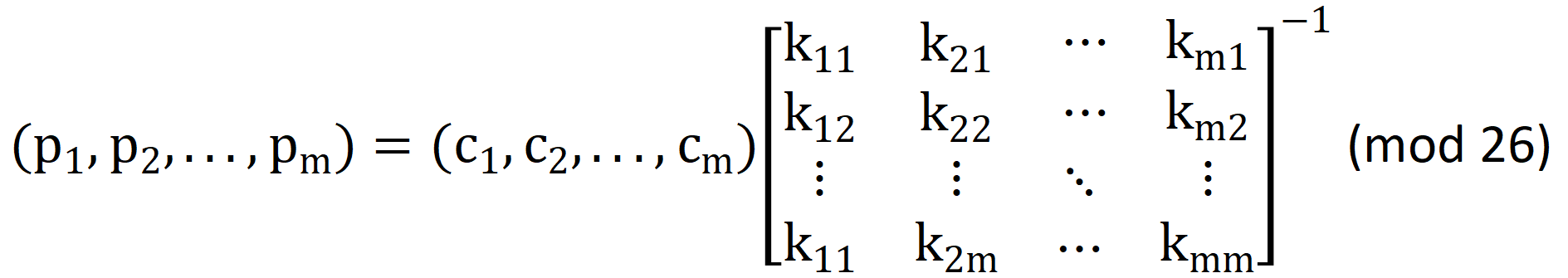
  例子1：

  例子2：

  介绍完希尔密码后，接下来对希尔密码的特点进行介绍：

（1）完全隐藏了单字母的频数；

（2）字母和数字的对应可以改成其他方案，使得更不容易被攻击成功；

（3）能比较好地抵抗频数法的分析，对抗唯密文攻击强度较高。

 

  2.7 置换密码 Permutation Cipher 或 Transposition Cipher

  设m是某个固定的正整数，P=C=(Z₂₆)^m,且K由所有{1,2,...,m}的置换组成，对一个密钥（即一个置换∏），定义

e_∏(x₁,x₂,...,x_m) = (x_∏(1),x_∏(2),...,x_∏(m))

d_∏(y₁,y₂,...,y_m) = (y_∏^-1(1),y_∏^-1(2),...,y_∏^-1(m))

  其中∏^-1是∏的逆置换。

  例子：

  在简单对几种古典密码算法进行介绍后，下一篇将介绍密码破译。