密码学基础概念 — 密码学复习(一)
写在前面:
最近因为疫情,闭关了半个多月准备的事情延期了,也不知道什么时候才能弄。另外的事情又冒出来了,所以只能把可搜索加密先放放,写一下密码学的复习笔记了。但最近写可搜索加密发现还是有人看的,让我十分有动力。忙完这点事情希望可以尽快把可搜索加密更完。
下面就进入今天的正题 —— 密码学基础概念。
在开始介绍之前可以先看看三个有趣的问题:
① 电话抛币协议 这个问题简单描述就是:在没有第三方协助下,通话双方有办法在电话里模拟抛掷一枚公平的硬币吗?
② 百万富翁问题 这个问题简单描述就是:两个百万富翁相比较一下谁更富有,但是不想暴露自己的确切钱数,也不想让第三方知道,要怎么比较呢?
③ 零知识证明问题 这个问题简单描述就是:在不泄露任何有用信息的前提下,向验证者证明自己确实知道某一事情。
关于这些问题其实网上有很多写得很好的文章,在这里我只是给出一个对其简单解释的文章/课件链接,想要深入了解可以自行搜索。
一、基本概念
接下来就对密码学中经常用到的一些字母简单介绍。
M —— 明文空间 C —— 密文空间 K —— 密钥 E —— 加密算法 D —— 解密算法
有E(m)=c;D(c)=m.
一些常见的人物:
Alice:协议发起者 Bob:协议应答者 Eve:窃听者和可能的攻击者 Oscar:被动的观察者,仅仅根据从公开信道获得的资料进行破译 Malice,Mallory:主动的攻击者,可能会拦截数据、篡改信息和冒充合法的通信者。
1.1 基于公开信道的攻击手段
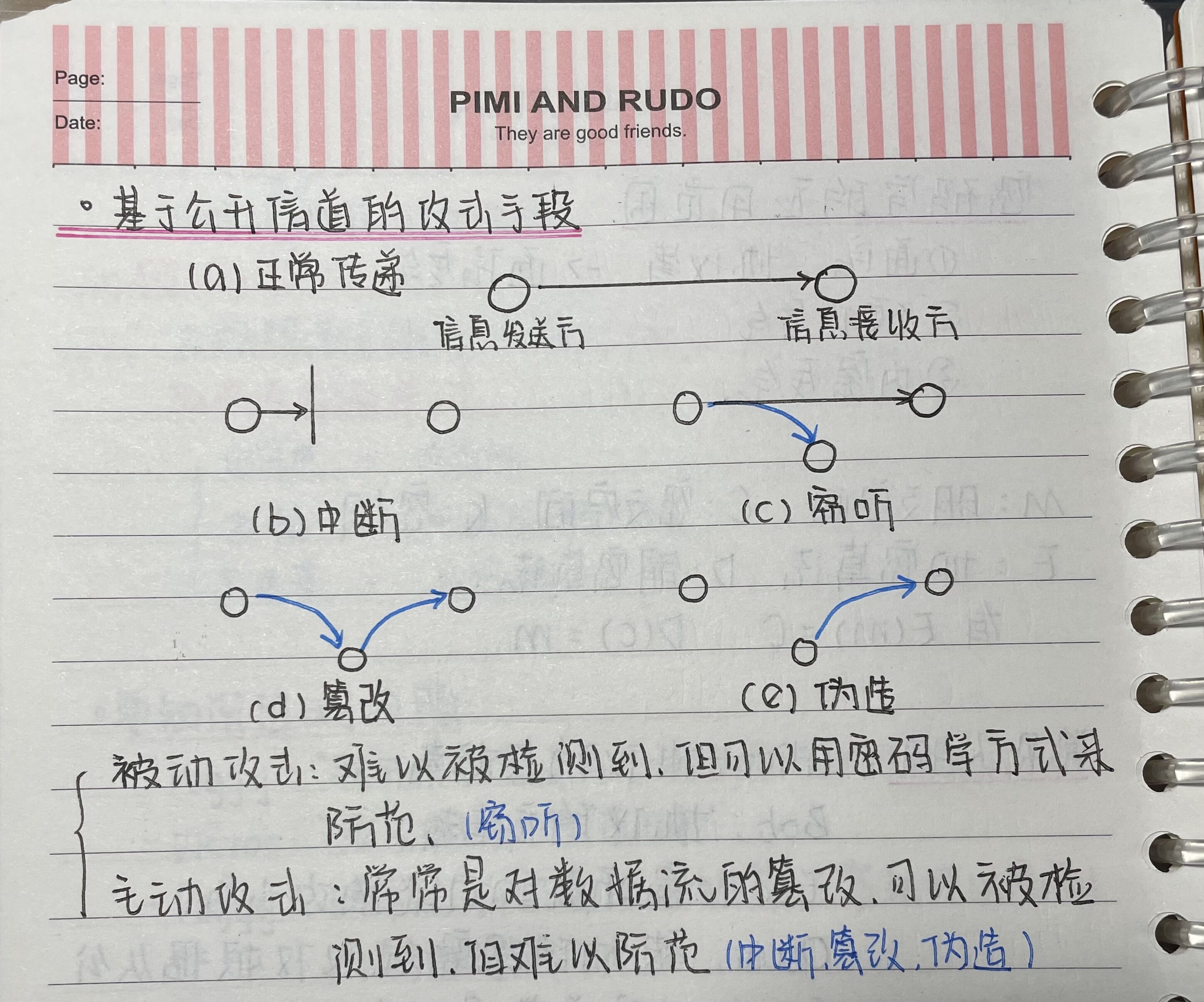 可以看到有;①中断 ②窃听 ③篡改 ④伪造 四种攻击手段。
可以看到有;①中断 ②窃听 ③篡改 ④伪造 四种攻击手段。
攻击又可以分为被动攻击和主动攻击。被动攻击难以被检测到,但可以用密码学方式来防范。主动攻击常常是对数据流的篡改,可以被检测到。
(原谅我比较懒不想在画图了,直接把笔记的图贴上来hhh)
1.2 密码分析的攻击方式
根据攻击所能获得的信息资源,可以将其攻击方式分为六类:
① 唯密文攻击:攻击者有一些消息的密文,这些消息都是用同一加密算法的。攻击者的目的是恢复尽可能多的明文,当然最好是获得消息的加密密钥。
② 已知明文攻击:攻击者在得到密文的同时还知道这些消息的明文。攻击的目标就是根据加密信息推导出用来加密的密钥,或者等价的,即使没有找到密钥但是能找到一种方法,能对同一密钥加密的密文获得其明文。
③ 选择明文攻击: 攻击者不仅可以获得一些密文-明文消息对,而且能选择被加密的明文。这比已知明文攻击更加有效,因为攻击者可以选择能加密的特定明文块去获得密文,那些快可能产生更多密钥消息。
④ 自适应选择明文攻击: 这是比选择明文攻击具有更多权限的攻击方式。攻击者不仅可以选择一大块明文用来加密获得密文,还可以基于以前的结果修正这个选择,选择另一块余地一块明文相关的明文块。
⑤ 选择密文攻击: 攻击者能选择不同的被加密的密文,并可能得到对应的解密的明文。比如,攻击者能选择不同的被加密的密文,并可能得到对应解密的明文。比如,攻击者获得了某个解密机,或者攻击这是在渗透在保密系统内部的员工,可以有一定的权限获得某些密文的原文等。
⑥ 选择密钥攻击: 指密码分析者具有不同的密钥间关系的有关知识。如在类似于差分密码分析的相关密钥分析中有所应用。
1.3 基于密钥的算法
加密和解密算法,根据所使用的密钥的性质,通常分为两类:对称算法和公开密钥算法。在实际使用中,加密和解密的密钥可能有所区分,下面两个式子更精确的描述加解密过程:
y = Ek1(x) (1)
x = Dk2(y) (2)
(1)对称密钥密码算法
加密密钥k1和解密密钥k2相同或相关(k1和k2可以相互推导)。
主要包含 序列算法 和 分组算法。
序列算法:一次只对明文中的单个比特(又是对字节)运算。
分组算法:对明文中一组比特进行运算。
对称密钥密码算法例子:古典加密体制、DES、AES.
(2)非对称密钥面积码算法(公开密钥算法)
加密密钥k1和解密密钥k2之间没有任何关联。在使用中,通常将加密密钥公开,所有人都可以用这个密钥加密,而只有解密密钥的持有者才可以解密。
Alice只要知道Bob的公钥,就可以将自己的消息用Bob的公钥进行加密,然后发送给Bob.对于加密后的消息,只有Bob才能够解密。
例子:RSA.
1.4 密码协议
密码协议是应用密码学,解决实际信息系统中信息安全问题的方式。协议是一系列步骤,它包含双方或多方。设计它的目的是要完成一项任务,协议不同于算法和任务,它具有如下特点:
(1)协议中的参与方都必须了解协议,并预先知道所要完成的所有步骤。
(2)协议中的每个参与方都必须同一并遵守它。
(3)协议必须是清楚的。每一步都必须明确定义。如进行通信或完成一方或者多方运算,并不会引起误解。
(4)协议必须是完整的。对每种情况必须规定具体的动作。
密码协议的主要目标:
密码协议在安全系统中,其关键性目的并不是保证密码算法的不可破译,二是假设密码算法本身是安全的。借助这种安全的密码算法,达到以下四个主要目标:
(1)机密性
搭线窃听者Eve不能读取到信道上的传输的信息的明文,主要的手段是先加密后传输,由接受者解密。
(2)完整性
接收者Bob需要确认Alice的消息没有被更改过。密码学的散列函数,就提供了检测方法来检测数据是否被攻击者有意无意地修改过。
(3)认证性
接收者Bob需要确认消息确实是Alice发送的,而不是冒名顶替的行为。通常这种认证包含两类:实体认证 和 数据源认证。对消息中所涉及参与方的鉴别,也常用身份鉴别来表示。身份认证主要是确认主体是都合法的参与者;数据源认证主要是确认消息是由他所声称的主体生成和发送的。
(4)抗抵赖性
也称为不可否认性。对于一个已经进行的行为,参与的主体不能否认。即发送者时候不能否认其发送消息的行为,数据接收者不能否认其接收数据的行为。
1.5 密码算法的安全性
(1)无条件安全(Unconditionally secure)
无论破译者有多少个密文,他也无法解出相应的明文。即使解出也无法验证正确性。
(2)计算上安全(Conputationally secure)
破译代价超出消息本身价值,破译时间超出信息有效期。
1.6 对加密系统的要求
(1)系统应该是实际上安全的。截获密文或已知明文对时,要决定密钥或任意明文在计算上不可行的。
(2)加密解密算法适用于密钥空间中所有元素。
(3)系统易于实现,使用方便。
(4)系统的安全性不依赖于对加密体制或加密算法的保密,而是依赖于密钥,即Kerckhoff原则。
(5)系统的使用不应使通信网络的效率过分降低。
1.7 “采用混淆、扩散和乘积的方法来设计密码”
(1)混淆
混淆:是密文和明文、密钥之间的关系复杂化。
“混淆”可以隐藏明文、密文、密钥之间的任何关系,好的“混淆”可以使复杂甚至强有力的密码分析工具不得奏效。最容易的方法是“代替”法。
(2)扩散
扩散:将每一位明文和密钥的影响扩大到尽可能多的密文位中。
“扩散”是一种将明文冗余度分散到密文中的方法。即将单个明文或密钥位的影响尽可能扩大到更多地密文中去,不仅将统计关系隐藏起来,也使密码分析者寻求明文冗余度增加了难度。最简单的“扩散”方法是“置换”法。



