[斯坦福大学2014机器学习教程笔记]第二章-梯度下降的直观理解

    在上一节中，我们给出了一个梯度下降的数学定义。在这节中，我们将更直观地感受一下这个算法是做什么的以及梯度下降算法的更新过程有什么意义。  

    这个是我们上一节所讲的梯度下降算法。让我们先简单回顾一下。

• α是什么？参数α是被称为学习速率。它控制我们以多大的幅度更新这个参数θ_j。
• 第二部分是一个导数项。

    接下来我们将主要讲这两部分分别是干什么的以及为什么要将这两部分放到一起。

    为了更好的理解，我们先举一个较为简单的例子。现在假设我们的最小化函数只有一个参数，即代价函数为J(θ1)。θ₁是一个实数，所以我们可以画出来一个曲线图。我们看一下梯度下降算法在这个函数中起什么作用。

    假设函数如下图所示。

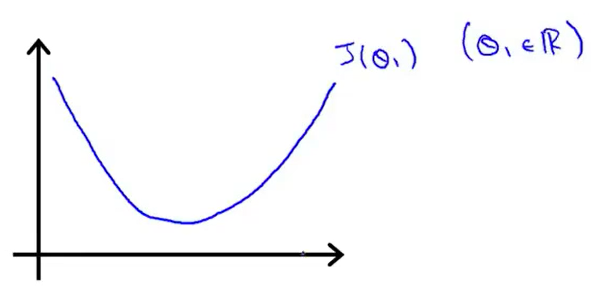    现在我们取一个点θ_1，想象一下在这个函数上从这个点出发，那么梯度下降要做的就是不断地更新θ₁（通过公式来更新）。

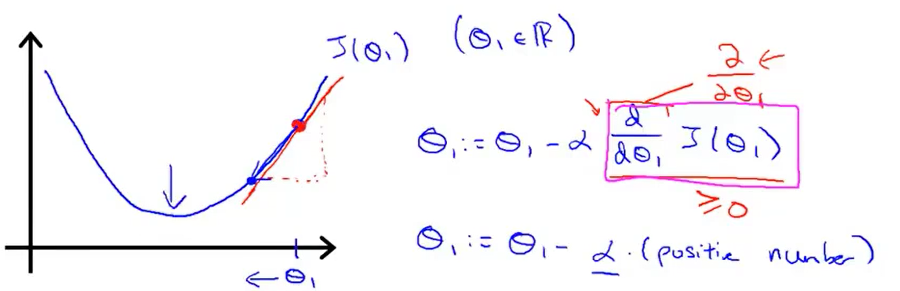
    在这个例子中，求导的目的其实就是求这个红色切线。如上图所示，显然这个切线的斜率是大于0的，那么θ₁减去一个大于0的数后(α也是大于0的)，θ₁减小，它会向左移动，显然，我们往这个方向移动是正确的。

    现在，我们取另外一个θ₁的值。此时这个倒数项对应下图的红线的斜率。我们可以看到这条直线向下倾斜，所以它的斜率小于0。那么θ₁加上一个大于0的数后(α也是大于0的)，θ₁增加，它会向右移动，显然，我们往这个方向移动是正确的。

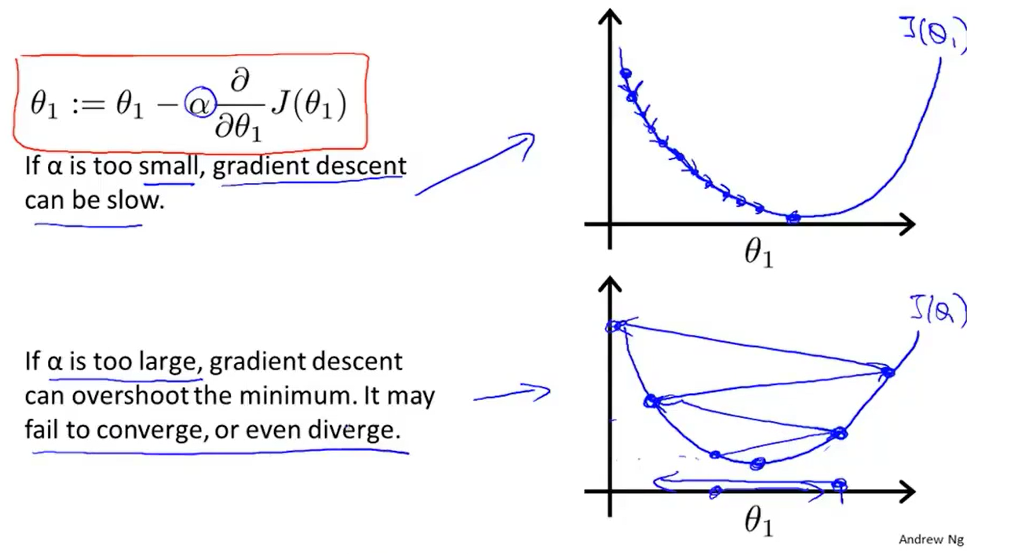
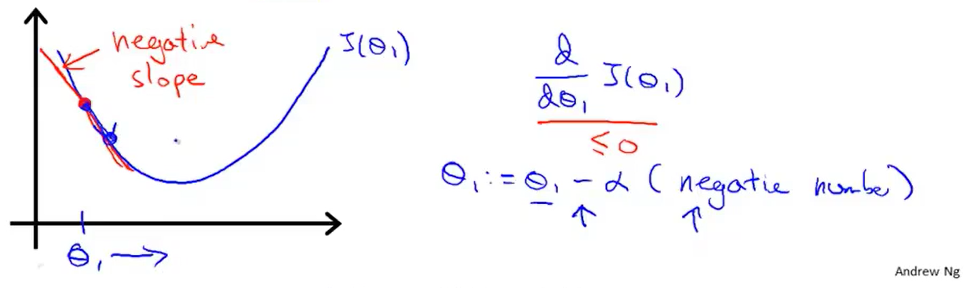    通过这个例子，我们能很直观地看到这个导数项的意义。接下来，我们将研究α究竟有什么作用。我们先来看一下如果α太大或者太小会出现什么样的情况。

（1）如果α太小时，我们更新的时候用的就是一个很小的系数。那么我们每次迈出的的步子都是非常小的。如果我们的学习速率太小，结果就是我们只能一点点地挪动。这会导致我们需要走非常多步才可以到达最低点。所以，如果α太小，那么下降的速度非常慢。

（2）那么如果α太大，那么梯度下降可能会越过最低点，甚至可能无法收敛或者发散。假设我们现在的点离最小值比较近，但因为此时α太大，那么我们会迈出很大的一步。那么此时会导致我们的代价函数变得更糟。结果，我们会发现，我们离最低点越来越远了。

    那么现在有一个问题。如果θ₁已经处在一个局部最优点，你认为下一步梯度下降会怎样？

    如图所示，此时θ₁在一个局部最优点了，我们会发现此时切线的斜率为0，那么更新之后的θ₁其实与更新之前的θ₁是一样的。相当于梯度下降法更新其实什么都没有做，他并没有改变参数值，这也正是我们想要的。因为它使我们的解始终保持在局部最优点。这也说明了即使学习速率α保持不变，梯度下降法也可以收敛到局部最低点的原因。（？如何更好理解）

    我们再来看一个例子。有一个代价函数J(θ)，我们想要求它的局部最小值。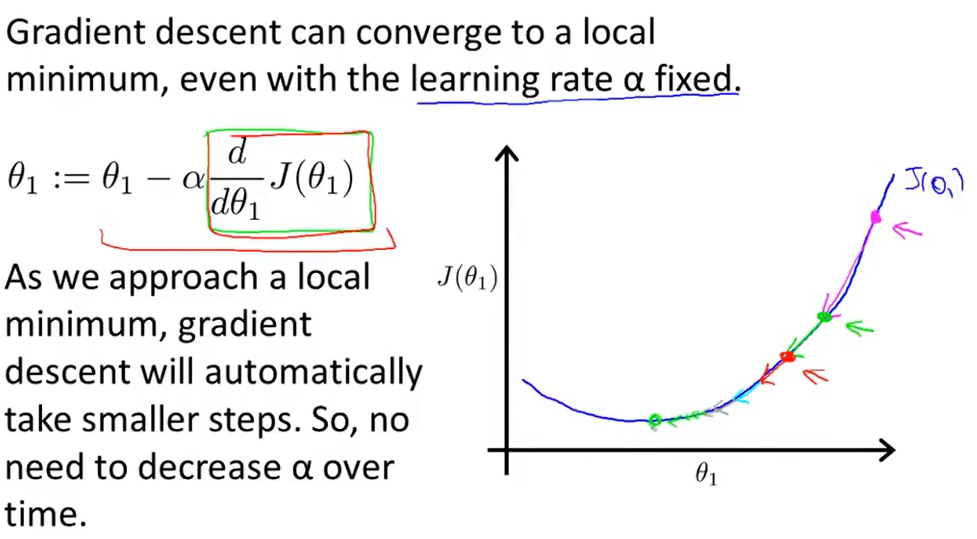     首先初始化我的梯度下降算法，在那个品红色的点初始化，如果我更新一步梯度下降，也许它会带我到这个点，因为这个点的导数是相当陡的。

    现在，我们在这个绿色的点，如果我再更新一步，你会发现我的导数，也即斜率，是没那么陡的。随着我接近最低点，我的导数越来越接近零，所以，梯度下降一步后，新的导数会变小一点点。然后我想再梯度下降一步，在这个绿点，我自然会用一个稍微跟刚才在那个品红点时比再小一点的一步，到了新的红色点，更接近全局最低点了，因此这点的导数会比在绿点时更小。所以，我再进行一步梯度下降时，我的导数项是更小的，𝜃₁更新的幅度就会更小。所以随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值。    

    回顾一下，在梯度下降法中，根据定义在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小α。