[斯坦福大学2014机器学习教程笔记]第二章-代价函数(2)
这一节,我们将更直观得理解代价函数的作用。
首先,我们复习一下之前讲的内容。
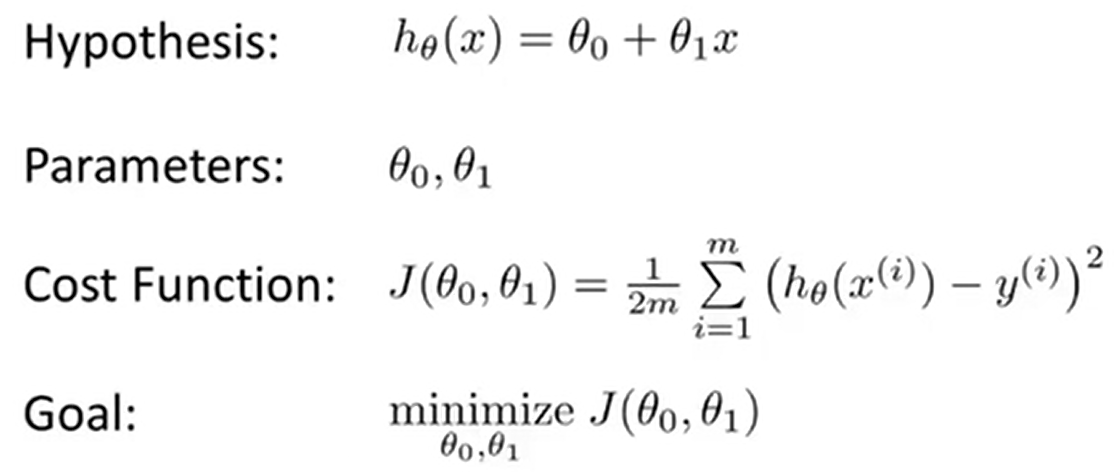 和上一节不同,这节讨论的时候保留全部参数,即θ0和θ1。
和上一节不同,这节讨论的时候保留全部参数,即θ0和θ1。
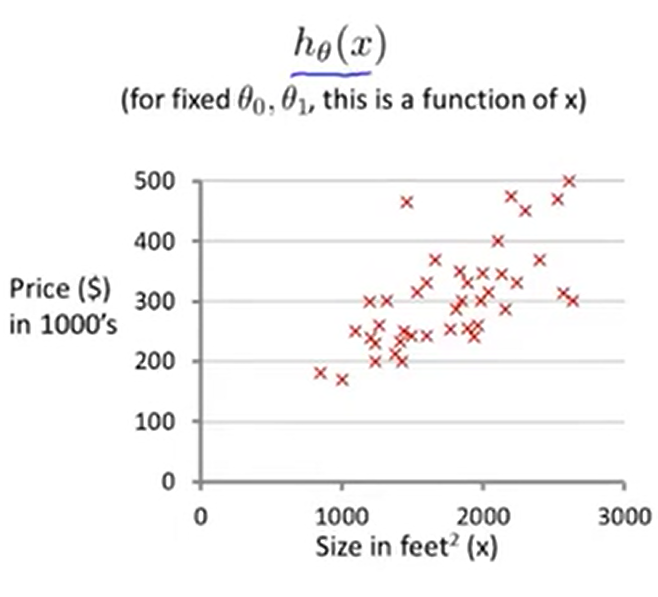
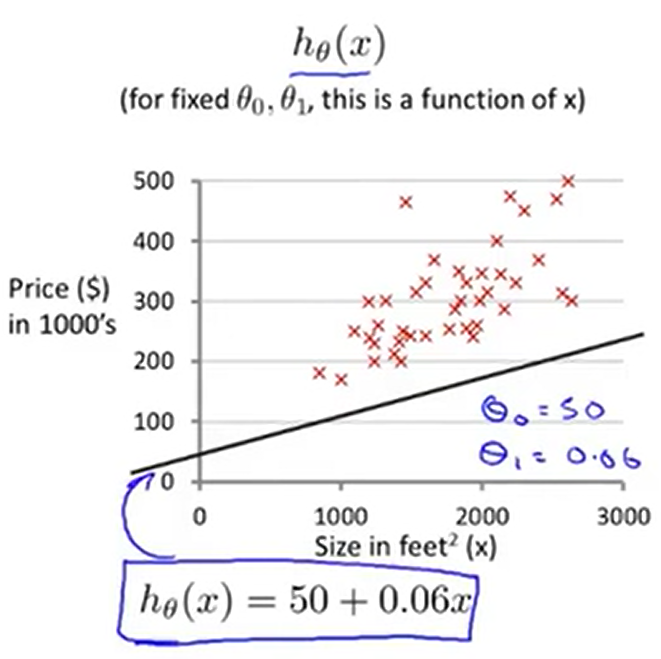
现在我们有一个关于住房价格的训练集,让我们来做一些假设,假设hθ(x)=50+0.06x,画出直线如下图,显然这是一个不太好的假设,我们此时能算出J(50,0.06)的值。
在上一讲中,我们得到的图形为一个曲线,在这节中我们得到的是一个3D曲面图。(纵轴坐标为θ0和θ1)
 当你改变θ0和θ1这两个参数的时候,你会得到不同的代价函数J(θ0,θ1)的值。点J(θ0,θ1)对应的曲面的高度就是J(θ0,θ1)的值。下面我们不会用3D曲面图来表示,我们会有等高线图来表示。下面是一些等高线图的例子。
当你改变θ0和θ1这两个参数的时候,你会得到不同的代价函数J(θ0,θ1)的值。点J(θ0,θ1)对应的曲面的高度就是J(θ0,θ1)的值。下面我们不会用3D曲面图来表示,我们会有等高线图来表示。下面是一些等高线图的例子。
 右侧的图中,轴分别为θ0和θ1,其中每一个椭圆形代表着一系列J(θ0,θ1)值相等的点。右图上取一个点(图上的红点,大概是θ0=800,θ1=-0.15),所对应的函数如左图所示,显然这并没有很好地拟合训练集。我们观察右图就会发现,它的值其实离最小值还是非常远的,可见这是一个相当高的代价(拟合得非常不好)。
右侧的图中,轴分别为θ0和θ1,其中每一个椭圆形代表着一系列J(θ0,θ1)值相等的点。右图上取一个点(图上的红点,大概是θ0=800,θ1=-0.15),所对应的函数如左图所示,显然这并没有很好地拟合训练集。我们观察右图就会发现,它的值其实离最小值还是非常远的,可见这是一个相当高的代价(拟合得非常不好)。
我们再来看另外几个例子。我们发现离最小值越近的时候拟合得越好。

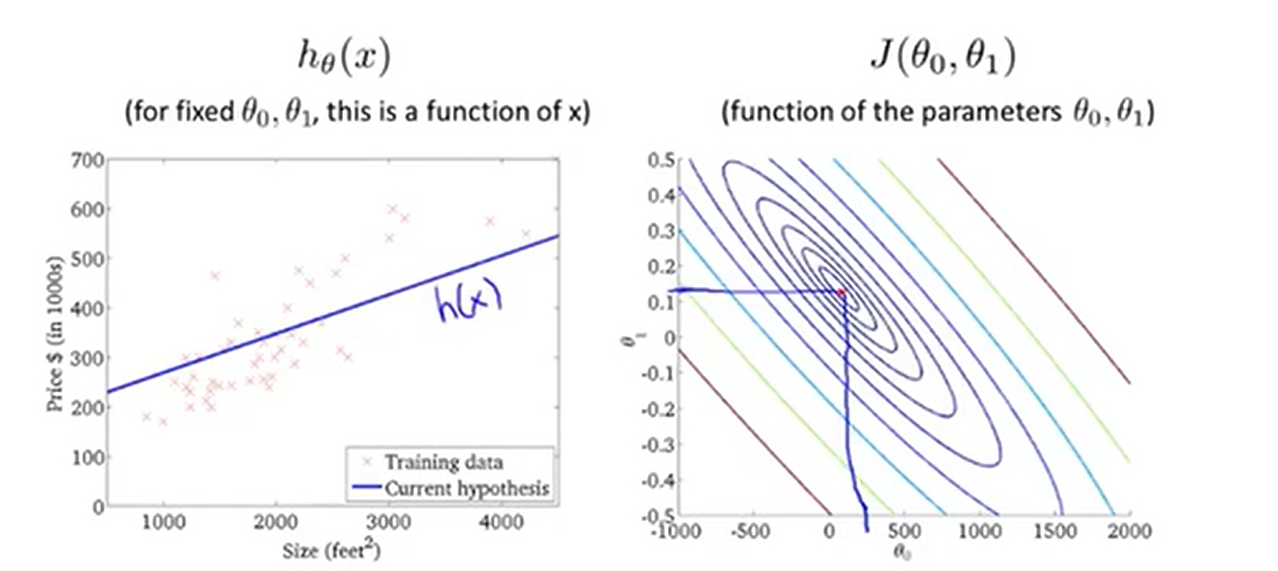
越接近最小值的假设,对应着越好的假设函数。
去更远的地方 见更亮的光



