利用SPSS做多元线性回归

这里做的是RH（土壤相对湿度）和PA、SPI、MI、MCI之间的关系：

 

 

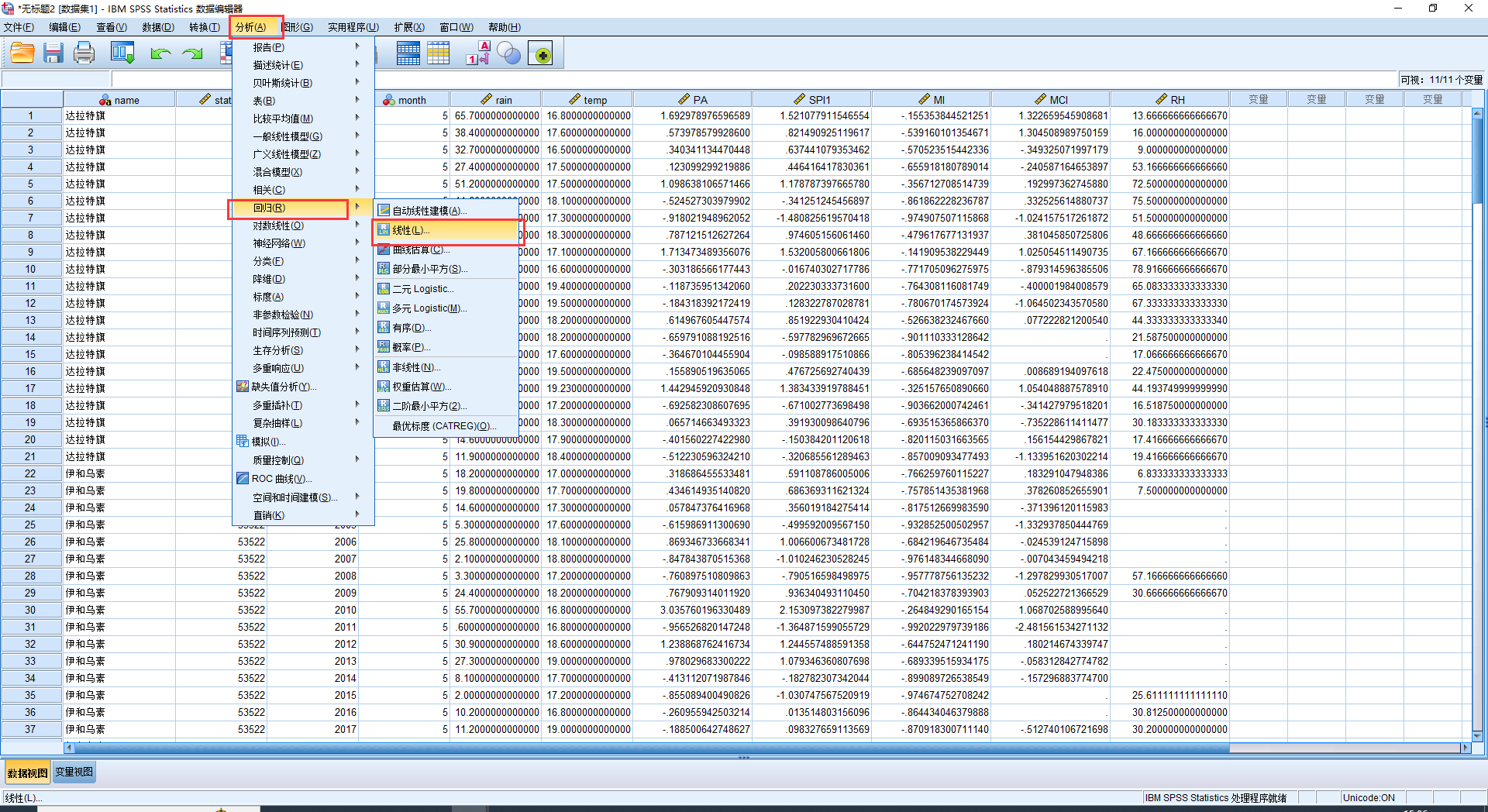
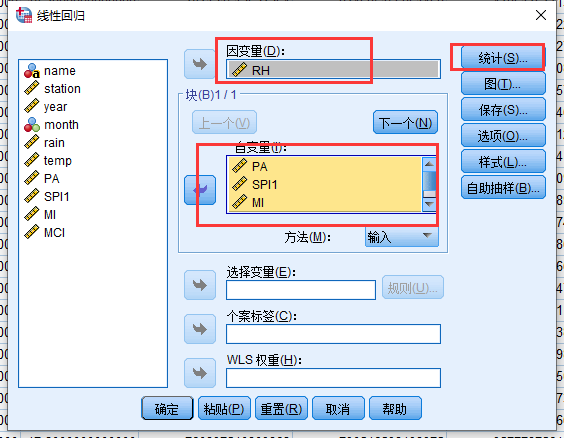
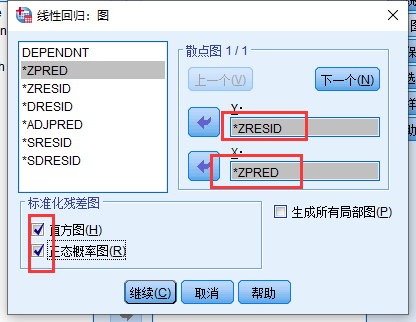
 结果：

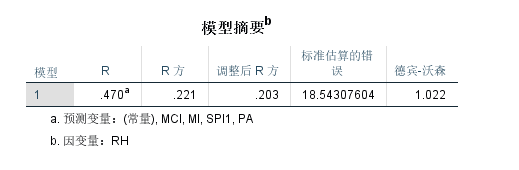
 看下R方，0.221，说明预测变量PA、SPI、MI、MCI能够解释因变量RH 22.1%，证明RH的波动只有22.1%是由于PA、SPI、MI、MCI造成的，一般统计学要求30%以上是可以接受的。实际数据达到10%就算好的了，一般10%可以接受。

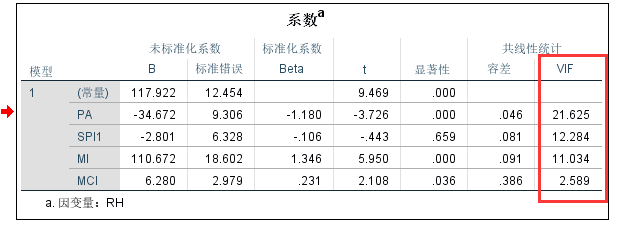
 具体分析PA、SPI、MI、MCI能不能影响RH，PA对应的显著性0.000，小于0.05意味着PA显著影响RH，影响系数B为-34.672 ，PA显著负向影响RH ，即RH越大，PA越小，SPI1显著性为0.659，大于0.05意味着，不显著。

可以得到回归方程：RH=117.922-34.672PA-2.801SPI1+110.672MI+6.280MCI

回归方程诊断：

回归分析第一个前提条件的假设为要求变量之间是相互独立的，要保证回归方程的结果（系数a那个表）是稳定可靠的，第一件事情是要核对这些自变量是否相互独立

得看这个德宾-沃森统计量。

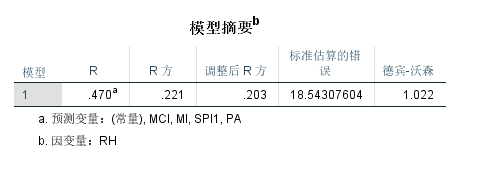
 德宾-沃森在2.0左右，被认为样本独立，我为1.022，样本独立性存疑。

第二个诊断为变量之间不存在多重共线性，参与研究的变量之间如果存在极强的关系意味着两个变量代表着同一个东西，有极强的共线性导致回归的结果作废。VIF小于5

就意味着变量之间不存在多重共线性，医学里放宽到10，经济学里放宽到30.我这里PA、SPI1、MI大于5证明这3个数之间存在多重共线性，得去几个指标。

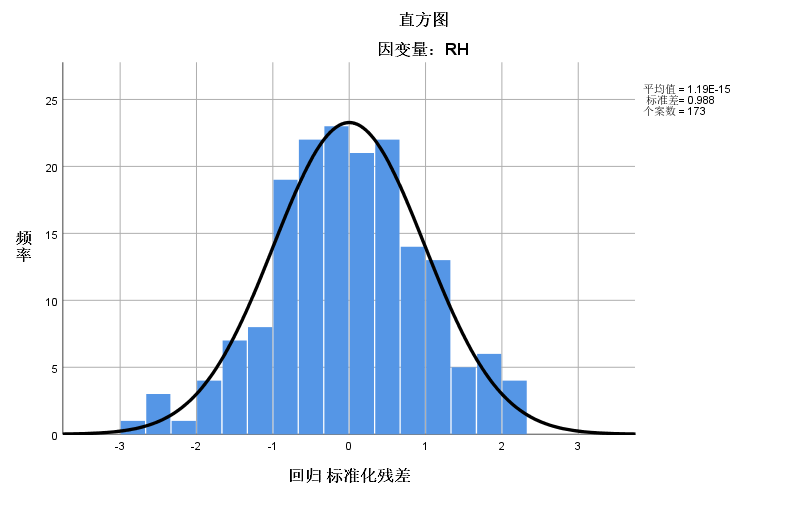
 第三个诊断为残差的正态性问题，看起来残差基本服从正态分布。