[学习笔记] 树链剖分

树链剖分的用处

使用树剖将整棵树剖分为若干条链，组成线性结构，可以方便用其他的数据结构维护信息。

一些定义

重儿子：该节点的所有子节点中子树大小最大的点。

轻儿子：该节点的所有除重儿子外的子节点。

重边：连接重儿子与父节点的边。

轻边：除重边外的边。

重链：由一串重边组成的链。

轻链：由一串轻边组成的链。

一些性质

• 树上的每个节点都属于且仅属于一条重链。
• 树链剖分后，一棵子树中的所有节点是连续的。
• 树链剖分后，一条链上的所有节点是连续的。
• 所有轻儿子的子树大小不超过父节点树大小的一半。
• 从根到某点的路径上，不超过 \(O(log_N)\) 条重链。

实现方法

P3384 【模板】重链剖分/树链剖分 - 洛谷

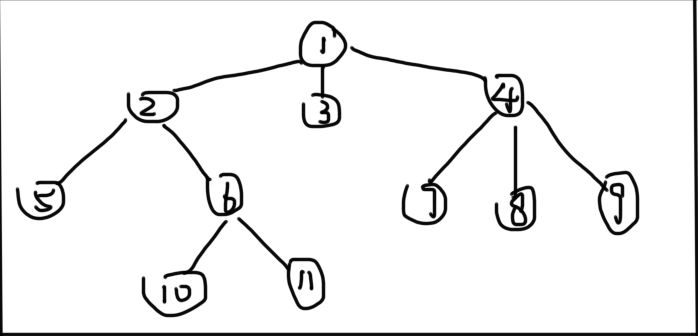
现在有一棵树：

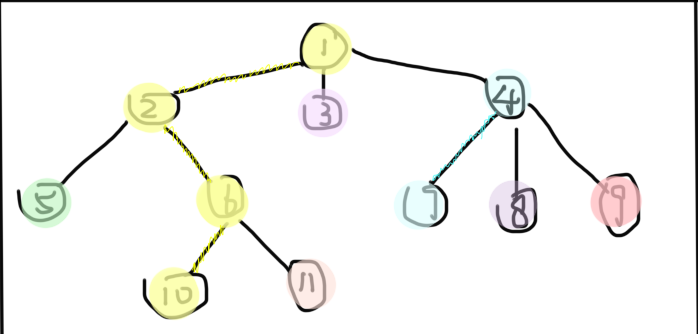
1、一个dfs记录每个点的父亲、子树大小、重儿子编号

图中同一种颜色的点属于一条链，有颜色的边为重链。

int dep[N], sz[N], son[N], p[N]; //深度 子树大小 重儿子编号 父亲 
void dfs1(int x, int fa) {
	p[x] = fa;
	dep[x] = dep[fa] + 1;
	sz[x] = 1;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == fa) continue;
		dfs1(v, x);
		sz[x] += sz[v];
		if (sz[v] > sz[son[x]]) son[x] = v;
	} 
}

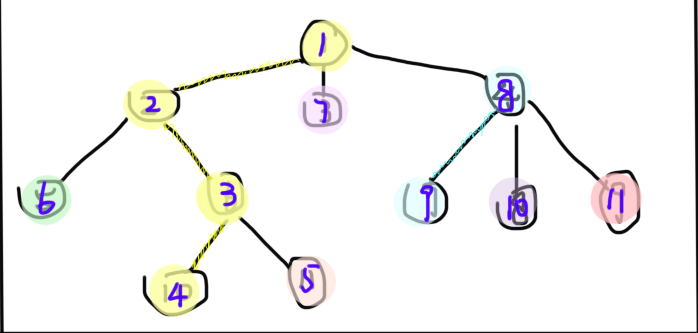
2、优先遍历重儿子，重新编号，使一条链上的点的编号连续

图中紫色数字即为重新编号后的结果。

int idx[N], top[N], idcnt; //节点新编号 节点所在重链顶端编号 
ll nnum[N];
void dfs2(int x, int rt) {
	idx[x] = ++idcnt;
	nnum[idx[x]] = num[x];
	top[x] = rt;
	if (!son[x]) return ;
	dfs2(son[x], rt);
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == p[x] || v == son[x]) continue;
		dfs2(v, v);
	}
}

3、建一棵线段树用于维护链的信息

本题需要实现一棵求区间和的线段树。

完整代码

const int N = 100010;
int n, m, s;
ll mod; //节点个数 操作个数 根节点编号 模数 
ll num[N]; //节点初值
int last[N], cnt;
struct edge {
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
} 
int dep[N], sz[N], son[N], p[N]; //深度 子树大小 重儿子编号 父亲 
void dfs1(int x, int fa) {
	p[x] = fa;
	dep[x] = dep[fa] + 1;
	sz[x] = 1;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == fa) continue;
		dfs1(v, x);
		sz[x] += sz[v];
		if (sz[v] > sz[son[x]]) son[x] = v;
	} 
}
int idx[N], top[N], idcnt; //节点新编号 节点所在重链顶端编号 
ll nnum[N];
void dfs2(int x, int rt) {
	idx[x] = ++idcnt;
	nnum[idx[x]] = num[x];
	top[x] = rt;
	if (!son[x]) return ;
	dfs2(son[x], rt);
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == p[x] || v == son[x]) continue;
		dfs2(v, v);
	}
}
struct SegmentTree {
	ll l[N << 2], r[N << 2], sum[N << 2], add[N << 2];
	void build(int rt, int L, int R) {
		l[rt] = L, r[rt] = R;
		if (L == R) {sum[rt] = nnum[L]; return ;}
		int mid = L + R >> 1;
		build(rt << 1, L, mid), build(rt << 1 | 1, mid + 1, R);
		update(rt);
	}
	void update(int rt) {
		sum[rt] = (sum[rt << 1] + sum[rt << 1 | 1]) % mod;
	}
	void pushdown(int rt) {
		add[rt << 1] = (add[rt << 1] + add[rt]) % mod, add[rt << 1 | 1] = (add[rt << 1 | 1] + add[rt]) % mod;
		sum[rt << 1] = (sum[rt << 1] + (r[rt << 1] - l[rt << 1] + 1) * add[rt] % mod) % mod;
		sum[rt << 1 | 1] = (sum[rt << 1 | 1] + (r[rt << 1 | 1] - l[rt << 1 | 1] + 1) * add[rt] % mod) % mod;
		add[rt] = 0;
	}
	void change(int rt, int L, int R, ll c) {
		if (R < l[rt] || r[rt] < L) return ;
		if (L <= l[rt] && r[rt] <= R) {
			add[rt] = (add[rt] + c) % mod;
			sum[rt] = (sum[rt] + (r[rt] - l[rt] + 1) * c % mod) % mod;
			return ;
		}
		pushdown(rt);
		if (L <= r[rt << 1]) change(rt << 1, L, R, c);
		if (l[rt << 1 | 1] <= R) change(rt << 1 | 1, L, R, c);
		update(rt);
	}
	ll query(int rt, int L, int R) {
		if (R < l[rt] || r[rt] < L) return 0;
		if (L <= l[rt] && r[rt] <= R) return sum[rt];
		pushdown(rt);
		ll res = 0;
		if (L <= r[rt << 1]) res = (res + query(rt << 1, L, R)) % mod;
		if (l[rt << 1 | 1] <= R) res = (res + query(rt << 1 | 1, L, R)) % mod;
		update(rt);
		return res;
	}
} tree;
void treeadd(int x, int y, ll c) {
	while(top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]]) swap(x, y);
		tree.change(1, idx[top[x]], idx[x], c);
		x = p[top[x]];
	}
	if (dep[x] > dep[y]) swap(x, y);
	tree.change(1, idx[x], idx[y], c);
}
ll treequery(int x, int y) {
	ll res = 0;
	while (top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]]) swap(x, y);
		res = (res + tree.query(1, idx[top[x]], idx[x])) % mod;
		x = p[top[x]]; 
	}
	if (dep[x] > dep[y]) swap(x, y);
	res = (res + tree.query(1, idx[x], idx[y])) % mod;
	return res;
}
int main() {
	n = read(), m = read(), s = read(), mod = read();
	for (int i = 1; i <= n; i++) num[i] = read() % mod;
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		addedge(x, y), addedge(y, x); 
	}
	dep[s] = 1;
	dfs1(s, s),	dfs2(s, s);
	tree.build(1, 1, n); 
	for (int i = 1; i <= m; i++) {
		int op = read();
		if (op == 1) {
			int x = read(), y = read(), c = read() % mod;
			treeadd(x, y, c);
		}
		if (op == 2) {
			int x = read(), y = read();
			printf("%lld\n", treequery(x, y));
		}
		if (op == 3) {
			int x = read(), c = read() % mod;
			tree.change(1, idx[x], idx[x] + sz[x] - 1, c); 
		}
		if (op == 4) {
			int x = read();
			printf("%lld\n", tree.query(1, idx[x], idx[x] + sz[x] - 1));
		}
	}
	return 0;
}