[题解] [CSP-J 2022] 逻辑表达式 思路整理
标签:分治。
题目传送门:P8815 [CSP-J 2022] 逻辑表达式
题目大意
给一个包含 0 、1、|、&、(、) 的逻辑表达式(保证正确)。
在计算表达式时采用“短路”策略:
- 计算表达式
a&b时,先计算a,如果表达式a的值为b,记为一处& 短路。 - 计算表达式
a|b时,先计算a,如果表达式a的值为b,记为一处| 短路。
现需计算表达式的值,并输出计算过程中 & 短路 和 | 短路 的出现次数。
注:在一个逻辑表达式中还可能有括号。规定在运算时,括号内的部分先运算;两种运算并列时,& 运算优先于 | 运算;同种运算并列时,从左向右运算。
思路
首先观察样例。 考虑计算过程。
首先你观察到了中间的 |,并从这里把表达式分成了两段。
你先考虑左边那一段。你观察到了中间的 &,并从这里把左半部分表达式分成了两段。
你发现左半部分表达式的左半部分值为 & 短路。
于是表达式变成了这样:
现在你把左半部分处理完了,你将目光投向右半部分。
你观察到了一个 |,并从这里把右半部分表达式分成了两段。
你开始处理左半部分的右半部分。你观察到了一个 |,并从这里把表达式分成了两段。
你发现左半部分表达式的左半部分值为 | 短路。
于是表达式变成了这样:
然后你注意到先前观察到的 | 左半部分值为 | 短路。
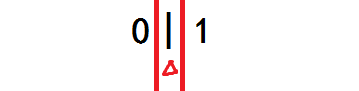
于是表达式变成了这样:
智慧的你一眼看出表达式的值为
综上,表达式的值为 | 短路,& 短路。
这是人工处理表达式时的计算过程,那么又该如何让程序实现这个过程呢?
注意到每次处理时,首先找到了当前层(一对括号记为一层)最靠右的 |,并从该位置分成左右两段分别进行操作。因此是对原表达式进行分治。
当没有 | 时,去寻找最靠右的 &,进行类似的分段处理。
但如果直接进行分治,每次遍历一遍字符串去找最右边的 | 或者 &,会 TLE 到飞起。
考虑进行一个预处理。对于每个位置,处理出与它同层的字符中,离它最近的 | 或者 & 在哪里。
不难写出以下程序:
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (c[i] == '(') cnt++;
if (c[i] == ')') lastor[cnt] = lastand[cnt] = 0, cnt--;
if (c[i] == '|') lastor[cnt] = i;
if (c[i] == '&') lastand[cnt] = i;
sand[i] = lastand[cnt], sor[i] = lastor[cnt];
}
其中 | 的位置,& 的位置。
| 的位置,& 的位置。
注意:这个“同层”指的是在同一对括号内,所以要记得清空 不过好像不清空也是对的(因为具体实现时会判掉不在同一括号内的情况)
那么也不难写出分治的函数了:
int solve(int l, int r) {
if (sor[r] >= l) { // 区间内有 '|'
int res = solve(l, sor[r] - 1);
if (res == 1) {
cntor++;
return 1;
}
return (res | solve(sor[r] + 1, r));
}
if (sand[r] >= l) { // 区间内有 '&'
int res = solve(l, sand[r] - 1);
if (res == 0) {
cntand++;
return 0;
}
return (res & solve(sand[r] + 1, r));
}
if (c[l] == '(' && c[r] == ')') return solve(l + 1, r - 1); // 匹配到一对括号, 将其去掉
return c[l] ^ 48; // 以上情况都不是, 那么只能是数字
}
注意:拆括号不能放在函数的最开头。
为什么?因为我错过,请观察一下样例二,如果在开头去括号,当你由最右边的 & 把表达式分成两段后,你会将第
完整代码
const int N = 1000010;
char c[N];
int n, sand[N], sor[N], lastand[N], lastor[N];
int cntand, cntor;
int solve(int l, int r) {
if (sor[r] >= l) {
int res = solve(l, sor[r] - 1);
if (res == 1) {
cntor++;
return 1;
}
return (res | solve(sor[r] + 1, r));
}
if (sand[r] >= l) {
int res = solve(l, sand[r] - 1);
if (res == 0) {
cntand++;
return 0;
}
return (res & solve(sand[r] + 1, r));
}
if (c[l] == '(' && c[r] == ')') return solve(l + 1, r - 1);
return c[l] ^ 48;
}
int main() {
scanf("%s", c + 1);
n = strlen(c + 1);
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (c[i] == '(') cnt++;
if (c[i] == ')') lastor[cnt] = lastand[cnt] = 0, cnt--;
if (c[i] == '|') lastor[cnt] = i;
if (c[i] == '&') lastand[cnt] = i;
sand[i] = lastand[cnt], sor[i] = lastor[cnt];
}
int ans = solve(1, n);
printf("%d\n%d %d\n", ans, cntand, cntor);
return 0;
}
完结撒花~
本文作者:shiranui
本文链接:https://www.cnblogs.com/shiranui/p/16879563.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。



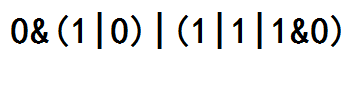
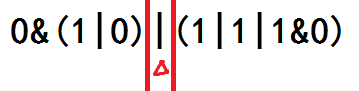
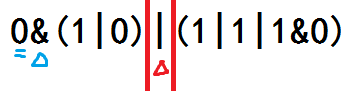
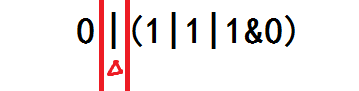
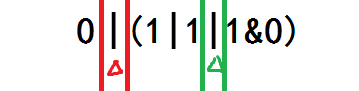
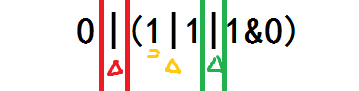
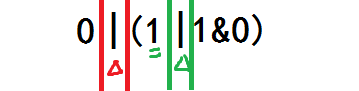



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步