[学习笔记] 最近公共祖先（LCA）
研究了LCA，写篇笔记记录一下。
讲解使用例题 P3379 【模板】最近公共祖先（LCA）。
什么是LCA
最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。
—— 摘自 OI Wiki
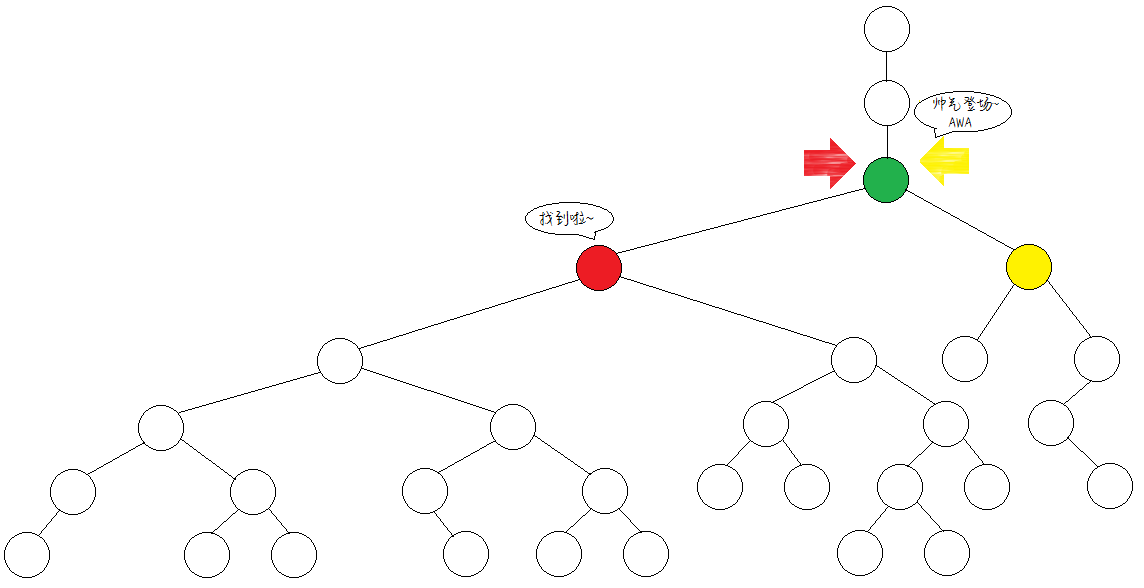
比如下图红、黄两点的LCA就是绿点。
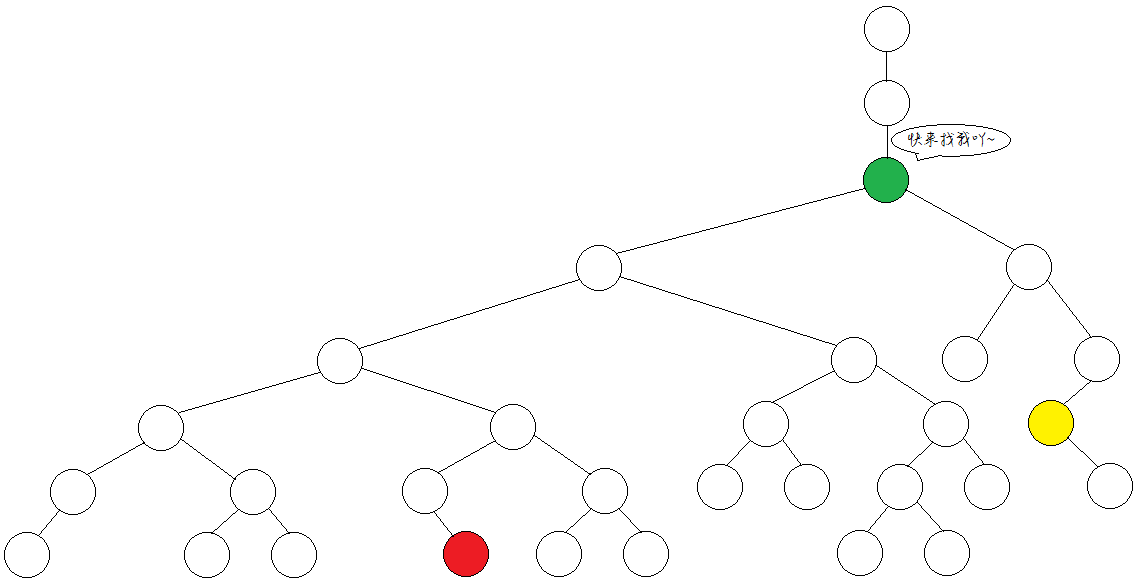
LCA的几种实现方式
向上标记法
从 x 点一直向上走直到到达根节点，在走的过程中标记所有经过的点。
从 y 点一直向根节点走，遇到的第一个标记过的点即为两点的LCA。
代码略
树上倍增法
新数据前两个点被卡TLE了/kk
首先，我们将要求、lca的两点跳到同一深度，如下图：
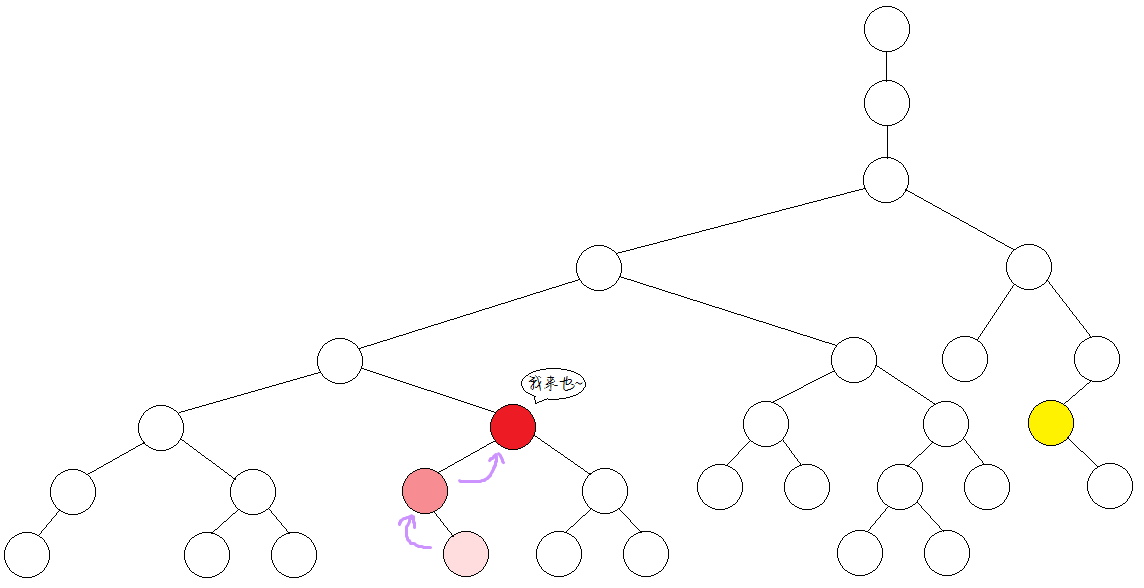
然后两点同时向上从大到小倍增，直到到的两点不相同，继续往上跳。
先尝试向能跳的最远处跳（4步）。
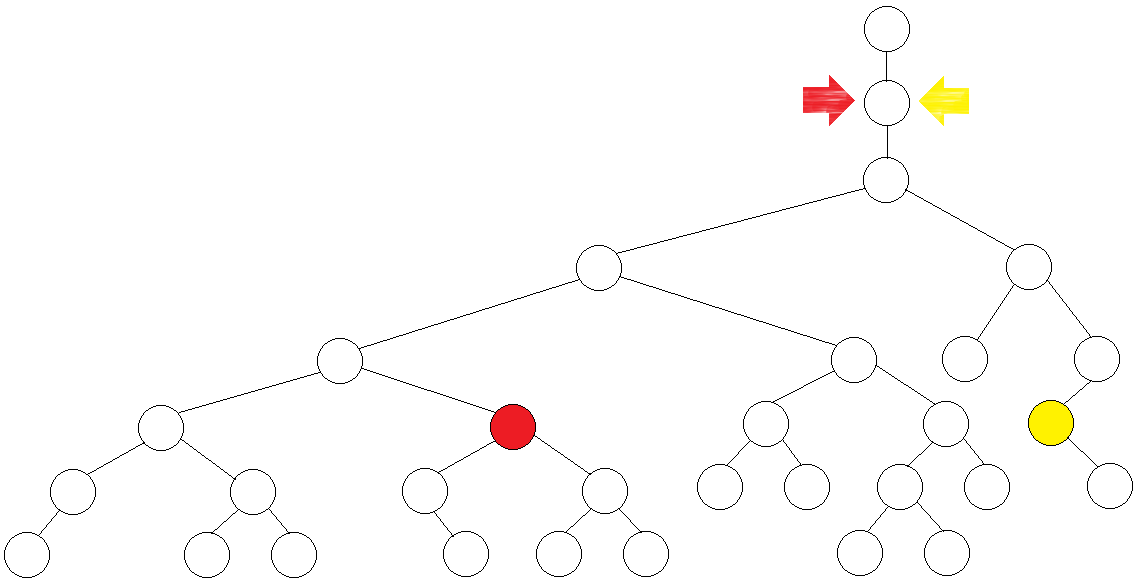
我们发现两个点在同处汇合，不行，考虑少跳一半（2步）。
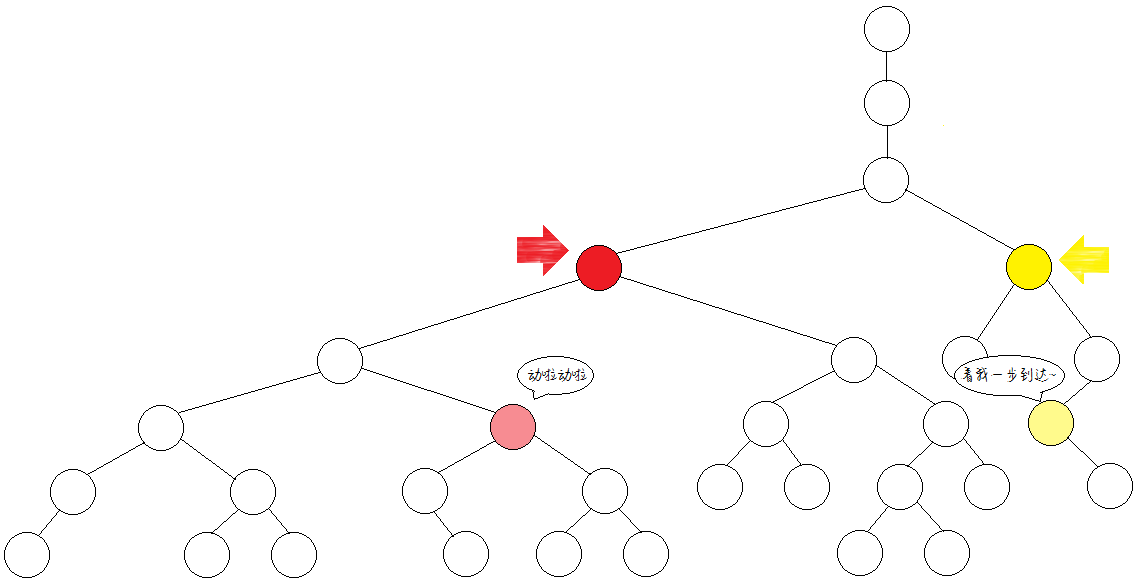
不同点，跳上。继续少跳一半（1步）。
同一个点，不跳。
此时，所有的跳跃尝试结束。由于目前两点不在同处，故再往上跳一步。
于是就找到这两个点的LCA啦！
（是不是讲的云里雾里的，结合代码理解一下吧~）
代码实现
- dfs获取每个点的深度
int p[N], dep[N];
void dfs(int x, int f) {
p[x] = f;
for (int i = last[x]; i; i = e[i].next) { //我用邻接表存的图
int v = e[i].to;
if (v == f) continue;
dep[v] = dep[x] + 1;
dfs(v, x);
}
}
dep[s] = 1;
dfs(s, s); //将起点的父节点设为自己，这样跳多了也不会出锅
- 预处理倍增跳到的点
for (int i = 1; i <= n; i++) f[0][i] = p[i];
for (int j = 1; j <= lg; j++) // 跳 2^j 步 lg 为 log2(n)
for (int i = 1; i <= n; i++) // 第 i 个点
f[j][i] = f[j - 1][f[j - 1][i]];
// 跳 2^j 步到的点即为先跳 2^(j-1) 步再跳 2^(j-1) 步到的点
- 处理LCA
（没有写成函数QAQ）
int a = read(), b = read();
if (dep[a] > dep[b]) swap(a, b); //使 a 的深度小于等于 b
for (int i = lg; i >= 0; i--)
if (dep[f[i][b]] >= dep[a]) b = f[i][b]; //将 a 与 b 跳到同一深度
for (int i = lg; i >= 0; i--) //从最远的距离开始尝试 （跳 2^i 步）
if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a]; //不是同一个点就跳上去
if (a != b) a = p[a];
//结束后不是同一个点，那么LCA就是目前这个点的父节点，所以也可以写成 b = p[b] 然后输出 b
printf("%d\n", a);
- 为什么尝试跳只用从 log2(n) 循环一遍到 0 就行？
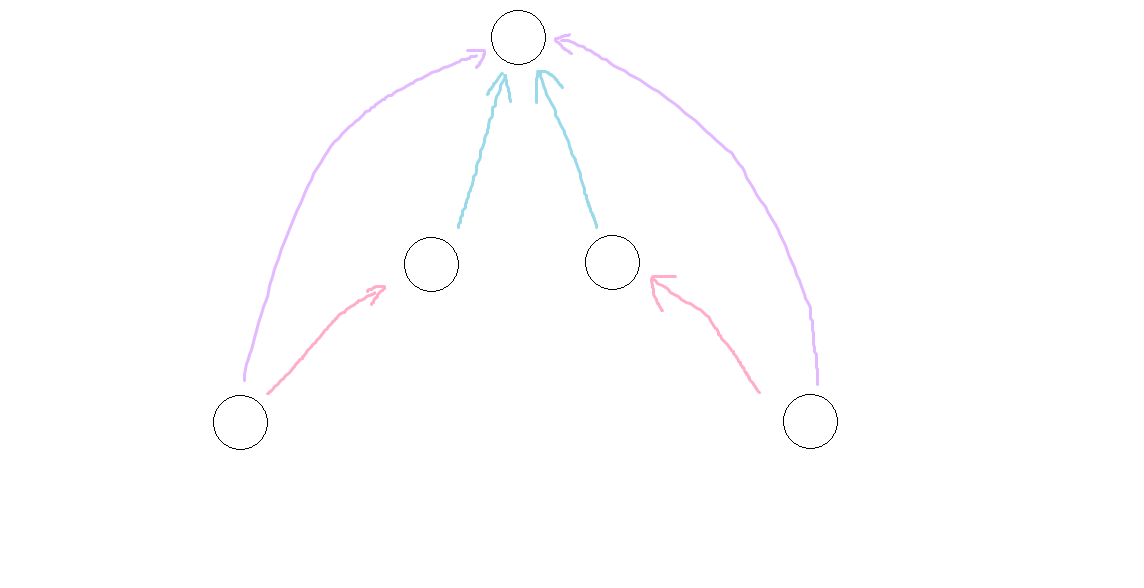
按照代码思路，我们会先尝试沿紫色路径跳 2^j 步，由于不成功，我们折半跳 2^(j-1) 步，沿粉边跳上。
此时若在沿蓝边跳 2^(j-1) 步，又跳到了原来粉边指向的点，我们已经知道那个点不行，所以不用尝试跳上，而应该继续尝试跳 2^(j-2) 步。
完整代码（点击查看）
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge {
int to, next;
} e[N << 1];
void addedge(int x, int y) {
e[++cnt].to = y;
e[cnt].next = last[x];
last[x] = cnt;
}
int p[N], dep[N];
void dfs(int x, int f) {
p[x] = f;
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == f) continue;
dep[v] = dep[x] + 1;
dfs(v, x);
}
}
int f[19][N], lg;
int main() {
n = read(), m = read(), s = read();
lg = log2(n);
for (int i = 1; i < n; i++) {
int u = read(), v = read();
addedge(u, v), addedge(v, u);
}
dep[s] = 1;
dfs(s, s);
for (int i = 1; i <= n; i++) f[0][i] = p[i];
for (int j = 1; j <= lg; j++)
for (int i = 1; i <= n; i++)
f[j][i] = f[j - 1][f[j - 1][i]];
while (m--) {
int a = read(), b = read();
if (dep[a] > dep[b]) swap(a, b);
for (int i = lg; i >= 0; i--)
if (dep[f[i][b]] >= dep[a]) b = f[i][b];
for (int i = lg; i >= 0; i--)
if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a];
if (a != b) a = p[a];
printf("%d\n", a);
}
return 0;
}
LCA的Tarjan算法
本质来说，其实就是用并查集对“向上标记法”进行优化。
注意：操作是离线的。
从根节点开始进行 DFS，对于每个搜到的点打上标记，在回溯时将该结点并入其父节点的集合，具体操作见下。
- 如何离线？
我们先把 m 次询问都读入，然后再相关的两个结点上分别挂上询问。
- 为什么要两点都挂上询问
因为我们并不知道两个点谁先访问谁后访问，不好处理。
比如现在给一棵树，询问红、黄两点的 LCA 。
我们对这棵树进行 DFS，目前已经搜到了黄点，上方的三个不同深度的橙点表示 DFS 过程中栈里的点。
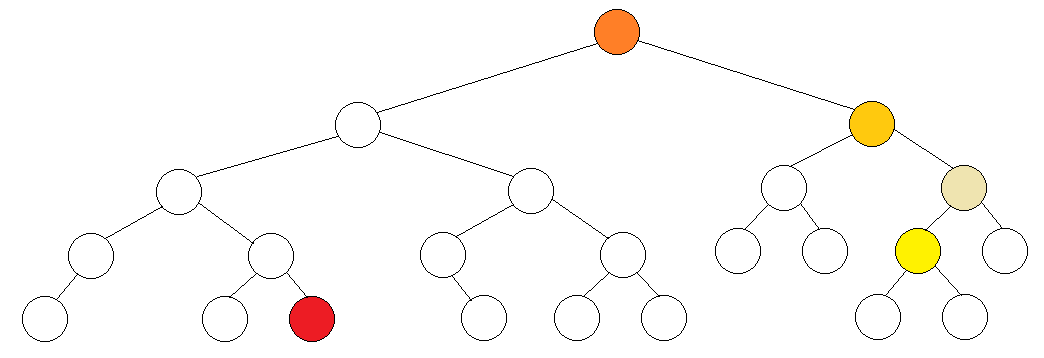
由于已经搜过了根节点的左子树，所以红点已打过标记。根节点的左子树与根节点属于一个集合，第二层的黄点的左子树与它自己属于一个集合。
现在在黄点上打个标记，发现黄点上挂的关于红点的询问可以处理了（两点都已搜到）。
红、黄两点的LCA即为红点所在集合的根节点，即图中树的根节点。
（讲的有亿点点乱诶）
代码实现
- 存储询问
struct node { //为了保证输出顺序，不仅要把询问挂在点上，还要额外存一下
int x, y, ans;
} ask[N];
vector <int> g[N]; //每个点上挂的询问
for (int i = 1; i <= m; i++) {
ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
g[ask[i].x].push_back(i);
g[ask[i].y].push_back(i);
}
- DFS
int p[N];
bool vis[N]; //访问标记
int r[N]; //一个集合实际的根节点（并查集是按秩合并的，根节点不能保证是我们要的根节点）
void dfs(int x, int f) {
p[x] = f;
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == f) continue;
vis[v] = 1;
for (int j : g[v]) { //遍历所有询问
int o = ask[j].x;
if (o == v) o = ask[j].y;
if (!vis[o]) continue;
ask[j].ans = r[a.root(o)]; //记录询问答案
}
dfs(v, x);
a.merge(x, v); //合并两个集合
r[a.root(x)] = x; //标记实际根节点
}
}
vis[s] = 1;
dfs(s, s);
完整代码（点击查看）
const int N = 500010;
int n, m, s;
struct Disjoint_Set {
int p[N], size[N];
void build() {
for (int i = 1; i <= n; i++) p[i] = i, size[i] = 1;
}
int root(int x) {
if (p[x] != x) return p[x] = root(p[x]);
return x;
}
void merge(int x, int y) {
x = root(x), y = root(y);
if (size[x] > size[y]) swap(x, y);
p[x] = y;
size[y] += size[x];
}
bool check(int x, int y) {
x = root(x), y = root(y);
return x == y;
}
} a;
int last[N], cnt;
struct edge {
int to, next;
} e[N << 1];
void addedge(int x, int y) {
e[++cnt].to = y;
e[cnt].next = last[x];
last[x] = cnt;
}
struct node {
int x, y, ans;
} ask[N];
vector <int> g[N];
int p[N];
bool vis[N];
int r[N];
void dfs(int x, int f) {
p[x] = f;
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == f) continue;
vis[v] = 1;
for (int j : g[v]) {
int o = ask[j].x;
if (o == v) o = ask[j].y;
if (!vis[o]) continue;
ask[j].ans = r[a.root(o)];
}
dfs(v, x);
a.merge(x, v);
r[a.root(x)] = x;
}
}
int main() {
n = read(), m = read(), s = read();
a.build();
for (int i = 1; i <= n; i++) {
r[i] = i;
}
for (int i = 1; i < n; i++) {
int u = read(), v = read();
addedge(u, v), addedge(v, u);
}
for (int i = 1; i <= m; i++) {
ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
g[ask[i].x].push_back(i);
g[ask[i].y].push_back(i);
}
vis[s] = 1;
dfs(s, s);
for (int i = 1; i <= m; i++) printf("%d\n", ask[i].ans);
return 0;
}
LCA转RMQ
先贴代码吧，讲解后续再补
咕咕咕
完整代码（点击查看）
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge{
int to, next;
} e[N << 1];
void addedge(int x, int y) {
e[++cnt].to = y;
e[cnt].next = last[x];
last[x] = cnt;
}
int dep[N], a[N << 1], ed, fst[N];
void dfs(int x, int f) {
a[++ed] = x;
if (!fst[x]) fst[x] = ed;
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == f) continue;
dep[v] = dep[x] + 1;
dfs(v, x);
a[++ed] = x;
}
}
int f[21][N << 1], lg;
int main() {
n = read(), m = read(), s = read();
lg = log2(n) + 1;
for (int i = 1; i < n; i++) {
int x = read(), y = read();
addedge(x, y), addedge(y, x);
}
dep[s] = 1;
dfs(s, s);
for (int i = 1; i <= ed; i++) f[0][i] = i;
for (int j = 1; j <= lg; j++) {
for (int i = 1; i <= ed - (1 << j) + 1; i++) {
int i2 = i + (1 << (j - 1));
if (dep[a[f[j - 1][i]]] < dep[a[f[j - 1][i2]]]) f[j][i] = f[j - 1][i];
else f[j][i] = f[j - 1][i2];
}
}
for (int i = 1; i <= m; i++) {
int x = read(), y = read();
if (fst[x] > fst[y]) swap(x, y);
int len = fst[y] - fst[x] + 1, ans;
int lg2 = log2(len);
int i2 = fst[y] - (1 << lg2) + 1;
if (dep[a[f[lg2][fst[x]]]] < dep[a[f[lg2][i2]]]) ans = a[f[lg2][fst[x]]];
else ans = a[f[lg2][i2]];
printf("%d\n", ans);
}
return 0;
}
树剖
[update 2023/03/24] 研究了树剖，突然想起LCA好像也能用树剖求，所以来记录一下。
树剖部分就不多讲了，板子里有记 \(top\) 数组表示这条链最高的节点是哪个，查询的时候每次跳到这个最高点的父亲上就可以了。
完整代码（点击查看）
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge {
int to, next;
} e[N << 1];
void addedge(int x, int y) {
e[++cnt].to = y;
e[cnt].next = last[x];
last[x] = cnt;
}
int dep[N], sz[N], son[N], p[N];
void dfs1(int x, int fa) {
dep[x] = dep[fa] + 1, sz[x] = 1, p[x] = fa;
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == fa) continue;
dfs1(v, x);
sz[x] += sz[v];
if (sz[v] > sz[son[x]]) son[x] = v;
}
}
int idx[N], idcnt, top[N];
void dfs2(int x, int rt) {
idx[x] = ++idcnt, top[x] = rt;
if (!son[x]) return ;
dfs2(son[x], rt);
for (int i = last[x]; i; i = e[i].next) {
int v = e[i].to;
if (v == p[x] || v == son[x]) continue;
dfs2(v, v);
}
}
int query(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
x = p[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
int main() {
n = read(), m = read(), s = read();
for (int i = 1; i < n; i++) {
int x = read(), y = read();
addedge(x, y), addedge(y, x);
}
dep[s] = 1;
dfs1(s, s), dfs2(s, s);
for (int i = 1; i <= m; i++) {
int x = read(), y = read();
printf("%d\n", query(x, y));
}
return 0;
}
