浅谈树状数组

我们常常把树状数组和线段树相比较，一般认为树状数组的处理效率和编写复杂度优于线段树，线段树较树状数组能处理更多的信息，有人提到线段树擅长处理横向区间的问题，树状数组擅长处理纵向区间的问题，总之，在处理区间这类问题上，我们二者都要掌握。树状数组的建树复杂度为O(nlogn)，维护和查询复杂度为O(logn)。

树状数组是什么呢？我们用两张图来表示一下：

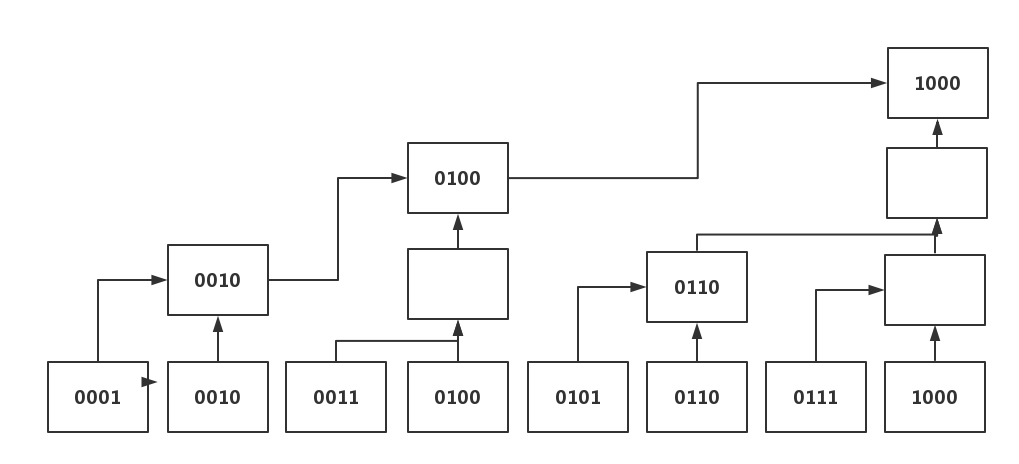
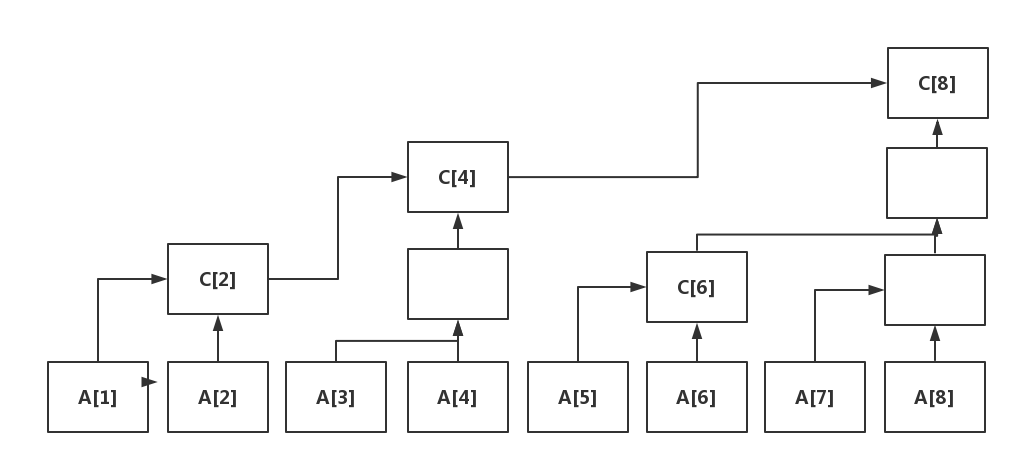
换言之，就是根据数组下标二进制1的最低位构成的一棵变形树

我们用A数组来表示原始数组，C数组来表示树状数组

0001的最低位在2^0上，C[1]只表示A[1]

0010的最低位在2^1上，C[2]表示A[1]+A[2]

0011的最低位在2^0上，C[3]表示A[3]

0100的最低位在2^2上，C[4]表示A[1]+A[2]+A[3]+A[4] = C[2]+A[3]+A[4] 

0101的最低位在2^0上，C[5]只表示A[5]

0110的最低位在2^1上，C[6]表示A[5]+A[6]

换言之，在树状数组中一个下标最低位为2的几次幂，该下标就指代它往前（包括它）往前数2的几次幂的和

如果我们要计算1到6的和

我们需要计算C[4]+C[6]

学习树状数组时，有一个必须掌握的函数：lowbit

lowbit其实就是取出x的二进制的最低位1，比如0110这个二进制数，lowbit(6) = 2

具体实现如下

int lowbit(int n)
{
    return n & -n;
}

计算机中负数使用对应的正数的补码来表示
例如 : n=6（0110）
-n=-6=(1001+1)=(1010)
n&(-n)=(0010)=2=2^1

即最低位1在2^1的位置上

 

所以我们计算1到6的和时

就可以先算SUM += C[6]

再6 - lowbit(6) = 4

再算SUM += C[4]

4 - lowbit(14) = 0 结束运算

int search(int n)
{
    int sum = 0;
    while (n)
    {
        sum += c[n];
        n -= lowbit(n);
    }
    return sum;
}

 

在更新时方向则相反，我们假设原始数据是一个长度为6的数组

我需要更新下标为1的数据是，更新顺序为：

先更新C[1],1+lowbit(1) = 2

再更新C[2],2+lowbit(2) = 4

4+lowbit(4) = 8 > 6

更新停止

 

更新和初始化树状数组函数如下：

void update(int n, int pos, int val)
{
    while (pos <= n)
    {
        c[pos] += val;
        pos += lowbit(pos);
    }
}

void init(int n)
{
    memset(c, 0, sizeof(c));
    for (int i = 1; i <= n; i++)
        update(n, i, a[i]);
}

 

在学习树状数组时，一定时刻注意要用二进制的思想来去思考，而这一算法的优势之处也是在此

这里再附上求1到x和的模板：

#include <iostream>
#include <string.h>

using namespace std;

int a[1050];//原始数据
int c[1050];//树状数组

int lowbit(int n)
{
    return n & -n;
}

void update(int n, int pos, int val)
{
    while (pos <= n)
    {
        c[pos] += val;
        pos += lowbit(pos);
    }
}

void init(int n)
{
    memset(c, 0, sizeof(c));
    for (int i = 1; i <= n; i++)
        update(n, i, a[i]);
}

int search(int n)
{
    int sum = 0;
    while (n)
    {
        sum += c[n];
        n -= lowbit(n);
    }
    return sum;
}

int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    while (cin >> n >> m)
    {
        for (int i = 1; i <= n; i++)
            cin >> a[i];

        init(n);

        while (m--)
        {
            int t;
            cin >> t;
            cout << search(t) << endl;;
        }
    }

    return 0;
}

如果还是有些懵的话，这里再推荐一个更详细的入门讲解：https://www.cnblogs.com/acgoto/p/8583952.html#4046752

后面我们再详谈求区间最值和逆序对的方法