NumPy数组图解

N维数组的属性

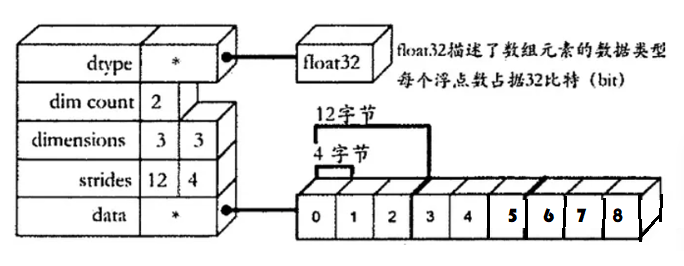
　　如果说强大而完备的第三方库，赋予了Python独特的魅力，那么N维数组(ndarray)便使得 NumPy拥有了灵魂。我们仅以NumPy的一维数组为例介绍了一些函数的应用。 而实际上，在机器学习中，要处理的数组大多数是N维的。 需要说明的是，在物理内存中是不存在N维数组的，限于存储介质的物理特性，它永远只有一维结构。

可视化物理内存分布：

 

NumPy数组的逻辑图（数学）

 

我们常见的便于理解的N维数组仅仅是“逻辑视图”，它们不过是包装出来的。
一个N维数组就是一个通用的同类数据容器，也就是说它包含的每个元素数据类型均相同。每个数组的维度（dimension)都由一个 ndim 属性来描述。

import numpy as np # 导入 numpy
my_array = np.arange(1, 10) # 创建一个一维数组

my_array.ndim
print(my_array)

shape

对于N维数组而言，它还有一个重要的属性一shape(数组的形状)。

形状主要用来表征数组每个维度的数量。一维数组的形状就是它的长度，有时候，一维数组也被称为lD张量0(1D Tensor).

 

import numpy as np # 导入 numpy
my_array = np.arange(1, 10) # 创建一个一维数组


print(my_array)
print(my_array.shape)  

张量

张量(Tensor)是矩阵在任意维度上的推广，张量的维度通常称为轴（axis)。 0D张量：只包括一个数字的张量，如常数、3或3.14。 1D张量：一维数组，也称为向量，如[1,2,3]。 2D张量：二维数组，也称为矩阵，如[[3，6]，[9,12]] 3D张量及更高维张量：多个矩阵(2D张量)可构造成一个新的3D张量，如[[[1,1,1]，[2,2,2]，[3,3,3]，[4,4,4]]]。

多个3D张量可以构造成一个4D张量，以此类推。在表达上，张量方括号的层次有多深，就表示这是多少维张量。

reshape()

在上述代码中，处查看了一维数组的形状信息（即向量的尺寸)，其输出结果为数组的长度。但NumPy数组形状并不是一成不变的，可以通过 reshape()方法将原有数组进行“重构”（变形）

b = np.arange(15) # 创建15个元素的一维数组
print(b)

b = b.reshape(3, 5) # 改变数组形状为 3 行 5 列
print(b)

print(b.ndim)# 查看维度
print(b.shape) # 数组的形状
print(b.size) # 查看数组元素的总个数

在 reshape() 重构操作，把一个一维数组转换成了一个二维数组，输出了形状。在这个形状信息中，第一个数字表示行数，第二个数字表示列数，二维数组也被称为2D张量。

我们通过重构操作，把一个一维数组转换成了一个二维数组，在这个形状信息中，第一个数字表示行数，第二个数字表示列数。有时，二维数组也被称为2D张量。

3D

这里需要注意的是，NumPy表示三维数组维度信息的方式和我们通常的认知稍有不同。

比如，我们想创建两个3行5列的数组，它的形状参数为(2,3,5)，而不是(3,5,2)，如图6所示。通常三维数组也被称为3D张量，以此类推。

 

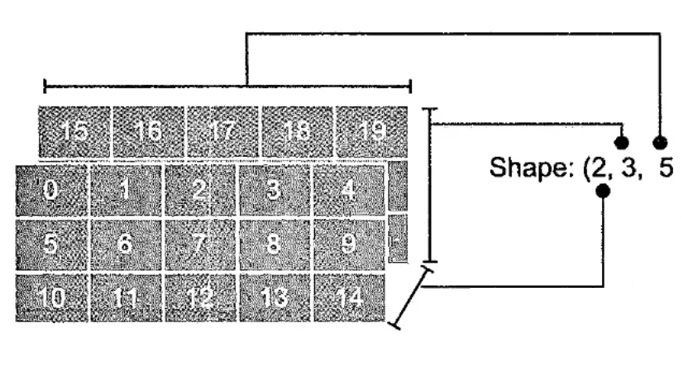
 一个小正方形也可以是三维数组，一排4*3的也可以看成是三维数组。这两种情况而言，三维数组的第三个参数不太一样而已，是1.

a = np.arange(30).reshape(2,3,5) # 重构数组为2 通道 3行5列
print(a)

[[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]

[[15 16 17 18 19]
[20 21 22 23 24]
[25 26 27 28 29]]]

 

a=np.array([1,2,3])
print(a.ndim)
b=np.array([[1,2,3],[4,5,6]])
print(b.ndim)

 

只要是[]中括号嵌套三层的，那么就是三维数组，否则就不是。

当然嵌套在最内层的，可以是一个元素的数组，就是一个。假如是好几个，就相当于上面的图中的一层元素的每一排。