概率与期望
概率:
注:概率一般用P来表示
一些公式:
- \(P(样本空间-A)=1-P(A)\)
\(P(A∪B)=P(A)+P(B)-P(A∩B)\)
\(A∩B=∅,则P(A∪B)=P(A)+P(B)\)
0.关于事件之间的关系(一些定义):
- 事件之间相互影响,即A发生后B发生的概率会发生影响。
如在平时我们旅游的概率为1%,但是到了放假时我们旅游的概率会显著上升,而开学后毫无疑问会接近0%,同样我们旅游时开学的概率是0。 - 与相互影响相反的是这些事件发生概率始终如一,称之为独立事件,举个例子,我们有两个硬币,掷第一个后再掷第二个,第二个正面向上概率是50%,与只掷第二个,第二个正面向上的概率一致,这种是不相互影响。
- 互斥则是一个事件发生,另一个事件必然不发生,比方说去旅游,我们可以去杭州或重庆或泰安,这几个只能选其一。在互斥中有一类特殊的是对立事件,就是这两个事件只能选一个且必须选一个,比如我们旅游是出国或不出国,只有这两种。
- 根据以上定义,我们可以得出,互斥事件一定不是独立事件,独立事件一定不是互斥事件(只要这些事件都有可能发生)。
- 同时互斥事件不一定是对立事件,对立事件一定是互斥事件,这个是显然的。
- 基本事件就是一组事件满足这些事件互不影响且互斥。
- 注意\(A∪B=∅\)时,二者不一定互斥,因为其中之一的概率为0时也满足(其实可以忽略这种情况,因为没有概率发生的事件我要它干嘛)
- 完备事件组,即为一个事件组中所有的事件间均互斥,且概率相加总和为1。
1.条件概率:
如果A发生了,那么B发生的概率记作P(B|A)
考虑四种情况:
- P(AB都发生)=a,P(AB都不发生)=b
P(只有A发生)=c,P(只有B发生)=d
那么\(P(B|A)=a/(a+c)\),即\(P(B|A)=P(A∪B)/P(A)\)
2.全概率&&贝叶斯公式:
全概率公式:
已知一个完备事件组A,将在事件组A的各个事件分支i下发生事件B的概率记为\(P(B|A_i)\)
那么\(P(B|A)=Σ^i_{A的分支数}P(A_i)×P(B|A_i)\)
这里可以看出全概率就是算出一个事件在一个事件组发生的背景下发生的概率。
贝叶斯公式:
依旧是上述已知条件,要求我们求\(P(A_i|B)\)(这里要注意,B为已发生事件,可以认为其概率为1,就是一个完备事件组)
那么我们已经有了B在事件组A下发生的概率(全概率公式得来)为\(P(B|A)\)
\(P(A_i|B)=P(B|A_i)×P(A_i)/P(B|A)\)
期望:
不同于其余数学专题的东西那么多变,这玩意一般都用于dp.
大致说一下期望的意思,对于一个问题,我们可能得到的所有答案进行一个带权的平均(这个权值就是概率)所得到的值
比方说我们从家到学校有4条路,如图。
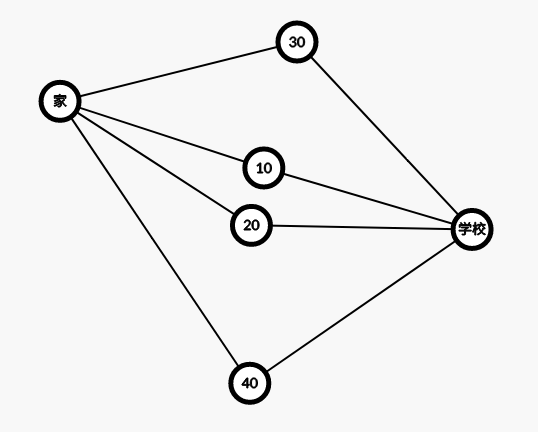
然后我们由于各式各样的原因,走某一条路的概率如下图。
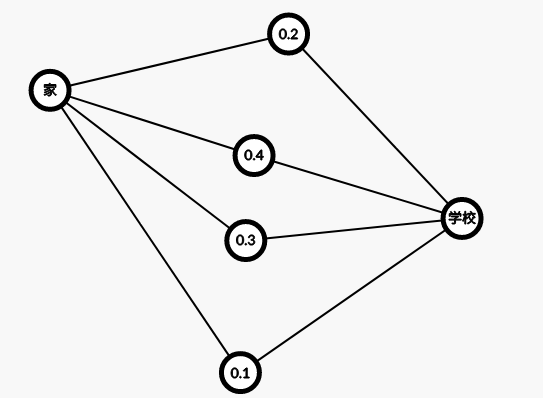
设走各个路的概率为\(P_i\),路的长度为\(W_i\),\(n\)为路径数那么我们计算出从家到学校距离的期望\(E\)为
将路抽象为事件,边权抽象为事件对应结果,这样我们的期望就能在许多题目中应用。
(这里的路的选择是一个完备事件组,我的短期理解是期望都是一个一个完备事件组之间的选择转移,这样方便dp)
板子题绿豆蛙:
与先前所述一致,这是一道典型的期望dp题目,比较简单,因为我们知道了终点的位置,且图是有向无环图。
由于期望的线性性,可以从终点向起点开始dp,但是我们用记搜来模拟,更加方便。
设w[]表示每个边的长度,out[]为点的出度
状转就是\(E_i=Σ^k_{out[i]}1/out[i]×(E_k+w[i->k])\)
#include<bits/stdc++.h>
#define ll long long
#define qr qr()
#define pa pair<int,int>
#define fr first
#define sc second
#define lc tree[rt].ls
#define rc tree[rt].rs
using namespace std;
const int N=2e5+200;
map <int,int> mp;
int n,m,num[N],tot,head[N],out[N];
double f[N];
struct node{
int t,w,nx;
}edge[N];
struct What_can_I_say{
int ls,rs,l,r,mx;
}tree[N<<2];
inline int qr
{
int x=0;char ch=getchar();bool f=0;
while(ch>57||ch<48)
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch<=57&&ch>=48)x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return f?-x:x;
}
void add(int f,int t,int w)
{
edge[++tot]={t,w,head[f]};
++out[f];
head[f]=tot;
}
double dp(int now)
{
if(f[now])return f[now];
for(int i=head[now];i;i=edge[i].nx)
{
int t=edge[i].t;
f[now]+=1.0/out[now]*(edge[i].w+dp(t));
}
return f[now];
}
void init()
{
n=qr,m=qr;
for(int i=1;i<=m;++i)
{
int f=qr,t=qr,w=qr;
add(f,t,w);
}
printf("%.2lf",dp(1));
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
init();
return 0;
}
略微进阶一点点的一道题目是聪聪与可可。
相对也较简单,很明显每个点到每个点决策唯一,是最短路的对应决策,一次行动是猫先开始,所以除非边界,这猫必然跳两步。
所以状转是很简单的,设猫在i,鼠在j,k表示当前边序号,out[]为点的出度,t[]为某个边所到的节点,
f[i][j]表示从点i到点j的一个期望值(我们还是用记搜,因为dp在外部不太方便模拟),ds[i][j]为猫的决策。
那么\(f[i][j]=(i==j)?0:(ds[i][j]==j)?1:Σ^k_{out[j]}1/out[j]×f[ds[i][j]][t[k]]\)
看上去较复杂,但是思路清晰是非常容易想到的(尤其在打完绿豆蛙后)。
唯一要注意的点在于,我们在决定决策时,要存储对应策略的第一步节点落在哪里,便于决策更新(题目中说了,相同方案时猫走节点编号小的点),就这样就行了。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
#define qr qr()
#define pa pair<int,int>
#define fr first
#define sc second
#define lc tree[rt].ls
#define rc tree[rt].rs
using namespace std;
const int N=2e5+200,MN=1e3+20;
int n,m,st,ed,tot,head[MN],ds[MN][MN],fr[MN][MN],dis[MN],out[MN];
double f[MN][MN];
struct node{
int t,nx;
}edge[N];
inline int qr
{
int x=0;char ch=getchar();
while(ch>57||ch<48)ch=getchar();
while(ch<=57&&ch>=48)x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x;
}
void add(int f,int t)
{
edge[++tot]={t,head[f]};
++out[f];
head[f]=tot;
}
void djs(int now)
{//其实是bfs...想到一半发现不用优先队列.
queue <int> q;
memset(dis,0,sizeof(dis));
q.push(now);
ds[now][now]=now;
while(!q.empty())
{
int p=q.front();
q.pop();
for(int i=head[p];i;i=edge[i].nx)
{
int t=edge[i].t;
if(!dis[t])
{
dis[t]=dis[p]+1;
if(!dis[p])fr[now][t]=t;
else fr[now][t]=fr[now][p];
if(dis[p]<=1)ds[now][t]=t;
else ds[now][t]=ds[now][p];
q.push(t);
}
else if((dis[p]==dis[t]-1)&&(fr[now][t]>fr[now][p]||(fr[now][t]==fr[now][p]&&ds[now][t]>ds[now][p])))
{
if(dis[t]>2)ds[now][t]=ds[now][p];
fr[now][t]=fr[now][p];
}
}
}
}
double dp(int nst,int ned)
{
// cout<<nst<<' '<<ned<<endl;
if(f[nst][ned])return f[nst][ned];
if(nst==ned)return 0;
if(ds[nst][ned]==ned)return 1;
int tmp=ds[nst][ned];
for(int i=head[ned];i;i=edge[i].nx)
{
int t=edge[i].t;
f[nst][ned]+=1.0/(out[ned]+1)*(1+dp(tmp,t));
}
f[nst][ned]+=1.0/(out[ned]+1)*(1+dp(tmp,ned));
return f[nst][ned];
}
void init()
{
n=qr,m=qr;
st=qr,ed=qr;
int f,t;
for(int i=1;i<=m;++i)
{
f=qr,t=qr;
add(f,t);
add(t,f);
}
for(int i=1;i<=n;++i) djs(i);
printf("%.3lf",dp(st,ed));
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
init();
return 0;
}
相较上面这个题,OSU这个题事实上是更有启发性意义的。
我们在dp中真正要去得到的关键是转移方程,在这里也一样,毕竟期望dp就是一种dp。
那么这个题很明显是dp,关键是如何维护信息便于期望转移。
思考我们加入一个数对答案的影响,假设之前已经选入x个连续的1。
那么明显这部分答案会由\(x^3\)更新为\((x+1)^3\)。
因为我们是dp转移,所以只会得到前一个位数的期望值。
但是我们将\((x+1)^3\)展开,\((x+1)^3=x^3+3x^2+3x+1\)
可见更新答案时我们还需要两个量,一个是\(x^2\)的期望,一个是\(x\)的期望。
把\((x+1)^2\)展开\((x+1)^2=x^2+2x+1\)
所以我们可以用前一个答案存储的\(x^3,x^2,x\)的期望完成转移。
要强调的是我们不能只维护一个\(x\)的期望去转移其他项,因为我们在进行期望转移时必然乘概率,如果用其平方相当于概率被乘了两次。
期望的线性性真神奇
#include<bits/stdc++.h>
#define ll long long
#define qr qr()
#define pa pair<int,int>
#define fr first
#define sc second
#define lc tree[rt].ls
#define rc tree[rt].rs
using namespace std;
const int N=2e5+200;
ll n,num[N],tot,head[N];
long double suc[N],x1[N],x2[N],x3[N];
//x3其实不准确,我们维护的是答案,而不是x^3的期望值,因为每一次我们的答案都要将对应的x^3的期望叠加上来,是各个位上的期望的叠加。但都写上了,就先这样。
struct node{
int t,w,nx;
}edge[N];
struct What_can_I_say{
int ls,rs,l,r,mx;
}tree[N<<2];
inline int qr
{
int x=0;char ch=getchar();bool f=0;
while(ch>57||ch<48)
{
if(ch=='-')f=1;
ch=getchar();
}
while(ch<=57&&ch>=48)x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return f?-x:x;
}
void add(int f,int t,int w)
{
edge[++tot]={t,w,head[f]};
head[f]=tot;
}
void init()
{
n=qr;
for(int i=1;i<=n;++i)scanf("%llf",&suc[i]);
for(int i=1;i<=n;++i)
{
x1[i]=(x1[i-1]+1)*suc[i];
x2[i]=(x2[i-1]+2*x1[i-1]+1)*suc[i];
x3[i]=x3[i-1]+(3*x2[i-1]+3*x1[i-1]+1)*suc[i];
}
printf("%.1llf",x3[n]);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("in.in","r",stdin);
freopen("out.out","w",stdout);
#endif
init();
return 0;
}


