Nordic Collegiate Programming Contest 2015(第七场)
A:Adjoin the Networks
He has asked you to use as few cables as possible, but the length of the cables used does not matter to him, since the cables are optical and the connectors are the expensive parts. Your boss is rather picky on cable usage, so you know that the already existing networks have as few cables as possible.
Due to your humongous knowledge of computer networks, you are of course aware that the latency for an information packet travelling across the network is proportional to the number of hops the packet needs, where a hop is a traversal along a single cable. And since you believe a good solution to your boss' problem may earn you that long wanted promotion, you decide to minimise the maximum number of hops needed between any pair of network nodes.
Input Format
On the first line, you are given two positive integers, the number 1≤c≤105 of computers and the number 0≤l≤c−1of existing cables. Then follow lll lines, each line consisting of two integers a and b, the two computers the cables connect. You may assume that every computer has a unique name between 0 and n−1.
Output Format
The maximum number of hops in the resulting network.
样例输入1
6 4
0 1
0 2
3 4
3 5
样例输出1
3
样例输入2
11 9
0 1
0 3
0 4
1 2
5 4
6 4
7 8
7 9
7 10
样例输出2
4
最后要与最大联通块的直径比较。
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; typedef pair<int,int> P; vector<int>v[100006]; int vis[100006][3]; int n,m; int dis[100006],a[100006]; int ans,_,pos; void dfs(int u,int d,int k) { dis[u]=d; if(dis[u]>ans) { ans=dis[u]; _=u; } for(auto t:v[u]) { if(!vis[t][k]) { vis[t][k]=1; dfs(t,d+1,k); } } } bool cmp(int x,int y){ return x>y; } int main() { scanf("%d%d",&n,&m); for(int i=0,x,y;i<m;i++) { scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); vis[x][2]=1; vis[y][2]=1; } int cnt=0; pos=-1; for(int i=0;i<n;i++) { if(!vis[i][0] && vis[i][2]){ ans=-1; vis[i][0]=1; dfs(i,0,0); ans=-1; vis[_][1]=1; dfs(_,0,1);//求树的直径 //printf("%d\n",ans); pos=max(ans,pos); a[cnt++]=(ans+1)>>1; } } sort(a,a+cnt,cmp); if(n==1)printf("0\n"); else if(n==2) printf("1\n"); else if(!cnt) printf("2\n"); else if(cnt>=3 && a[0]==a[2]) printf("%d\n",max(pos,a[0]+a[1]+2)); else printf("%d\n",max(pos,a[0]+a[1]+1)); return 0; }
B:Bell Ringing
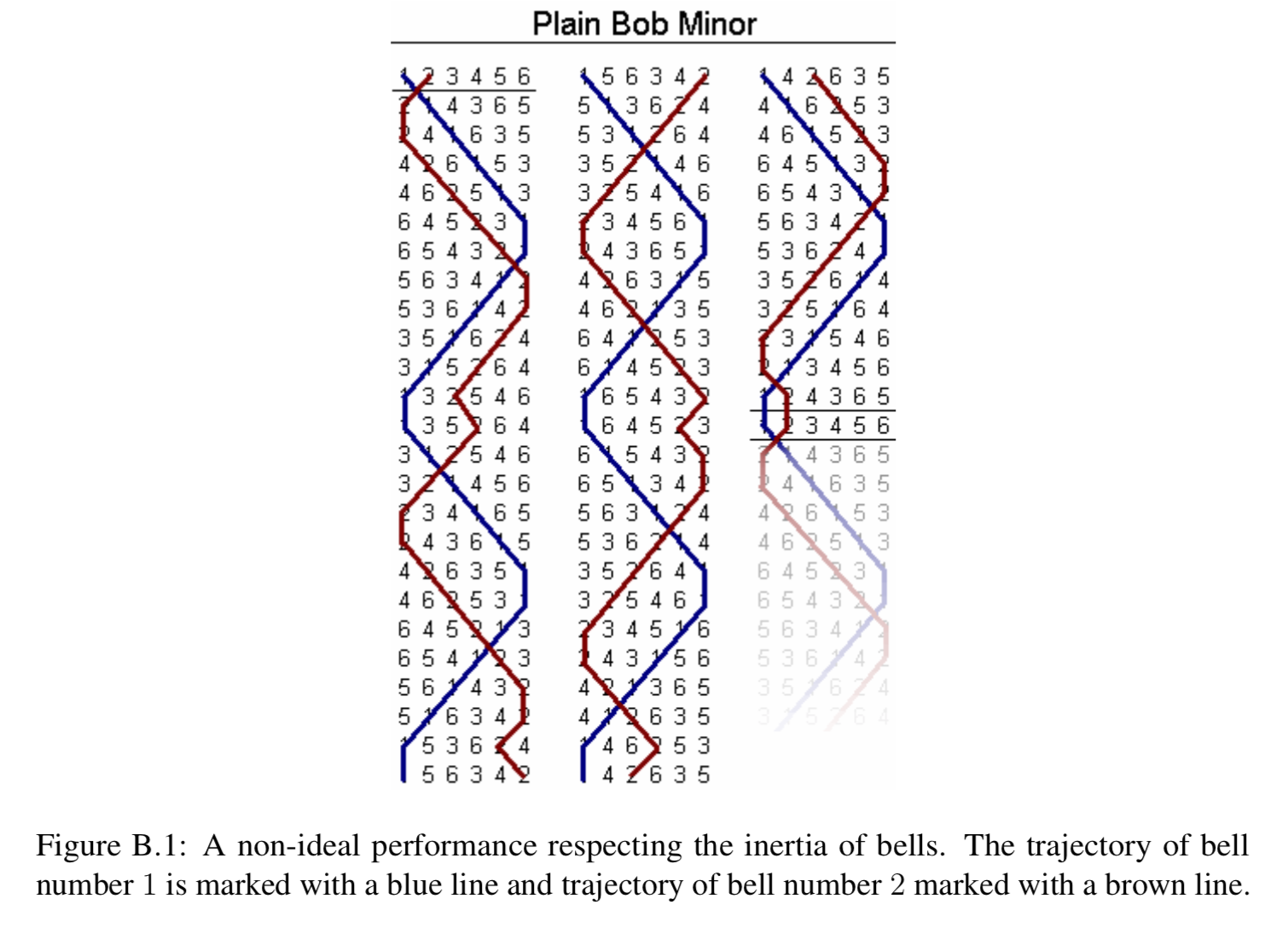
Method ringing is used to ring bells in churches, particularly in England. Suppose there are 6 bells that have 6 different pitches. We assign the number 1 to the bell highest in pitch, 2 to the second highest, and so on. When the 6 bells are rung in some order—each of them exactly once—it is called a row. For example, 1, 2, 3, 4, 5, 6 and 6, 3, 2, 4, 1, 5 are two different rows.
An ideal performance contains all possible rows, each played exactly once. Unfortunately, the laws of physics place a limitation on any two consecutive rows; when a bell is rung, it has considerable inertia and the ringer has only a limited ability to accelerate or retard its cycle. Therefore, the position of each bell can change by at most one between two consecutive rows.
In Figure ??, you can see the pattern of a non-ideal performance, where bells only change position by at most one.
Given nnn, the number of bells, output an ideal performance. All possible rows must be present exactly once, and the first row should be 1,2,⋯,n.
Input Format
The first and only line of input contains an integer n such that 1≤n≤8.
Output Format
Output an ideal sequence of rows, each on a separate line. The first line should contain the row 1,2,⋯,n and each two consecutive lines should be at most 1 step away from each other. Each row should occur exactly once in the output.(No extra space at the end of each line)
本题答案不唯一,符合要求的答案均正确
样例输入
2
样例输出
1 2 2 1
题目要求只有两点,要求1:要把n个数的全排列打印出来,要求2:相邻的两层数满足同一个数字的位置变化之多一个单位
比如说 1 2 3 与 1 3 2这样是符合题意的但是1 2 3 与3 1 2是不行的因为3的位置变了两个单位同理 1 2 3与2 3 1也不符合题意。
这是一到递归题,n个数的全排列可以有n-1个数的全排列里面插入第n个数得到,同时我们只要控制插入的顺序就可以保证满足要求
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; int a[50006][10],n,l,r; void solve() { l=r=0;a[0][0]=1; for(int i=2;i<=n;i++) { int len=r; for(int j=l;j<=r;j++) { if((j-l)&1){ for(int t=0;t<i;t++) { len+=1; for(int k=0;k<t;k++) a[len][k]=a[j][k]; a[len][t]=i; for(int k=t+1;k<i;k++) a[len][k]=a[j][k-1]; } } else{ for(int t=i-1;t>=0;t--){ len+=1; for(int k=0;k<t;k++) a[len][k]=a[j][k]; a[len][t]=i; for(int k=t+1;k<i;k++) a[len][k]=a[j][k-1]; } } } l=r+1; r=len; } } int main() { scanf("%d",&n); solve(); for(int i=l;i<=r;i++) for(int j=0;j<n;j++) printf("%d%c",a[i][j],j==n-1?'\n':' '); return 0; }
C:Cryptographer's Conundrum
The walls of the corridors at the Theoretical Computer Science group (TCS) at KTH are all but covered with whiteboards. Some of the faculty members are cryptographers, and like to write cryptographic puzzles on the whiteboards. A new puzzle is added whenever someone discovers a solution to the previous one.
When Per walked in the corridor two weeks ago, he saw that the newest puzzle read "GuvfVfNGrfg". After arriving at his computer, he quickly figured out that this was a simple ROT13 encryption of "ThisIsATest".
The series of lousy puzzles continued next week, when a new puzzle read Photo by Alan Wu "VmkgdGFyIHPDpGtlcmhldGVuIHDDpSBzdMO2cnN0YSBhbGx2YXIK". This was just base64-encoded text! "Enough with these pranks", Per thought; "I'm going to show you!"
Now Per has come up with a secret plan: every day he will erase one letter of the cipher text and replace it with a different letter, so that, in the end, the whole text reads "PerPerPerPerPerPerPer". Since Per will change one letter each day, he hopes that people will not notice.
Per would like to know how many days it will take to transform a given cipher text into a text only containing his name, assuming he substitutes one letter each day. You may assume that the length of the original cipher text is a multiple of 3.
For simplicity, you can ignore the case of the letters, and instead assume that all letters are upper-case.
Input Format
The first and only line of input contains the cipher text on the whiteboard. It consists of at most 300 upper-case characters, and its length is a multiple of 3.
Output Format
Output the number of days needed to change the cipher text to a string containing only Per's name.
样例输入
SECRET
样例输出
4
签到题
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; char s[306]; map<int,char>m; int main() { m[0]='P'; m[1]='E'; m[2]='R'; while(scanf("%s",&s)!=EOF) { int ans=0; for(int i=0;s[i];i++) if(s[i]!=m[i%3]) ans++; printf("%d\n",ans); } return 0; }
D:Disastrous Downtime
You're investigating what happened when one of your computer systems recently broke down. So far you've concluded that the system was overloaded; it looks like it couldn't handle the hailstorm of incoming requests. Since the incident, you have had ample opportunity to add more servers to your system, which would make it capable of handling more concurrent requests. However, you've simply been too lazy to do it—until now. Indeed, you shall add all the necessary servers . . . very soon!
To predict future requests to your system, you've reached out to the customers of your service, asking them for details on how they will use it in the near future. The response has been pretty impressive; your customers have sent you a list of the exact timestamp of every request they will ever make!
You have produced a list of all the nnn upcoming requests specified in milliseconds. Whenever a request comes in, it will immediately be sent to one of your servers. A request will take exactly 100010001000 milliseconds to process, and it must be processed right away.
Each server can work on at most kkk requests simultaneously. Given this limitation, can you calculate the minimum number of servers needed to prevent another system breakdown?
Input Format
The first line contains two integers 1≤n≤100000and 1≤k≤100000, the number of upcoming requests and the maximum number of requests per second that each server can handle.
Then follow nnn lines with one integer 0≤ti≤1000000each, specifying that the iii-th request will happen tit_iti milliseconds from the exact moment you notified your customers. The timestamps are sorted in chronological order. It is possible that several requests come in at the same time.
Output Format
Output a single integer on a single line: the minimum number of servers required to process all the incoming requests, without another system breakdown.
样例输入1
2 1 0 1000
样例输出1
1
样例输入2
3 2 1000 1010 1999
样例输出2
2
一个数可能包含在他的前1000ms或者后1000ms内
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; int n,m,a[101005]; int main() { scanf("%d%d",&n,&m); for(int i=0,x;i<n;i++){ scanf("%d",&x); a[x]++; } int ans=0; for(int i=0;i<100000;i++){ for(int j=i+1;j<i+1000;j++) a[i]+=a[j]; ans=max(ans,a[i]); } printf("%d\n",ans/m+(ans%m?1:0)); return 0; }
E:Entertainment Box
The three friends wonder how many TV shows they can record during one day. They provide you with the TV guide for today's shows, and tell you the number of shows the machine can record simultaneously. How many shows can they record, using their recording machine? Count only shows that are recorded in their entirety.
Input Format
The first line of input contains two integers n, k (1≤k<n≤100000). Then follow nnn lines, each containing two integers xi,yi, meaning that show iii starts at time xix_ixi and finishes by time yiy_iyi. This means that two shows iii and jjj, where yi=xjy_i = x_jyi=xj, can be recorded, without conflict, in the same recording slot. You may assume that 0≤xi<yi≤10000000000.
Output Format
The output should contain exactly one line with a single integer: the maximum number of full shows from the TV guide that can be recorded with the tape recorder.
样例输入1
3 1
1 2
2 3
2 3
样例输出1
2
样例输入2
4 1
1 3
4 6
7 8
2 5
样例输出2
3
样例输入3
5 2
1 4
5 9
2 7
3 8
6 10
样例输出3
3
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; multiset<int>s; multiset<int>::iterator it; int n,k; struct node { int x,y; bool operator<(const node &a)const{ return a.y==y?a.x<x:a.y>y; } }e[100005]; int main() { scanf("%d%d",&n,&k); for(int i=0;i<n;i++) scanf("%d%d",&e[i].x,&e[i].y); sort(e,e+n); for(int i=0;i<k;i++) s.insert(0); int ans=0; for(int i=0;i<n;i++) { it=s.upper_bound(e[i].x); if(it==s.begin()) continue; it--; s.erase(it); s.insert(e[i].y); ans++; } printf("%d\n",ans); return 0; }
G:Goblin Garden Guards
In an unprecedented turn of events, goblins recently launched an invasion against the Nedewsian city of Mlohkcots. Goblins—small, green critters—love nothing more than to introduce additional entropy into the calm and ordered lives of ordinary people. They fear little, but one of the few things they fear is water.
The goblin invasion has now reached the royal gardens, where the goblins are busy stealing fruit, going for joyrides on the lawnmower and carving the trees into obscene shapes, and King Lrac Fatsug has decreed that this nonsense stop immediately!
Thankfully, the garden is equipped with an automated sprinkler system. Enabling the sprinklers will soak all goblins within range, forcing them to run home and dry themselves.
Serving in the royal garden guards, you have been asked to calculate how many goblins will remain in the royal garden after the sprinklers have been turned on, so that the royal gardeners can plan their next move.
Input Format
The input starts with one integer 1≤g≤100000, the number of goblins in the royal gardens.
Then, for each goblin follows the position of the goblin as two integers, 0≤xi≤100000 and 0≤yi≤100000. The garden is flat, square and all distances are in meters. Due to quantum interference, several goblins can occupy exactly the same spot in the garden.
Then follows one integer 1≤m≤20000, the number of sprinklers in the garden.
Finally, for each sprinkler follows the location of the sprinkler as two integers 0≤xi≤100000 and 0≤yi≤100000, and the integer radius 1≤r≤100 of the area it covers,meaning that any goblin at a distance of at most rrr from the point (xi,yi) will be soaked by this sprinkler. There can be several sprinklers in the same location.
Output Format
Output the number of goblins remaining in the garden after the sprinklers have been turned on.
样例输入
5
0 0
100 0
0 100
100 100
50 50
1
0 0 50
样例输出
4
计算几何问题,所有的点都小于10000,半径不超过100,则每次可暴力枚举圆心所处的正方形内的点
但不知道怎么回事,写炸了好几次,检查不出来,看来还是代码习惯不好。
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #pragma GCC diagnostic error "-std=c++11" #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define esp 1e-9 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 1044266560 #define mem(a) (memset(a,0,sizeof(a))) int dcmp(double x){return fabs(x)<esp?0:x<0?-1:1;} typedef long long ll; int n,m; struct Point{ int x,y; }p[100005]; bool vis[10006][10006]; int main() { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%d%d",&p[i].x,&p[i].y); scanf("%d",&m); for(int i=0,x,y,r;i<m;i++) { scanf("%d%d%d",&x,&y,&r); for(int i=max(0,x-r);i<=min(10000,x+r);i++) for(int j=max(0,y-r);j<=min(10000,y+r);j++) if(((i-x)*(i-x))+((j-y)*(j-y))<=r*r) vis[i][j]=1; } int ans=0; for(int i=0;i<n;i++) if(!vis[p[i].x][p[i].y]) ans++; printf("%d\n",ans); return 0; }






 浙公网安备 33010602011771号
浙公网安备 33010602011771号