计算几何知识点简记

什么是计算几何

　　由函数逼近论、微分几何、代数几何、计算数学等形成的边缘学科，研究几何形体的计算机表示、分析和综合。它是计算机图形学、计算机辅助设计的数学基础。

笛卡尔坐标系点，边的定义以及基础运算

struct Point{
    double x,y;
    Point(){}
    Point(const double &a,const double &b):x(a),y(b){}
};
struct Lineseg{
    Point s,e;
    Lineseg(){}
    Lineseg(const Point &a,const Point &b):s(a),e(b){}
};
Point operator + (Point a,Point b) {return Point(a.x+b.x,a.y+b.y);}
Point operator - (Point a,Point b) {return Point(a.x-b.x,a.y-b.y);}
Point operator * (Point a,double x){return Point(a.x*x,a.y*x);}
Point operator / (Point a,double x){return Point(a.x/x,a.y/x);}
bool  operator < (const Point &a,const Point &b){return a.x<b.x|| (a.x==b.x) && a.y<b.y;}
bool  operator ==(const Point &a,const Point &b){return !dcmp(a.x-b.x) && !dcmp(a.y-b.y);}
bool  operator !=(const Point &a,const Point &b){return !(a==b);}
double operator * (Point a,Point b){return a.x*b.y-a.y*b.x;}//向量叉积

 

矢量的概念

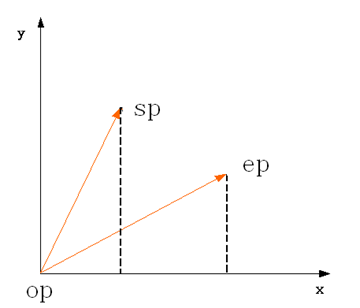
　　如果一条线段的端点是有次序之分的，我们把这种线段称为有向线段(directed segment)。如果有向线段p1p2的起点p1 在坐标原点，我们可以把这个有向线段称为矢量(vector)p2。

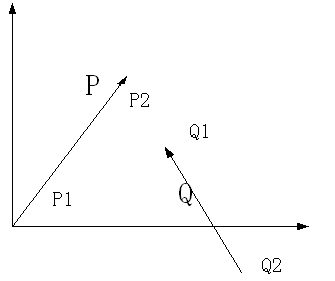
向量Q=Q1-Q2

设二维矢量P = ( x1, y1 )，Q = ( x2 , y2 )
则矢量加法定义为： P + Q = ( x1 + x2 , y1 + y2 )
矢量减法定义为： P - Q = ( x1 - x2 , y1 - y2 )。
显然有性质 P + Q = Q + P，P - Q = - ( Q - P )。

矢量叉积

　　矢量叉积是与直线和线段相关算法的核心部分

　　定义：设矢量P = ( x1, y1 )，Q = ( x2, y2 )，
  　　则P × Q = x1*y2 - x2*y1

  　 几何意义：矢量叉积为由(0,0)、p1、p2和p1+p2所组成的平行四边形的带符号的面积，其结果是一个标量。显然有性质 P × Q = - ( Q × P ) 和 P × ( - Q ) = - ( P × Q )。

　　|P×Q|=|P|×|Q|sinθ

　　|P×Q|等于以P和Q为两边的平行四边形的面积

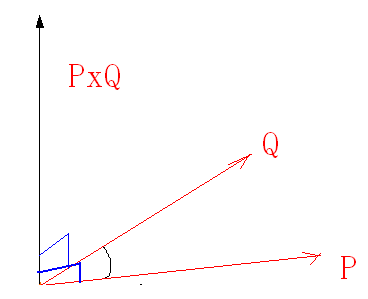
叉积的几何意义

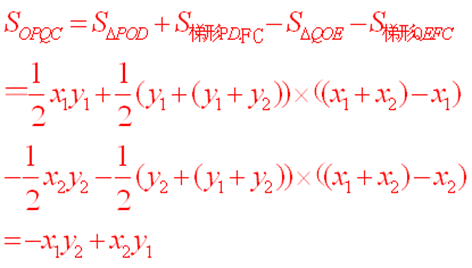
double operator * (Point a,Point b){return a.x*b.y-a.y*b.x;}//向量叉积
double multiply(Point a,Point b,Point c){
    return (b-a)*(c-a);
}

 

矢量叉积的作用

通过符号判断两矢量之间相互之间的顺时针关系（右手螺旋定理）

若 P × Q > 0 , 则P在Q的顺时针方向。
若 P × Q < 0 , 则P在Q的逆时针方向。
若 P × Q = 0 , 则P与Q共线，但可能同向也可能反向

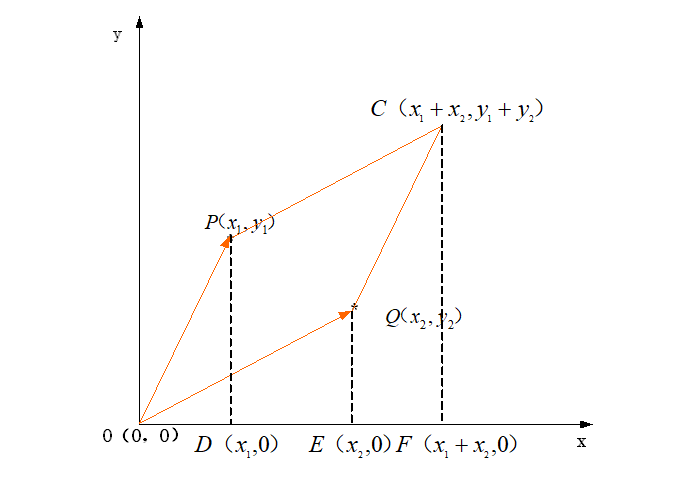
计算多边形面积

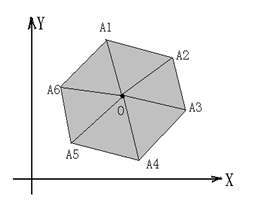
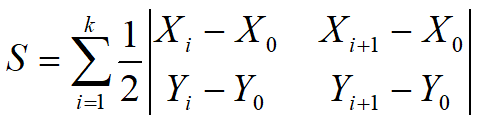
化简可得

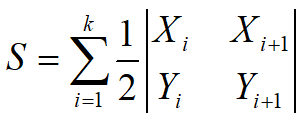
double area(int n)//求面积//要求是凸多边形，且坐标点逆时针排列
{
    double s=0.0;
    for(int i=0;i<n;i++)
        s+=p[i]*p[(i+1)%n];
    return s/2.0;
}

 

矢量叉积的作用-判断凹凸多边形

 　　把多边形的任何一条边向两方延长，如果多边形的其他各边都在延长所得直线的同一旁，这样的多边形叫做凸多边形
方法：

　　只需依次计算多边形相邻两边矢量的叉积
　　　　(1)全部为零，则多边形各边共线；
　　　　(2)部分为正，部分为负，则为凹多边形；
　　　　(3)全部大于零或等于零，则为凸多边形；
　　　　(4)全部小于零或等于零，则为凸多边形。

矢量叉积的作用-折线段的拐向判断

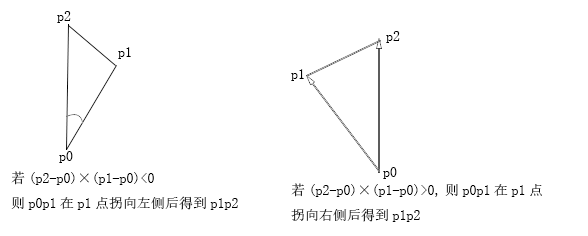
折线段的拐向判断方法可以直接由矢量叉积的性质推出。对于有公共端点的线段p0p1和p1p2，通过计算(p2 - p0) × (p1 - p0)的符号便可以确定折线段的拐向：
　　若(p2 - p0) × (p1 - p0) > 0,则p0p1在p1点拐向右侧后得到p1p2。
　　若(p2 - p0) × (p1 - p0) < 0,则p0p1在p1点拐向左侧后得到p1p2。
　　若(p2 - p0) × (p1 - p0) = 0,则p0、p1、p2三点共线。

矢量叉积的作用-判断点是否在线段上

　　设点为Q，线段为P1P2 ，判断点Q在该线段上的依据是：( Q - P1 ) × ( P2 - P1 ) = 0 且 Q 在以 P1，P2为对角顶点的矩形内。前者保证Q点在直线P1P2上，后者是保证Q点不在线段P1P2的延长线或反向延长线上

bool online(Lineseg l,Point p){//判断点是否在线上
    return multiply(l.s,p,l.e)==0 && (p.x-l.s.x)*(p.x-l.e.x)<=0 && (p.y-l.s.y)*(p.y-l.e.y)<=0;
}

矢量叉积的作用-判断两直线相交

快速排除法

　　设以线段 P1P2 为对角线的矩形为R， 设以线段 Q1Q2 为对角线的矩形为T，如果R和T不相交，显然两线段不会相交。

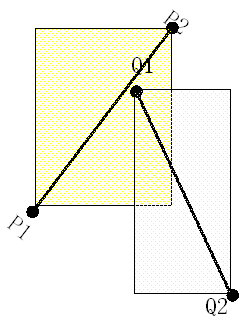
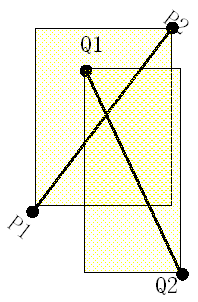
跨立实验

如果两线段相交则两线段必然相互跨立对方。

当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上。

所以判断P1P2跨立Q1Q2的依据是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。
同理判断Q1Q2跨立P1P2的依据是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0。

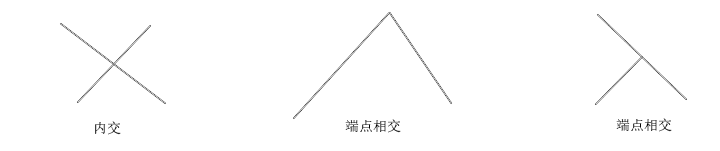
//判断两线段是否相交，内交或者端点相交返回true
bool intersect(Lineseg u,Lineseg v)
{
    return 
    (max(u.s.x,u.e.x)>=min(v.s.x,v.e.x)) &&
    (max(v.s.x,v.e.x)>=min(u.s.x,u.e.x)) &&
    (max(u.s.y,u.e.y)>=min(v.s.y,v.e.y)) &&
    (max(v.s.y,v.e.y)>=min(u.s.y,u.e.y)) &&//快速排斥实验
    (multiply(u.s,v.s,u.e)*multiply(u.s,u.e,v.e))>=0 &&//跨立实验//注意顺序
    (multiply(v.s,u.s,v.e)*multiply(v.s,v.e,u.e))>=0;
}
//判断u和v相交，且交点不是端点
bool intersect_A(Lineseg u,Lineseg v)
{
    return intersect(u,v)&&
           (!(online(u,v.s)))&&
           (!(online(u,v.e)))&&
           (!(online(v,u.s)))&&
           (!(online(v,u.e)));
}
bool intersect_L(Lineseg u,Lineseg v)//判断线段v是否跨立u所在的直线
{
    return multiply(u.s,v.s,u.e)*multiply(u.s,u.e,v.e)>=0;
}

矢量叉积-判断点与多边形的关系

 射线法

　　从目标点出发 ， 向某一方向发出一条射线 ， 如果该射线和四边形交点个数是奇数，则该点在四边形内部，若为偶数，则不在内部。

　　做射线L的方法是：设P'的纵坐标和P相同，横坐标为正无穷大（很大的一个正数），则P和P'就确定了射线L。

　　同时要注意特殊情况。

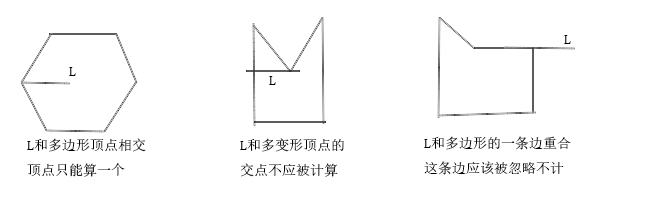
//射线法判断点Q与多边形polygon的位置关系，要求polygon是简单多边形，顶点逆时针排列
//如果点在多边形内返回2，点在多边形上返回1，点在多边形外返回0
int insidepolygon(int n,Point polygon[],Point p)
{
    int num=0,i;//n为顶点数
    Lineseg line;
    if(n==1) return ((fabs(polygon[0].x-p.x)<esp) && (fabs(polygon[0].y-p.y)<esp));
    else if(n==2)
    {
        Lineseg side;
        side.s=polygon[0];
        side.e=polygon[1];
        return online(side,p);
    }
    line.s=p;
    line.e.y=p.y;
    line.e.x=INF;
    for(int i=0;i<n;i++)
    {
        Lineseg side;
        side.s=polygon[i];
        side.e=polygon[(i+1)%n];
        if(online(side,p)) return true;//点在多边形上
        if(fabs(side.s.y-side.e.y)<esp) continue;//平行x轴不做考虑
        if(online(line,side.s))
        {
            if(side.s.y>side.e.y) num++;//此两条语句不能合起来写
        }
        else if(online(line,side.e))
        {
            if(side.e.y>side.s.y) num++;
        }
        else if(intersect(line,side)) num++;
        
    }
    return num&1?2:0;
}

矢量叉积作用-凸多边形排序

对于凸多边形，如果不是按照逆时针顺序排列，可以通过矢量叉积来进行排序、

//多边形点逆时针排序,注意是凸多边形
void adjustThePoint(int n)
{
    vector<Point> p_vector;
    if(n<3) return ;
    p_vector.push_back(p[0]);
    p_vector.push_back(p[1]);
    for(int i=2;i<n;i++)
    {
        int pos=p_vector.size()-1;
        while(pos>0)
        {
            if(multiply(p[0],p[i],p[pos])<0)
            {
                p_vector.insert(p_vector.begin()+pos+1,p[i]);
                break;
            }
            pos--;
        }
        if(!pos) p_vector.insert(p_vector.begin()+1,p[i]);
    }
    int pos=0;
    for(auto &t:p_vector)
        p[pos++]=t;
}