German Collegiate Programming Contest 2018

B:Battle Royale

Battle Royale games are the current trend in video games and Gamers Concealed Punching Circles (GCPC) is the most popular game of them all. The game takes place in an area that, for the sake of simplicity, can be thought of as a two-dimensional plane. Movement and positioning are a substantial part of the gameplay, but getting to a desired location can be dangerous. You are confident in your ability to handle the other players, however, while you are walking to your destination, there are two hazards posed by the game itself:

The game zone is bounded by a blue circle. Outside of this circle, there is a deadly force field that would instantly take you out of the game.
Inside the game zone, there is a red circle where you are exposed to artillery strikes. This circle is also too risky to enter.

You want to move from one spot on the map to another, but the direct path to your destination is blocked by the red circle, so you need to find a way around it. Can you find the shortest path that avoids all hazards by never leaving the blue or entering the red circle? Touching the boundaries of the circles is fine, as long as you do not cross them.

Input Format

The input consists of:

one line with two integers
one line with two integers
one line with three integers
one line with three integers

All coordinates have an absolute value of at most

Output Format

Output the length of the shortest path that does not leave the blue or enter the red circle. The output must be accurate up to a relative or absolute error (whichever is lower) of

本题答案不唯一，符合要求的答案均正确

样例输入

样例输出

10.8112187742
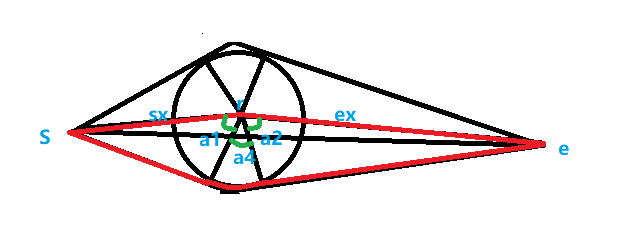
求两点与圆的切线，加一段弧长，如图

#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int main()
{
    double sa,sb,ea,eb,ba,bb,ra,rb,br,rr;
    scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf%lf",&sa,&sb,&ea,&eb,&ba,&bb,&br,&ra,&rb,&rr);
    double sx=sqrt((sa-ra)*(sa-ra)+(sb-rb)*(sb-rb));
    double ex=sqrt((ea-ra)*(ea-ra)+(eb-rb)*(eb-rb));
    double se=sqrt((ea-sa)*(ea-sa)+(eb-sb)*(eb-sb));
    double x1=sqrt((sa-ra)*(sa-ra)+(sb-rb)*(sb-rb)-rr*rr);
    double x2=sqrt((ea-ra)*(ea-ra)+(eb-rb)*(eb-rb)-rr*rr);
    double a1=acos(rr/sx);
    double a2=acos(rr/ex);
    double a3=acos((sx*sx+ex*ex-se*se)/(2*sx*ex));
    double a4=a3-a2-a1;
    double x3=a4*rr;
    printf("%.10lf",x1+x2+x3);
    return 0;
}

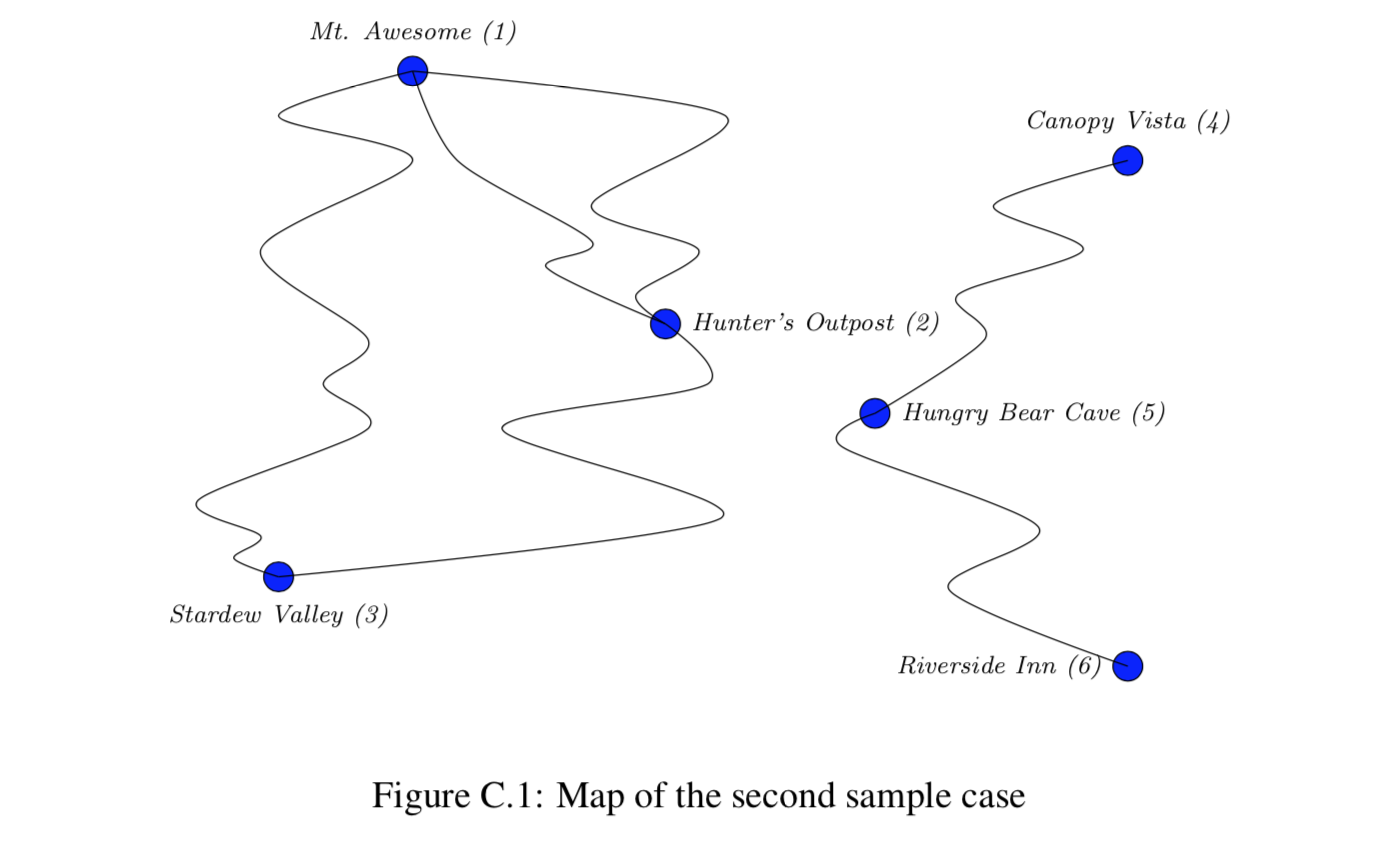
C. Coolest Ski Route

John loves winter. Every skiing season he goes heli-skiing with his friends. To do so, they rent a helicopter that flies them directly to any mountain in the Alps. From there they follow the picturesque slopes through the untouched snow.

Of course they want to ski on only the best snow, in the best weather they can get. For this they use a combined condition measure and for any given day, they rate all the available slopes.

Can you help them find the most awesome route?

Input Format

The input consists of:

one line with two integers

Points without incoming slopes are mountain tops with beautiful scenery, points without outgoing slopes are valleys. The helicopter can land on every connecting point, so the friends can start and end their tour at any point they want. All slopes go downhill, so regardless of where they start, they cannot reach the same point again after taking any of the slopes.

Output Format

Output a single number

Hint

样例输入1

样例输出1

样例输入2

样例输出2

求有向图最长路径

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
vector<pair<int,int> >v[1006];
typedef pair<int,int> p;
int n,m,dis[1006];
void priority_queue_dijkstra()
{
    memset(dis,0,sizeof(dis));
    priority_queue<p,vector<p>,less<p> >q;
    for(int i=1;i<=n;i++)
        q.push(make_pair(0,i));
    while(!q.empty())
    {
        p t=q.top();
        q.pop();
        if(dis[t.second]!=t.first) continue;
        for(int i=0;i<v[t.second].size();i++)
        {
            if(dis[v[t.second][i].first]<t.first+v[t.second][i].second)
            {
                dis[v[t.second][i].first]=t.first+v[t.second][i].second;
                q.push(make_pair(dis[v[t.second][i].first],v[t.second][i].first));
            }
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0,x,y,z;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        v[x].push_back({y,z});
    }
    int inf=-INF;
    priority_queue_dijkstra();
    for(int i=1;i<=n;i++)
        inf=max(inf,dis[i]);
        printf("%d\n",inf);
    return 0;
}

D. Down the Pyramid

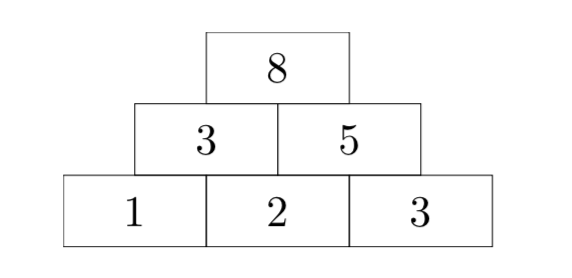
Do you like number pyramids? Given a number sequence that represents the base, you are usually supposed to build the rest of the "pyramid" bottom-up: For each pair of adjacent numbers, you would compute their sum and write it down above them. For example, given the base sequence

However, I am not interested in completing the pyramid – instead, I would much rather go underground. Thus, for a sequence of

Input Format

The input consists of:

one line with the integer
one line with n integers

Output Format

Output a single integer, the number of non-negative integer sequences that would have the input sequence as the next level in a number pyramid.

样例输入1

6
12 5 7 7 8 4

样例输出1

样例输入2

3
10 1000 100

样例输出2

设下一层为x0,x1,x2,x3,x4,xn

则有x0+x1=a[1];x1+x2=a[2],x2+x[3]=a[n],xn-1+xn=a[n];

化简可得n个关于x0的一元不等式，因为x非负，求解可得区间，区间内整数解即为方案数

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int ansl=-INF,ansr=INF;
int n;
int main()
{
    scanf("%d",&n);
    int cnt=0;
    for(int i=1,x;i<=n;i++)
    {
        scanf("%d",&x);
        cnt=cnt*-1+x;
        if(i&1) ansr=min(ansr,cnt);
        else ansl=max(ansl,cnt*-1);
    }
    if(ansr<ansl) printf("0\n");
    else if(ansl<0 && ansr<0) printf("0\n");
    else if(ansl<0 && ansr>=0) printf("%d\n",ansr+1);
    else printf("%d\n",ansr-ansl+1);
    return 0;
}

The heroes of your favorite action TV show are preparing for the final confrontation with the villains. Fundamentally, there are two rivals who will fight each other: a very important main hero who wants to save the universe and an equally important main villain who wants to destroy it. However, through countless recursive spin-offs, they may have slightly less important sidekicks (a hero and a villain who are rivals themselves), who in turn may also have their own (even less important) sidekicks, and so on. Note that there is an equal number of heroes and villains, and each rival pair has at most one sidekick pair.

Initially, every character will fight their rival, with the winner being determined by who has the higher Power Level. If a hero and their corresponding villain have the same Power Level, their battle will be determined by their sidekicks' battle, as the winning sidekick can help as a sort of tiebreaker. (If rivals of equal Power Level do not have sidekicks, the hero character will win with the help of random passersby.) However, whenever a battle is won by either side, there is nothing the sidekicks can do about it – this is because the people behind the show believe some fans might get upset if a character were to get defeated by a bunch of less important characters, so they would lose regardless of the Power Levels.

After the battles between rivals (and possible tiebreakers) are done, the most important character remaining will defeat the rest of the opposing side and determine the fate of the universe. Fortunately, the heroes can ensure victory through hard, rigorous training. For each day they spend training, the Power Level of each hero increases by

But you already knew all this. The question plaguing your mind is how long the training is going to take.

Input Format

The input consists of:

one line with an integer
one line with
one line with

Output Format

Output a single integer, the minimum number of days the heroes need to spend training in order for their side to win.

样例输入1

4
5 3 1 1
8 6 9 1

样例输出1

样例输入2

1
2
1

样例输出2

样例输入3

2
4 2
7 5

样例输出3

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
int n,a[1006],x;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        a[i]=x-a[i];
    }
    int pos=a[1];
    if(pos<0) return 0*printf("0\n");
    for(int i=2;i<=n;i++)
    {
        if(a[i]>pos) return 0*printf("%d\n", pos+1);
        else if(a[i]<pos) return 0*printf("%d\n",pos);
    }
    printf("%d\n",pos);
    return 0;
}

posted @ 2018-07-19 19:34 十年换你一句好久不见阅读(644) 评论(0) 编辑收藏举报

刷新页面返回顶部

十年换你一句好久不见

German Collegiate Programming Contest 2018​

B:Battle Royale

Input Format

Output Format

样例输入

样例输出

C. Coolest Ski Route

Input Format

Output Format

Hint

样例输入1

样例输出1

样例输入2

样例输出2

D. Down the Pyramid

Input Format

Output Format

样例输入1

样例输出1

样例输入2

样例输出2

Input Format

Output Format

样例输入1

样例输出1

样例输入2

样例输出2

样例输入3

样例输出3

公告

German Collegiate Programming Contest 2018