划分树

　　划分树是基于线段树的一种数据结构，主要用于快速求出(log(n)时间的时间复杂度内))序列区间的第K大值

      划分树主要分为两部分，建树和查询。

建树：

　　建树是模拟了快速排序和快速排序，所建的树每一层都有n个元素，但是根据根节点将子层分为左右子节点，但保证的是，左子节点内的所有元素严格不大于右子节点内的所有元素。说到这里，建树的核心已经很清楚了，每次要递归的区间，找到其中位数，小于中位数的放到左子节点内，大于中位数的放到右子节点。同时这样会保证，在同一个节点内，元素的相对位置相比于原序列来说，相对位置没有发生变化。但是在分配元素的过程中还存在着一个问题，那就是中位数在需要处理的区间内，可能不止一个，这种情况就要单独分配，以为，根节点所管辖的区间一旦确立，在左右子节点内元素的个数是确定的，所有将中位数按位补充分配到左右字节点内（看代码实现）。之后不断递归建树就可以了。直到处理区间左右边界相等，递归终止。可能这样说不太容易理解。直接上图。

 

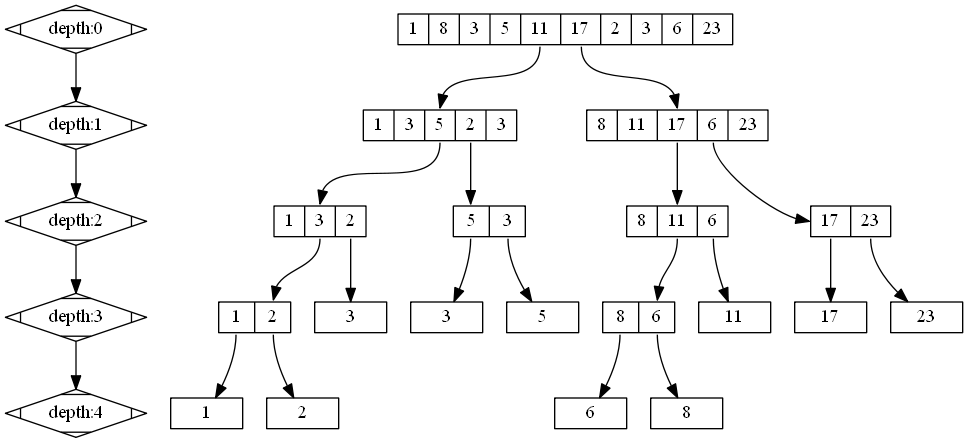
　　建树过程中有十分重要的一部分，就是相对于树的每层都有一个标记数组toleft，标记的是当前节点之前包括当前节点被分配到左子树中的元素的个数

以第0层为例：

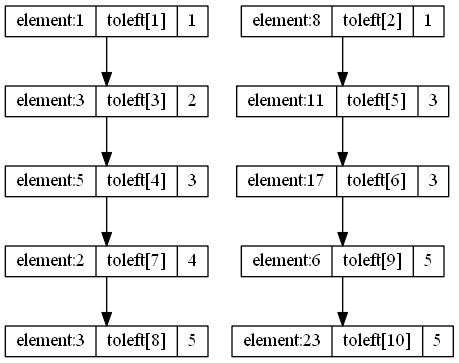
假设区间为[l,r],则区间内被分配到左子树的元素个数为toleft[r]-toleft[l-1],则被分配到右子树的个数就为r-l+1-toleft[r]+toleft[l-1];

代码实现建树

 

const int maxn=100010;
int tree[20][maxn];//1000000个元素最多20层
int sorted[maxn];//初始排序，便于快速查找区间中位数
int toleft[20][maxn];//标记数组
int n,m;
void build(int l,int r,int dep)
{
    if(l==r) return ;
    int mid=l+r>>1;
    int same=mid-l+1;
    for(int i=l;i<=r;i++)
        if(tree[dep][i]<sorted[mid]) same--;//单独处理中位数，看小于中位数的分配完后，左子树是否有多余的空位
    int lpos=l,rpos=mid+1;
    for(int i=l;i<=r;i++)
    {
        if(tree[dep][i]<sorted[mid]) tree[dep+1][lpos++]=tree[dep][i];
        else if(tree[dep][i]==sorted[mid] && same) tree[dep+1][lpos++]=tree[dep][i],same--;
        else tree[dep+1][rpos++]=tree[dep][i];
        toleft[dep][i]=toleft[dep][l-1]+lpos-l;//标记被分配到左子树的个数
    }
    build(l,mid,dep+1);
    build(mid+1,r,dep+1);
}

 

查询：

 查询是在每一层的toleft的基础上进行区间的缩小，直到待查询区间缩小为1即为查询结果

总区间为[L,R],待查区间为[l,r];k是第K大值，toleft[r]-toleft[l-1]为区间[l,r]内被分配到左子数的个数.

toleft[r]-toleft[l-1]>=k

说明第k大值一定在左子树此时就可以更新区间，首先大区间二分为[L,L+R>>1],然后考虑小区间，可以确定的是，[l,r]分配在左子树的元素一定在区间[L,L+R>>1]内，所以，确定左边界sl=L+toleft[l-1]-toleft[L-1]:toleft[l-1]-toleft[L-1]为[L,l-1]内被分配到左子树的个数，他们不在查找之列，但相对位置不变，这些元素一定排在前面，以此来确定左边界，右边界就好确定了，因为toleft[r]-toleft[l-1]>=k，所以左边界加上toleft[r]-toleft[l-1]-1即可，即sr=sl+toleft[r]-toleft[l-1]-1,同时必有L<=sl,sr<=L+R>>1;

 toleft[r]-toleft[l-1]<k

此时，元素在右子树，二分大区间[L+R>>1|1,R],确定右边界，sr=r+toleft[R]-toleft[r],因为相对位置不变，toleft[R]-toleft[r]是分配在左子树的必定会往前移动，所以右边界往后移动，右边界确定后，确定左边界sl=sr-(l-r-toleft[l-1]-toleft[L-1]),减去分配到左子树的，剩下就在右子树。注意，此时要更新k k=k--toleft[l-1]-toleft[L-1]，已经确定前面有toleft[l-1]-toleft[L-1]比其小，所以就是求右子树内区间[sl,sr]第k--toleft[l-1]-toleft[L-1]小。

具体实现看代码

 

int query(int L,int R,int l,int r,int dep,int k)
{
    if(l==r) return tree[dep][l]; 
    int mid=L+R>>1;
    int cnt=toleft[dep][r]-toleft[dep][l-1];
    if(cnt>=k)
    {
        int newl=L+toleft[dep][l-1]-toleft[dep][L-1];
        int newr=newl+cnt-1;
        return query(L,mid,newl,newr,dep+1,k);
    }
    else 
    {
        int newr=r+toleft[dep][R]-toleft[dep][r];
        int newl=newr-(r-l-cnt);
        return query(mid+1,R,newl,newr,dep+1,k-cnt);
    }
}