coedforces #481Div（3）（ABCDEFG）

A. Remove Duplicates

Petya has an array $a$consisting of $n$integers. He wants to remove duplicate (equal) elements.Petya wants to leave only the rightmost entry (occurrence) for each element of the array. The relative order of the remaining unique elements should not be changed.

Input

The first line contains a single integer $n$$\mathrm{(1\le n\le 50}$) — the number of elements in Petya's array.

The following line contains a sequence ${\mathrm{a1,a2,\dots ,an}}^{}$$\mathrm{(1\le ai\le 1000}$) — the Petya's array.

Output

In the first line print integer $x$— the number of elements which will be left in Petya's array after he removed the duplicates.In the second line print $x$

$\mathrm{integers\; separated\; with\; a\; space\; —\; Petya\text{'}s\; array\; after\; he\; removed\; the\; duplicates.\; For\; each\; unique\; element\; only\; the\; rightmost\; entry\; should\; be\; left.}$

 

Examples

Input

6
1 5 5 1 6 1

Output

3
5 6 1 

Input

5
2 4 2 4 4

Output

2
2 4 

Input

5
6 6 6 6 6

Output

1
6 Note

In the first example you should remove two integers $1$$\mathrm{,\; which\; are\; in\; the\; positions\; 1\; and\; 4.\; Also\; you\; should\; remove\; the\; integer\; 5,\; which\; is\; in\; the\; position\; 2}$.

In the second example you should remove integer $2$$\mathrm{,\; which\; is\; in\; the\; position\; 1,\; and\; two\; integers\; 4,\; which\; are\; in\; the\; positions\; 2\; and\; 4}$.

In the third example you should remove four integers $6$$\mathrm{,\; which\; are\; in\; the\; positions\; 1,\; 2,\; 3\; and\; 4.}$

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
int n,a[56][2];
set<int>s;
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i][0]);
    int ans=0;
    for(int i=n-1;i>=0;i--)
    {
        if(s.count(a[i][0])) a[i][1]=1;
        else a[i][1]=0,ans++;
        s.insert(a[i][0]);
    }
    printf("%d\n",ans);
    for(int i=0;i<n;i++)
    {
        if(!a[i][1]) printf("%d ",a[i][0]);
    }
    return 0;
}

 

B. File Name

 

You can not just take the file and send it. When Polycarp trying to send a file in the social network "Codehorses", he encountered an unexpected problem. If the name of the file contains three or more "x" (lowercase Latin letters "x") in a row,

the system considers that the file content does not correspond to the social network topic. In this case, the file is not sent and an error message is displayed.

Determine the minimum number of characters to remove from the file name so after that the name does not contain "xxx" as a substring. Print 0 if the file name does not initially contain a forbidden substring "xxx".

You can delete characters in arbitrary positions (not necessarily consecutive). If you delete a character, then the length of a string is reduced by $1$$\mathrm{.\; For\; example,\; if\; you\; delete\; the\; character\; in\; the\; position\; 2}$from the string "exxxii", then the resulting string is "exxii".

 

Input

The first line contains integer $n$$\mathrm{(3\le n\le 100)}$— the length of the file name.

 

The second line contains a string of length $n$

 

consisting of lowercase Latin letters only — the file name.

 

Output

Print the minimum number of characters to remove from the file name so after that the name does not contain "xxx" as a substring.

If initially the file name dost not contain a forbidden substring "xxx", print 0.

 

Examples

Input

6
xxxiii

Output

1

Input

5
xxoxx

Output

0

Input

10
xxxxxxxxxx

Output

8

 

Note

In the first example Polycarp tried to send a file with name contains number $33$$\mathrm{,\; written\; in\; Roman\; numerals.}$

$\mathrm{But\; he\; can\; not\; just\; send\; the\; file,\; because\; it\; name\; contains\; three\; letters\; "x"\; in\; a\; row.\; To\; send\; the\; file\; he\; needs\; to\; remove\; any\; one\; of\; this\; letters.}$

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
char a[106];
int n;
int main()
{
    scanf("%d",&n);
    scanf("%s",a);
    int ans=0,pos=0;
    for(int i=0;i<n;i++)
    {
        if(a[i]=='x') ans++;
        else
        {
            if(ans>=3) pos+=ans-2;
            ans=0;
        }
    }
    if(ans>=3) pos+=ans-2;
    printf("%d\n",pos);
    return 0;
}

C. Letters

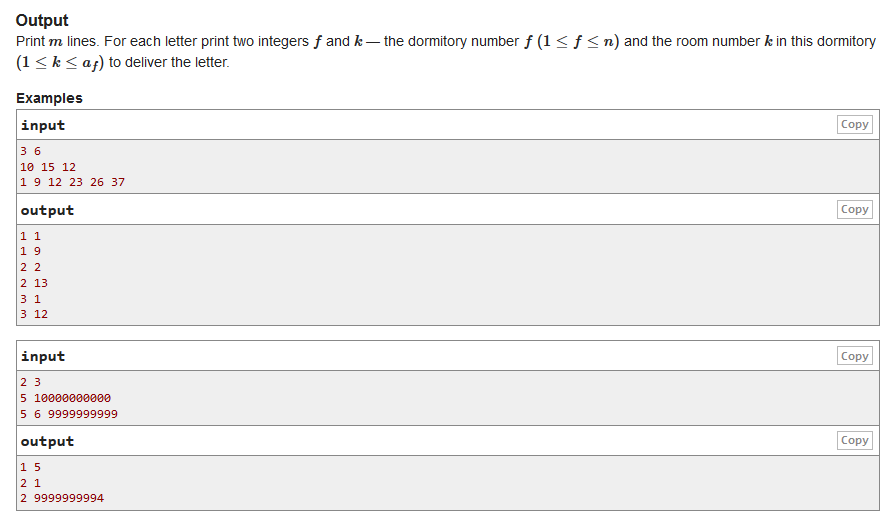
前缀和+二分

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
ll a[200005],x,n,m,q;
int main()
{
    scanf("%lld%lld",&n,&m);
    a[0]=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&x);
        a[i]=a[i-1]+x;
    }
    while(m--)
    {
        scanf("%lld",&q);
        ll k=lower_bound(a+1,a+n+1,q)-a;
        printf("%lld %lld\n",k,q-a[k-1]);
    }
    return 0;
}

 

D. Almost Arithmetic Progression

Polycarp likes arithmetic progressions. A sequence $[a1,a2,\dots ,an]$

is called an arithmetic progression if for each $\mathrm{i\; (1\le i<n)\; the\; value\; ai+1-ai\; is\; the\; same.\; For\; example,\; the\; sequences\; [42],\; [5,5,5],\; [2,11,20,29]\; and\; [3,2,1,0]\; are\; arithmetic\; progressions,\; but\; [1,0,1],\; [1,3,9]\; and\; [2,3,1]}$

are not.It follows from the definition that any sequence of length one or two is an arithmetic progression.Polycarp found some sequence of positive integers $[b1,b2,\dots ,bn]$

$\mathrm{.\; He\; agrees\; to\; change\; each\; element\; by\; at\; most\; one.\; In\; the\; other\; words,\; for\; each\; element\; there\; are\; exactly\; three\; options:\; an\; element\; can\; be\; decreased\; by\; 1,\; an\; element\; can}$

$\mathrm{beincreased\; by\; 1}$, an element can be left unchanged.Determine a minimum possible number of elements in $b$$\mathrm{which\; can\; be\; changed\; (by\; exactly\; one),\; so\; that\; the\; sequence\; b}$

becomes an arithmetic progression, or report that it is impossible.It is possible that the resulting sequence contains element equals $0$.

Input

The first line contains a single integer $n$$\mathrm{(1\le n\le 100000)\; —\; the\; number\; of\; elements\; in\; b}$.

The second line contains a sequence ${\mathrm{b1,b2,\dots ,bn}}^{}$$\mathrm{(1\le bi\le 109)}$

.

Output

If it is impossible to make an arithmetic progression with described operations, print -1. In the other case, print non-negative integer — the minimum number of elements to change to make the given equence becomes an arithmetic progression. The only allowed operation is to add/to subtract one from an element (can't use operation twice tothesameposition).

Examples

Input

Copy

4
24 21 14 10

Output

Copy

3

Input

Copy

2
500 500

Output

Copy

0

Input

Copy

3
14 5 1

Output

Copy

-1

Input

Copy

5
1 3 6 9 12

Output

Copy

1

Note

In the first example Polycarp should increase the first number on $1$$\mathrm{,\; decrease\; the\; second\; number\; on\; 1,\; increase\; the\; third\; number\; on\; 1,\; and\; the\; fourth\; number\; should\; left}$

$\mathrm{unchanged.\; So,\; after\; Polycarp\; changed\; three\; elements\; by\; one,\; his\; sequence\; became\; equals\; to\; [25,20,15,10]}$, which is an arithmetic progression.

In the second example Polycarp should not change anything, because his sequence is an arithmetic progression.

In the third example it is impossible to make an arithmetic progression.In the fourth example Polycarp should change only the first element, he should decrease it on one.

After that his sequence will looks like $[0,3,6,9,12]$, which is an arithmetic progression.

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
int dir[10][2]={{1,0},{-1,0},{-1,1},{0,1},{1,-1},{0,-1},{0,0},{1,1},{-1,-1}};
int n,ans=INF,a[100005],b[100005],pos,cnt,flag;
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
    if(n<=2) return printf("0\n"),0;
    for(int i=0;i<9;i++)
    {
        pos=0;flag=0;
        if(dir[i][0]!=0) pos++;
        if(dir[i][1]!=0) pos++;
        b[0]=a[0]+dir[i][0];
        b[1]=a[1]+dir[i][1];
        cnt=b[1]-b[0];
        for(int j=2;j<n;j++)
        {
            if(a[j]+1-b[j-1]==cnt) b[j]=a[j]+1,pos++;
            else if(a[j]-b[j-1]==cnt) b[j]=a[j];
            else if(a[j]-1-b[j-1]==cnt) b[j]=a[j]-1,pos++;
            else
            {
                flag=1;
                break;
            }
        }
        if(!flag) ans=min(ans,pos);
    }
    if(ans==INF) printf("-1\n");
    else printf("%d\n",ans);
    return 0;
}

E. Bus Video System

The busses in Berland are equipped with a video surveillance system. The system records information about changes in the number of passengers in a bus after stops.If $x$

is the number of passengers in a bus just before the current bus stop and $\mathrm{y\; is\; the\; number\; of\; passengers\; in\; the\; bus\; just\; after\; current\; bus\; stop,\; the\; system\; records\; the}$

$\mathrm{numbery-x}$. So the system records show how number of passengers changed.The test run was made for single bus and $n$$\mathrm{bus\; stops.\; Thus,\; the\; system\; recorded\; the\; sequence\; of\; integers\; a1,a2,\dots ,an\; (exactly\; one\; number\; for\; each\; bus\; stop),\; where\; ai\; is\; the\; record\; for\; the\; bus\; stop\; i.\; The\; bus\; stops\; are\; numbered\; from\; 1\; to\; n}$

in chronological order.

Determine the number of possible ways how many people could be in the bus before the first bus stop, if the bus has a capacity equals

to $w$$\mathrm{(that\; is,\; at\; any\; time\; in\; the\; bus\; thereshould\; be\; from\; 0\; to\; w}$passengers inclusive).

Input

The first line contains two integers $n$$\mathrm{and\; w\; (1\le n\le 1000,1\le w\le 109)}$— the number of bus stops and the capacity of the bus.

The second line contains a sequence ${\mathrm{a1,a2,\dots ,an}}^{}$

$\mathrm{(-106\le ai\le 106),\; where\; ai\; equals\; to\; the\; number,\; which\; has\; been\; recorded\; by\; the\; video\; system\; after\; the\; i}$-th bus stop.

Output

Print the number of possible ways how many people could be in the bus before the first bus stop, if the bus has a capacity equals to $w$. If the situation is contradictory (i.e. for any initial number of passengers there will be a contradiction), print 0.

Examples

Input

Copy

3 5
2 1 -3

Output

Copy

3

Input

Copy

2 4
-1 1

Output

Copy

4

Input

Copy

4 10
2 4 1 2

Output

Copy

2

Note

In the first example initially in the bus could be $0$$\mathrm{,\; 1\; or\; 2}$passengers.

In the second example initially in the bus could be $1$$\mathrm{,\; 2,\; 3\; or\; 4}$passengers.

In the third example initially in the bus could be $0$$\mathrm{or\; 1}$passenger.

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
const int N = 1010;
ll n, w, a[N];
int main() {
    cin >> n >> w >> a[0];
    for(int i = 1; i < n; i ++) {
        cin >> a[i];
        a[i] += a[i-1];
    }
    ll MIN = 1e12, MAX = -1e12;
    for(int i = 0; i < n; i ++) {
        MIN = min(MIN, a[i]);
        MAX = max(MAX, a[i]);
    }
    if(MIN < 0 && MAX < 0) {
        cout << max(0,w + MIN+1) << endl;
    } else if(MAX >= 0 && MIN < 0) {
        MAX -= MIN;
        cout << max(0,w - MAX + 1) << endl;
    } else if(MAX >= 0 && MIN >= 0) {
        cout << max(0, w - MAX + 1) << endl;
    }
    return 0;
}

F. Mentors

 

In BerSoft $n$programmers work, the programmer $\mathrm{i\; is\; characterized\; by\; a\; skill\; ri}$.A programmer $a$$\mathrm{can\; be\; a\; mentor\; of\; a\; programmer\; b\; if\; and\; only\; if\; the\; skill\; of\; the\; programmer\; a\; isstrictly\; greater\; thanthe\; skill\; of\; the\; programmer\; b\; (ra>rb)\; and\; programmers\; a\; and\; b}$

are not in a quarrel.You are given the skills of each programmers and a list of $k$$\mathrm{pairs\; of\; the\; programmers,\; which\; are\; in\; a\; quarrel\; (pairs\; are\; unordered).\; For\; each\; programmer\; i,\; find\; the\; number\; of\; programmers,\; for\; which\; the\; programmer\; i}$can be a mentor.

Input

The first line contains two integers $n$$\mathrm{and\; k\; (2\le n\le 2\cdot 105,\; 0\le k\le min(2\cdot 105,n\cdot (n-1)2))}$— total number of programmers and number of pairs of programmers which are in a quarrel.The second line contains a sequence of integers ${\mathrm{r1,r2,\dots ,rn}}^{}$$\mathrm{(1\le ri\le 109),\; where\; ri\; equals\; to\; the\; skill\; of\; the\; i}$

-th programmer.

Each of the following $k$

$\mathrm{lines\; contains\; two\; distinct\; integers\; x,\; y\; (1\le x,y\le n,\; x\ne y)\; —\; pair\; of\; programmers\; in\; a\; quarrel.\; The\; pairs\; are\; unordered,\; it\; means\; that\; if\; x\; is\; in\; a\; quarrel\; with\; y\; then\; y\; is\; in\; a\; quarrel\; with\; x.\; Guaranteed,\; that\; for\; each\; pair\; (x,y)\; there\; are\; no\; other\; pairs\; (x,y)\; and\; (y,x)}$in the input.

Output

Print $n$$\mathrm{integers,\; the\; i-th\; number\; should\; be\; equal\; to\; the\; number\; of\; programmers,\; for\; which\; the\; i}$-th programmer can be a mentor. Programmers are numbered in the same order that their skills are given in the input.

Examples

Input

Copy

4 2
10 4 10 15
1 2
4 3

Output

Copy

0 0 1 2 

Input

Copy

10 4
5 4 1 5 4 3 7 1 2 5
4 6
2 1
10 8
3 5

Output

Copy

5 4 0 5 3 3 9 0 2 5 

Note

In the first example, the first programmer can not be mentor of any other (because only the second programmer has a skill, lower than first programmer skill, but they are in a quarrel). The second programmer can not be mentor of any other programmer, because his skill is minimal among others. The third programmer can be a mentor of the second programmer. The fourth programmer can be a mentor of the first and of the second programmers. He can not be a mentor of the third programmer, because they are in a quarrel.

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
int n,k,a[200006],b[200006];
vector<int>v[200005];
int main()
{
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
        b[i]=a[i];
    }
    for(int i=0,x,y;i<k;i++)
    {
        scanf("%d%d",&x,&y);
        v[x-1].push_back(y-1);
        v[y-1].push_back(x-1);
    }
    sort(b,b+n);
    for(int i=0;i<n;i++)
    {
        int ans=lower_bound(b,b+n,a[i])-b;
        for(int j=0;j<v[i].size();j++)
            if(a[v[i][j]]<a[i]) ans--;
        printf("%d ",ans);
    }
    return 0;
}

G. Petya's Exams

Petya studies at university. The current academic year finishes with $n$special days. Petya needs to pass $\mathrm{m\; exams\; in\; those\; special\; days.\; The\; special\; days\; in\; this\; problem\; arenumbered\; from\; 1\; to\; n}$

.There are three values about each exam:

• ${\mathrm{si}}^{}$$\mathrm{—\; the\; day,\; when\; questions\; for\; the\; i}$-th exam will be published,

• ${\mathrm{di}}^{}$$\mathrm{—\; the\; day\; of\; the\; i-th\; exam\; (si<di}$),

• ${\mathrm{ci}}^{}$$\mathrm{—\; number\; of\; days\; Petya\; needs\; to\; prepare\; for\; the\; i-th\; exam.\; For\; the\; i-th\; exam\; Petya\; should\; prepare\; in\; days\; between\; si\; and\; di-1}$, inclusive.

There are three types of activities for Petya in each day: to spend a day doing nothing (taking a rest), to spend a day passing exactly one exam or to spend a day preparing for exactly one exam. So he can't pass/prepare for multiple exams in a day. He can't mix his activities in a day. If he is preparing for the $i$

$\mathrm{th\; exam\; in\; day\; j,\; then\; si\le j<di}$.

It is allowed to have breaks in a preparation to an exam and to alternate preparations for different exams in consecutive days. So preparation for an exam is not required to be done in consecutive days.

Find the schedule for Petya to prepare for all exams and pass them, or report that it is impossible.

Input

The first line contains two integers $n$$\mathrm{and\; m\; (2\le n\le 100,1\le m\le n)}$— the number of days and the number of exams.Each of the following $m$

$\mathrm{lines\; contains\; three\; integers\; si,\; di,\; ci\; (1\le si<di\le n,1\le ci\le n)\; —\; the\; day,\; when\; questions\; for\; the\; i-th\; exam\; will\; be\; given,\; the\; day\; of\; the\; i-th\; exam,\; number\; of\; days\; Petya\; needs\; to\; prepare\; for\; the\; i}$-th exam.

Guaranteed, that all the exams will be in different days. Questions for different exams can be given in the same day. It is possible that, in the day of some exam, the questions for other exams are given.

Output

If Petya can not prepare and pass all the exams, print -1. In case of positive answer, print $n$$\mathrm{integers,\; where\; the\; j}$-th number is:$(m+1)$$\mathrm{,\; if\; the\; j}$-th day is a day

of some exam (recall that in each day no more than one exam is conducted),zero, if in the $j$-th day Petya will have a rest,$i$$\mathrm{(1\le i\le m),\; if\; Petya\; will\; prepare\; for\; the\; i-th\; exam\; in\; the\; day\; j\; (the\; total\; number\; of\; days\; Petya\; prepares\; for\; each\; exam\; should\; be\; strictly\; equal\; to\; the\; number\; of\; days\; needed\; to\; prepare\; for\; it).}$

Assume that the exams are numbered in order of appearing in the input, starting from $1$If there are multiple schedules, print any of them.

Examples

Input

Copy

5 2
1 3 1
1 5 1

Output

Copy

1 2 3 0 3 

Input

Copy

3 2
1 3 1
1 2 1

Output

Copy

-1

Input

Copy

10 3
4 7 2
1 10 3
8 9 1

Output

Copy

2 2 2 1 1 0 4 3 4 4 

Note

In the first example Petya can, for example, prepare for exam $1$$\mathrm{in\; the\; first\; day,\; prepare\; for\; exam\; 2\; in\; the\; second\; day,\; pass\; exam\; 1\; in\; the\; third\; day,\; relax\; in\; the\; fourth\; day,\; and\; pass\; exam\; 2}$in the fifth day. So, he can prepare and pass all exams.In the second example, there are three days and two exams. So, Petya can prepare in only one day (because in two other days he should pass exams). Then Petya can not prepare and pass all exams.

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
struct node
{
    int s,d,c;
    bool operator<(const node &a)const
    {
        return a.s==s?a.d>d:a.s>s;
    }
}e[106];
int a[106];
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    memset(a,0,sizeof(-1));
    for(int i=0;i<m;i++)
    {
        scanf("%d%d%d",&e[i].s,&e[i].d,&e[i].c);
        a[e[i].d]=m+1;
    }
    int top;
    int flag=0;
    for(int i=0;i<m;i++)
    {
        top=e[i].s;
        while(top<e[i].d && top<=n && e[i].c>0)
        {
            if(!a[top])
            {
                a[top]=i+1;
                e[i].c--;
            }
            top++;
        }
        if(e[i].c>0) flag=1;
    }
    if(flag) printf("-1\n");
    else
    {
        for(int i=1;i<=n;i++)
            printf("%d ",a[i]);
    }
    return 0;
}