963B：Destruction of a Tree

You are given a tree (a graph with n vertices and n - 1 edges in which it's possible to reach any vertex from any other vertex using only its edges).

A vertex can be destroyed if this vertex has even degree. If you destroy a vertex, all edges connected to it are also deleted.

Destroy all vertices in the given tree or determine that it is impossible.

Input

The first line contains integer n (1 ≤ n ≤ 2·10⁵) — number of vertices in a tree.

The second line contains n integers p₁, p₂, ..., p_n (0 ≤ p_i ≤ n). If p_i ≠ 0 there is an edge between vertices i and p_i. It is guaranteed that the given graph is a tree.

Output

If it's possible to destroy all vertices, print "YES" (without quotes), otherwise print "NO" (without quotes).

If it's possible to destroy all vertices, in the next n lines print the indices of the vertices in order you destroy them. If there are multiple correct answers, print any.

Examples

Input

Copy

5
0 1 2 1 2

Output

Copy

YES
1
2
3
5
4

Input

Copy

4
0 1 2 3

Output

Copy

NO

Note

In the first example at first you have to remove the vertex with index 1 (after that, the edges (1, 2) and (1, 4) are removed), then the vertex with index 2 (and edges (2, 3) and (2, 5) are removed). After that there are no edges in the tree, so you can remove remaining vertices in any order.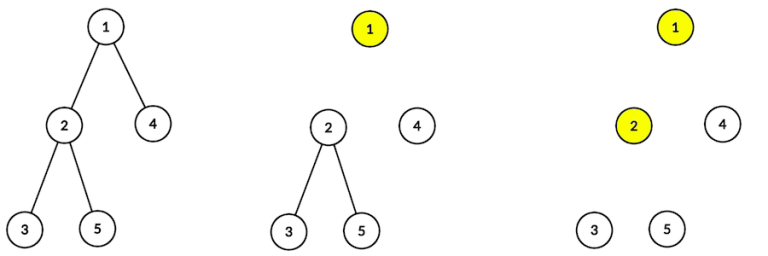

规定一个顺序，使分为父子结点，则每次删除只能往子节点查找

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
#define ll long long
vector<int>v[200005],ans;
stack<int>q;
int cnt[200005],vis[200005];
int n,x,pos,par[200005];
void bfs(int now)
{
    ans.push_back(now);
    vis[now]=1;
    for(int i=0;i<v[now].size();i++)
    {
        cnt[v[now][i]]--;
        if(v[now][i]==par[now] || vis[v[now][i]]) continue;//当前节点已经被找过，或者是now节点的父节点
        if(!(cnt[v[now][i]]&1)) bfs(v[now][i]);
    }
}
void dfs(int fa,int now)
{
    par[now]=fa;
    q.push(now);
    for(int i=0;i<v[now].size();i++)
    {
        if(v[now][i]==fa) continue;
        dfs(now,v[now][i]);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        if(x)
        {
            v[i].push_back(x);
            v[x].push_back(i);
            cnt[i]++;
            cnt[x]++;
        }
        else pos=i;
    }
    dfs(0,pos);//n-1条边，则必有一个为0，不妨把这点作为根节点遍历。
    memset(vis,0,sizeof(vis));
    while(!q.empty())
    {
        int fr=q.top();
        q.pop();
        if(!(cnt[fr]&1)) bfs(fr);//从后向前遍历，若存在，必只有一个结点符合初始为偶数
    }
    if(ans.size()==n)
    {
        printf("YES\n");
        for(int i=0;i<ans.size();i++)
            printf("%d\n",ans[i]);
    }
    else printf("NO\n");
    return 0;
}