编译器是如何实现32位整型的常量整数除法优化的?[C/C++]
引子
在我之前的一篇文章[ ThoughtWorks代码挑战——FizzBuzzWhizz游戏 通用高速版(C/C++ & C#) ]里曾经提到过编译器在处理除数为常数的除法时,是有优化的,今天整理出来,一来可以了解是怎么实现的,二来如果你哪天要写编译器,这个理论可以用得上。此外,也算我的一个笔记。

实例
我们先来看一看编译器优化的实例。我们所说的除数为常数的整数除法(针对无符号整型, 有符号整型我们后面再讨论),指的是,对于unsigned int a, b, c,例如:a / 10, b / 5, c / 3 诸如此类的整数除法,我们先来看看编译器 unsigned int a, p; p = a / 10; 是如何实现的,下图是 VS 2013 优化的结果,反汇编结果如下:

测试代码如下:
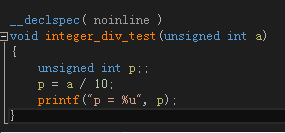
我们可以看到,编译器并没有编译成整数除法DIV指令,而是先乘以一个0xCCCCCCCD(MUL指令),再把EDX右移了3位(SHR edx, 0x03),EDX的值就是我们要求的商。
其原理整理后即为:Value / 10 ~= [ [ (Value * 0xCCCCCCCD) / 2^32 ] / 2^3 ],方括号代表取整。
首先我们要知道一个东西,就是,Intel x86上32位无符号整型(uint32_t)相乘的结果其实是一个64位的整型,即uint64_t,相乘的结果保存在 EAX 和 EDX 两个寄存器里,EAX, EDX都是32位的,合在一起便是一个64位的整数了,一般记为 EDX : EAX,其中EAX是uint64_t的低位,EDX是高位。这个特性在大多数32位的CPU上都存在,即整数乘法结果的位长是被乘数位长的两倍,当然也不排除部分CPU因为某些特殊原因,其相乘的结果依然和被乘数的位长一样,但这样的CPU应该很少见。只有满足这个特性的CPU,常量的整数除法优化才能得以实现。

至于为什么不直接使用DIV指令,原因是:即使在当今发展已经比较完善也比较流行的x86系列CPU上,整数或浮点的除法指令依然是一条比较慢的指令,CPU在整数或浮点除法一般有两种实现方法,一种是试商法(这个非常类似人类在计算除法的过程,只不过这里CPU使用的是二进制来试商,用条件判断来判断如何结束),另一种是乘以 除数 的倒数(即 x (1.0 / 除数)),把除法变为乘法,因为乘法在CPU里实现是比较容易的,只需实现位移和加法器即可,并且可以并行处理。前一种方法,跟人类计算除法类似,无法做到并行处理,且计算过程是不定长的,可能很快就结束(刚好整除),可能要计算到合适的精度为止。而第二种方法,因为用无穷级数求(1.0 / 除数)的过程涉及精度问题,这个过程花的时间也是不定长的,而且用这种方法的时候,必须把整数除法转换为浮点除法才能进行,最后把结果再转换为整型。而试商法可以把整除除法和浮点除法分为两套方案,也可以合为一套方案。至于效率,第二种方法较快,但耗电会比第一种方法大,因为要用到大量的乘法器,所以x86上具体用的是那一种方法,我也不是很清楚,但是Intel手册上写着,Core 2架构的DIV指令的执行周期大概是13-84个周期不等。后续出的新CPU除法指令有没有更快我不太清楚,从实现原理上,终究是没有乘法快的,除非除法的设计有大的突破,因为Core 2上整数/浮点乘法就只需要3个时钟周期,想接近乘法的效率是很难的,关键的一点就是,目前,除法指令的时钟周期是变长的,可能很短,可能很长,平均花费的时钟周期是乘法指令的N倍。
原理
那么,这么优化的原理是什么?怎么得到的?可以应用于所有除数是uint32_t的常量的整数除法吗?答案是:可以的。但前提条件是,除数必须是常量,如果是变量,编译器也只能老老实实使用DIV指令。
由于博客园对LeTex支持不够好(不方便,颜色也不好看),所以我把推演的过程放到了 [这个网站] ,下面是推演过程的截图:
(由于 $c = 2^k$ 的时候,我们可以直接使用位移来实现除法,所以这种情况我们不做讨论。)

上图是原理的推演过程,下面我们来分析一下误差:

其实,如果向上取整不满足(1)式,那么向下取整必然满足(1)式,为什么呢?
虽然向上取整的结果是大于真实值的,向下取整的结果是小于真实值的,不管是大于还是小于,我们都称之为误差,向下取整的误差分析跟上面的类似。
我们设向上取整的误差为 $e$,向下取整的误差为 $e'$,则必有:$e + e' = 1$,(因为如果向上取整的误差为0.2,那么向下取整的误差必然是0.8)
而如果 $0 <= e < 2^k / c$ 不满足,意味着必然满足: $0 <= (1 - e) < 2^k / c$,(这里 $c$ 是满足 $2^k < c < 2^(k+1)$ 的,所以 $0.5 < 2^k / c < 1$ )
即有:$0 <= e' < 2^k / c$ ,就是说如果 $e$ 不满足(1)式,则 $e'$ 必然满足(1)式。
即使最极端的情况下,$e = 0.5$ 的时候,因为 $0.5 < 2^k / c < 1$,所以 $e = e' = 0.5$ 必然是满足(1)式的。
结论

实践
知道了原理,那么我们来实际演算一下 /10 的优化,除数 c = 10, 优先找一个数 k,满足 2^k < c < 2^(k+1),那么 k 为 3,因为 2^3 < 10 < 2^(3+1),我们设要求的相乘的系数为 m, 那么另 m = [2^(32+k) / c],这里用向上取整,即 m = [2^(32+3) / 10] = [3435973836.8] = 3435973837,即十六进制表示法的 0xCCCCCCCD,最大误差为 e = 0.2 (因为我们放大了(3435973837 -3435973836.8) = 0.2),我们看是否满足(1)式,代入:0 < 0.2 < 2^3 / 10,即 0 < 0.2 < 0.8,成立,所以相乘系数 0xCCCCCCCD 是成立的,且向右位移的位数为 k = 3 位,跟文章前面所演示的一致。
我们再看看编译器对其他 c 值的优化系数,我们可以得知 /100 的相乘系数为:0x51EB851F, 右移5位,/3 的相乘系数为:0xAAAAAAAB, 右移1位,/5 的相乘系数为:0xCCCCCCCD, 右移2位,其实它就等价于 /10,只是位移少1位,或者说 /10 其实是等价于 /5 的,只是位移量不同而已。/1000 的相乘系数为:0x10624DD3, 右移6位,/125 的相乘系数为:0x10624DD3, 右移3位。
我们发现,其实对于除数 c ,如果 c 能够被 $2^N$ 整除,可以先把 $c$ 化为 $c = 2^N * c'$,再对 c' 做上面的优化处理,然后再在右移的位数再加上 N 位右移即可,不过其实不做这一步也是可以的,但是这样做有利于缩小相乘系数的范围。
32位有符号整型的优化
非常类似于32位无符号整型的除法优化,依然以 / 10 为例,优化的结果为:

我们可以看到,优化的过程为,乘以一个32位整型 0x66666667,(高位)算术右位移 2 位,再把高位逻辑右移31位(实际是取得高位的符号位),再在原EDX的基础上再加上这个值(这个值当被除数为负数时为1,被除数为正数时为0)。当被除数 a 为正数时,我们很容易理解,推理也如同上面的32位无符号整型一模一样,0x66666667 这个数的取值是由32位有符号整型的正数范围是 0 ~ 2^31-1 决定的,推演过程类似32位无符号整型。
当被除数 a 为负数时,情况略微复杂。首先,我们来看看整数取整是怎么定义的,当 a >= 0 时, | a | 为小于或等于 a 的最小整数,当 a < 0 时, | a | 为大于或等于 a 的最小整数。那么对于负数,例如:|-0.5| = 大于或等于-0.5的最小整数,即 |-0.5| = 0,依此可得:|-1.5| = -1.0,|-11.3| = -11.0。
我们再以 /10 为例,如果 $a = -5$,则 $a / 10 = -5 / 10 = q + r = (-1.0) + 0.5$,而$|a / 10| = |-5/10| = |-0.5| = 0.0$,如果 $a = -15$,则 $a / 10 = -15 / 10 = q + r = (-2.0) + 0.5$,而 $|-15/10| = |-1.5| = -1.0$,我们看到,为了保证余数 $r$ 的范围在 $0 <= r < 1.0$,根据前面提到的负整数取整的定义,这里 $|a/10|$ 取整的值是比 $q$ 的值大 1 的。而 $q$ 的值正好我们在32位无符号整型所得的结果,我们要计算的是 $|a/10|$,所以只需要在 $q$ 值的结果上再加 1 即可。所以有了上面把EDX的符号位右移31位,再跟原EDX值累加的过程,最终累加的结果即为最后所求的 $|a/10|$ 值。
结论:当除数是常数时,除非你要计算的数值必须强制使用32位有符号整型,否则尽量使用32位无符号整型,因为32位有符号整型的常量除法会比无符号整型多两条指令,一条位移,一条ADD(加法)指令。
结束语
经过上面的推演,我们已经掌握了优化时用来相乘的系数以及位移(右移)的位数,可是为什么有的编译器把32位无符号整型的常量除法 /10 也优化成:Value / 10 ~= [ [ (Value * 0x66666667) / 2^32 ] / 2^2 ],这个道理很简单,只要能够满足被除数 a 在 0 ~ 2^32-1 范围内的误差都不大于 1/c 的话,不管你相乘的数是多少,最终的结果都是成立的。
/ 常数 和 % 常数 是等价的:其实这个优化常用于 itoa() 函数里,其实大多数情况下,都不会以 /10, /5, /3 的形式出现,多数是跟 % 10, % 5, % 3 一起出现的,如果同时做 /10, % 10 的运算,这两个运算是可以合并为一次的常数除法优化的,因为 % 10 只不过是 / 10 的求余过程,而得到了 /10,则 % 10 只是一个计算 $r = a - c * q$ 的过程,多一条乘法和一条减法指令而已。而Windows的 itoa() 函数是需要指定 radix(基) 的,10进制必须指定 radix = 10, 因为 radix 是一个变量,因此其内部使用的是 div 指令,这是一个很糟糕的函数。
还有很多的技巧,比如:sprintf()的实现代码里,一般都会通过一个变量 base 的改变来实现一个数转换为8进制,10进制或16进制,即令 base = 8; base = 10; base = 16; 但是编译器在处理 base = 8, 16 的时候是可以优化为位移的,但很奇怪的是,当 base = 10 的时候使用的却是 div 指令,这个特点在 Visual Studio 各个版本里都是如此,包括最新的 VS 2013, 2014,效率是打折扣的。GCC 和 clang 上我未求证,我猜 clang 上有可能能正确优化(当然可能是有前提条件的),有空可以研究一下。但是其实这个问题是可以通过修改代码来解决的,我们对每个部分的base都用常量来代替就可以了,这样就不依赖于编译器优化,因为都指定为常量了,编译器就明白怎么做了,没有歧义。
Jimi
这里做个小广告,推荐一下我的一个项目,我叫它 Jimi,Github地址为:https://github.com/shines77/jimi/ ,目标是实现一个高性能,实用,可伸缩,接口友好,较接近Java, CSharp的C/C++类库。一开始的灵感来自于OSGi.Net,http://www.iopenworks.com,原意是想实现像OSGi(Open Service Gateway Initiative)那样可伸缩的可任意搭配的C++类库,所以原本是想叫Jimu,也考虑过叫Jimmy,不过都不太好,所以改成现在这个名字。由于实现Java那样的OSGi对于C++目前是不太可行的(由于效率和语言本身的问题),所以方向也变了。里面包含了上面我提到的一些对 itoa() 和 sprintf() 的优化技巧,虽然还很多东西还不完整,也未做什么推广,但是里面有很多实用的技巧,等待你去发现。
参考文献
[讨论] B计划之大数乘以10,除以10的快速算法的讨论和实现 by liangbch
http://bbs.emath.ac.cn/thread-521-3-1.html
[CSDN论坛]利用移位指令来实现一个数除以10
http://bbs.csdn.net/topics/320096074
更新记录
2014/12/29:
根据网友 BillGan 的建议,修改了误差分析的过程,衔接性更好更容易理解。
2014/12/30:
修正被除数和除数称呼弄反的问题,特别感谢网友 Antineutrino 。
2014/12/31:
修正了推演步骤图片里"令"写成"另"的问题.
增加了“最终结论”的表述,这样便于了解怎么计算相乘系数 $m$ 和位移位数 $k$。
.< End >.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号