伪随机数生成算法

写在前面

伪随机数生成算法在计算机科学领域应用广泛，比如枪击游戏里子弹命中扰动、数据科学里对样本进行随机采样、密码设计、仿真领域等等，背后都会用到伪随机数生成算法。

说随机，那什么是随机呢？随机意味着不可预测，没有任何规律。谈随机数，一定是在序列当中，单拿出一个数谈随机是没有意义的。给一个数字序列，如果能在其中发现规律可以预测或以一定概率（大于“猜”的概率）预测接下来的数，那么这个序列就不是随机的。

在20世纪早期科学工作中就开始需要使用随机数，为了获取随机数，研究人员通过物理方式采集了成千上万的随机数，并发布给他人使用，比如RAND公司在1955年发布的《A Million Random Digits with 100,000 Normal Deviates》（百万乱数表）——亚马逊美国现在还有卖~。但是，通过物理方式采集“真”随机数并不高效，实时获取需要附加额外的随机数发生装置，而且获取速度缓慢、序列不可复现，如果将采集到随机数全保存下来则需要占用额外的存储空间，而且数量终究是有限的，于是大家开始寻求生成“伪”随机数的数学方法。伪随机数，顾名思义，即看起来是随机的但实际上不是，在不知其背后生成方式的情况下，生成的序列看上去毫无规律可言。

本文源自个人兴趣通过查阅参考文献整理所得，再加上个人的理解，大部分图片来自WIKI。

统计学检验

如何判断一个序列是否够随机呢？伪随机数生成算法多种多样，总要分出个孰好孰差，如何对各自的随机性进行定量评估呢？主要有两类方式，其出发点都是试图定量评估序列中是否隐含某种规律或模式：

• 实证检验。给定一个随机序列而不告知其背后的生成方式，尝试对观测到的分布进行拟合，以预测后面的序列,或者查看其中是否具有某些统计规律，比如查看分布是否均匀、连续值的相关性、某些数出现位置的间隔分布是否有规律等等。具体有\(\chi ^2\)检验、KS检验、Frequency test、Serial test等等。

• 理论检验。直接分析生成器的理论性质（已知生成方式），生成器通常需要配置一些参数，不同的参数会影响生成序列的质量，比如考察不同参数对随机序列周期的影响。

可在下一小节对理论检验一窥一二，但本文的重点不在于此，就不详细展开了，详细内容可见参考资料。

线性同余法

lin­ear con­gru­en­tial generator（LCG）线性同余法是最早最知名的伪随机数生成算法之一，曾被广泛应用，后逐渐被更优秀的算法替代，其通过如下递推关系定义：

\[X_{n+1} = (aX_n + c)\ mod \ m \]

其中，\(X\)为伪随机序列，

• \(m\)，\(m > 0\)，模数，显然其也是生成序列的最大周期
• \(a\)，\(0 < a < m\)，乘数
• \(c\)，\(0 \leq c < m\)，增量
• \(X_0\)，\(0 \leq X_0 < m\)，种子点（起始值）

当\(c = 0\)时，被称为multiplicative congruential generator (MCG)，如果\(c \neq 0\)，被称为mixed congruential generator。

线性同余法的参数应该被小心选取，否则生成的序列将非常糟糕，比如当\(a = 11, c = 0, m = 8, X_0=1\)时，得到的序列是 3、1、3、1、3……从1960s开始使用IBM的RANDU算法，参数设置为\(a = 65539, c = 0, m = 2^{31}\)，最终也被证明是糟糕的设计，因为\(65539 = 2 ^{16} + 3\)，可进一步推导得

\[X_{n+2} = (2^{16} + 3)X_{n+1} = (2^{16} + 3)^2 X_n = [6(2^{16} + 3) - 9]X_n=6X_{n+1}-9X_n \]

因为相邻3个数间存在这样的相关性，若将相邻3个数作为坐标绘制在3维坐标系里，会得到15个明显的平面

可见，获得的序列并不是那么随机，而且没有均匀地填充整个空间。线性同余法的参数很重要，一些平台和运行时库中采用的参数如下

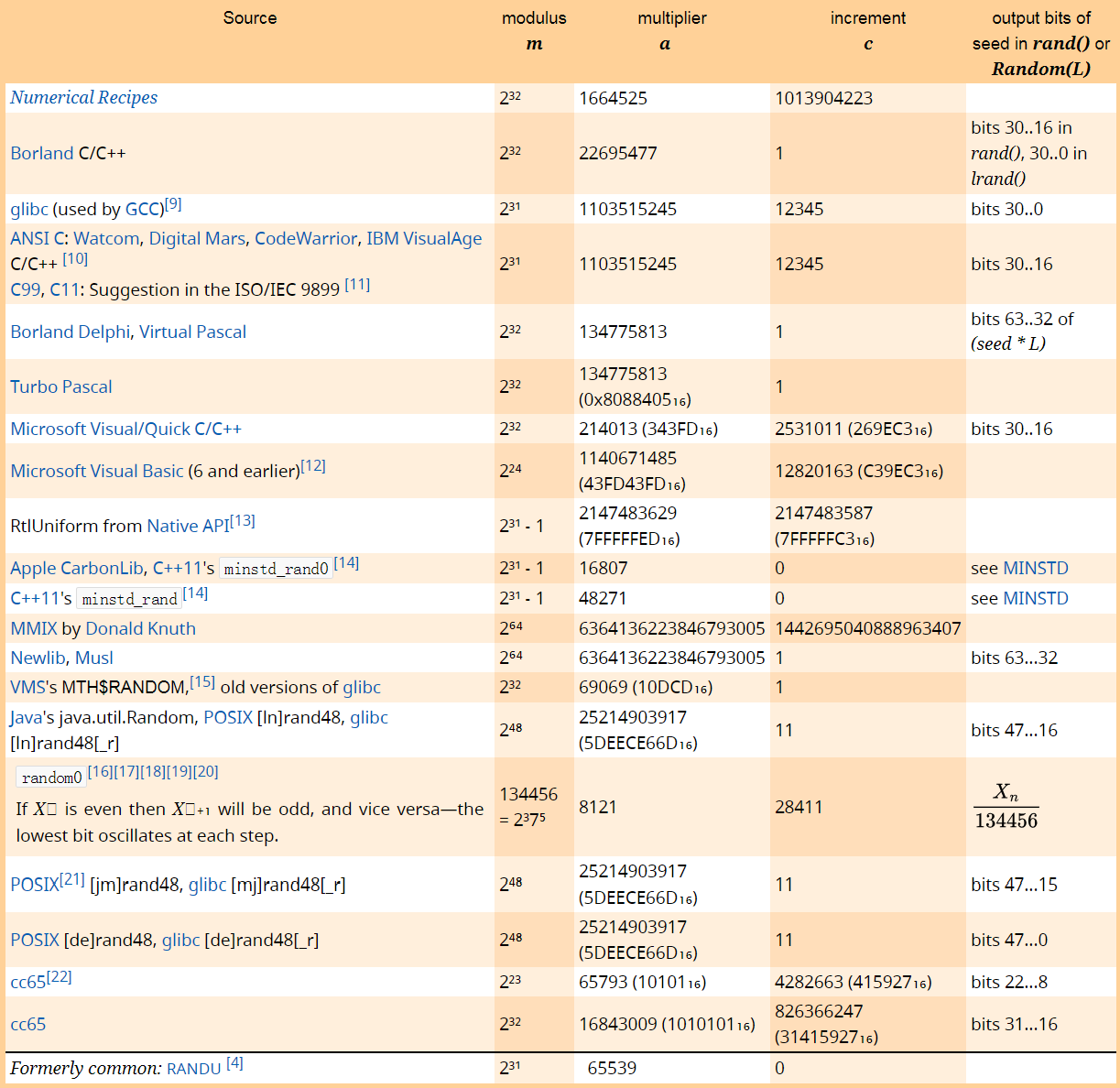
使用递推关系的方式带来了可复现的便利——只需要记住种子点就可以复现整个序列，而不需要去存储整个序列，但是带来的弊端就是相邻点之间的相关性，随意设置参数（像RANDU）可能让序列直落在几个稀疏的平面上，通常需要将\(m\)选取的足够大，同时避开2的整数次幂。

马特赛特旋转演算法

Mersenne Twister 马特赛特旋转演算法，是1997年提出的伪随机数生成算法，其修复了以往随机数生成算法的诸多缺陷，可快速生成高质量的伪随机数，且经过了广泛的统计学检验，目前在各种编程语言和库中已普遍存在或作为默认的伪随机数发生器，被认为是更可靠的伪随机数发生器。下图截自python的官方文档：

Mersenne Twister生成随机数的过程比线性同余法要复杂得多，图示化如下：

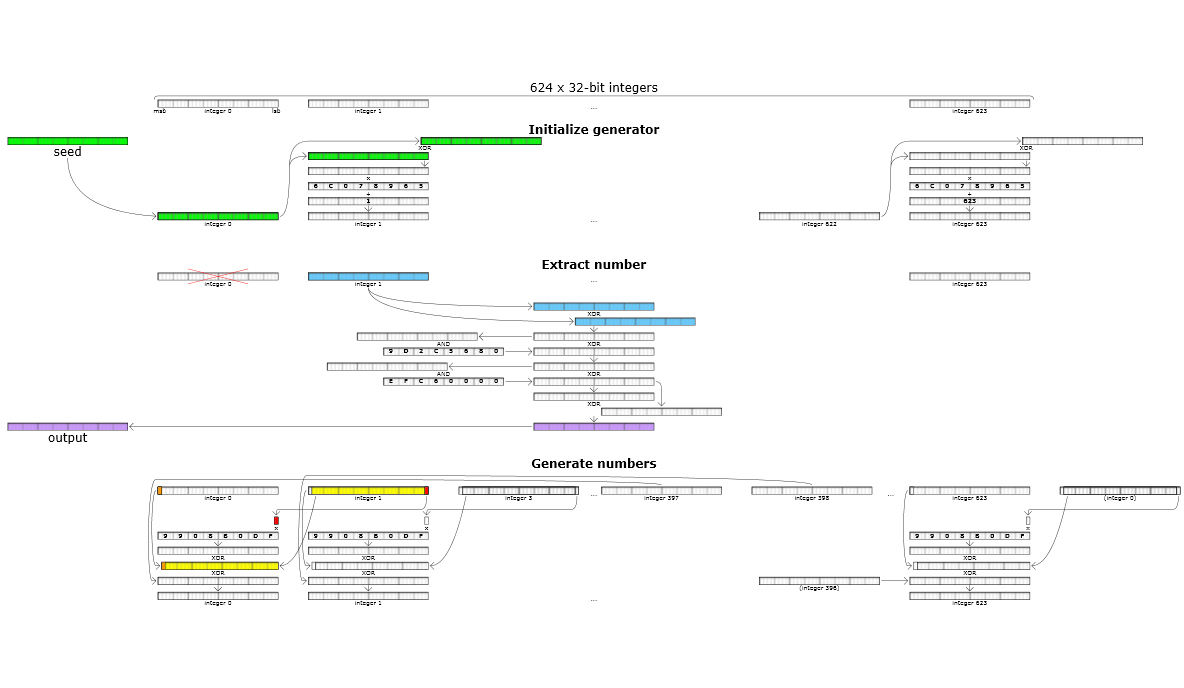
主要流程有3步是：

1. 初始化\(n\)个状态：根据给定的种子点\(x_0\)，通过移位、异或、乘法、加法等操作生成后续的\(n-1\)个状态\(x_1\)到\(x_{n-1}\)，bit位数为\(w\)
2. 生成伪随机数：根据当前状态，通过移位、与、异或操作生成随机数
3. 更新\(n\)个状态：每生成\(n\)个随机数后，在生成下一个随机数前，更新状态

具体参见伪代码（来自WIKI），如下：

// Create a length n array to store the state of the generator
int[0..n-1] MT
int index := n+1
const int lower_mask = (1 << r) - 1 // That is, the binary number of r 1's
const int upper_mask = lowest w bits of (not lower_mask)

// Initialize the generator from a seed
function seed_mt(int seed) {
    index := n
    MT[0] := seed
    for i from 1 to (n - 1) { // loop over each element
        MT[i] := lowest w bits of (f * (MT[i-1] xor (MT[i-1] >> (w-2))) + i)
    }
}

// Extract a tempered value based on MT[index]
// calling twist() every n numbers
function extract_number() {
    if index >= n {
        if index > n {
          error "Generator was never seeded"
          // Alternatively, seed with constant value; 5489 is used in reference C code
        }
        twist()
    }

    int y := MT[index]
    y := y xor ((y >> u) and d)
    y := y xor ((y << s) and b)
    y := y xor ((y << t) and c)
    y := y xor (y >> l)

    index := index + 1
    return lowest w bits of (y)
}

// Generate the next n values from the series x_i 
function twist() {
    for i from 0 to (n-1) {
        int x := (MT[i] and upper_mask)
                  + (MT[(i+1) mod n] and lower_mask)
        int xA := x >> 1
        if (x mod 2) != 0 { // lowest bit of x is 1
            xA := xA xor a
        }
        MT[i] := MT[(i + m) mod n] xor xA
    }
    index := 0
}

标准实现32bit版本称之为MT19937，参数设置如下：

• \((w, n, m, r) = (32, 624, 397, 31)\)
• \(a = \rm 9908B0DF_{16}\)
• \((u, d) = (11, \rm FFFFFFFF_{16})\)
• \((s, b) = (7, \rm 9D2C5680_{16})\)
• \((t, c) = (15, \rm EFC60000_{16})\)
• \(l = 18\)

后记

伪随机数生成算法有很多，远不止本文介绍的两种，还有middle-square method（1946）、Additive Congruential Method、xorshift（2003）、WELL（2006，对Mersenne Twister的改进）等等，本文只是从中选取具有代表性的两种，可阅读参考文献了解更多。

参考

• Random number generation
• Pseudorandom number generator
• Linear congruential generator
• RANDU
• Randomness tests
• Randomness Tests: A Literature Survey
• Testing Pseudo-Random Number Generators
• Validation of Pseudo Random Number Generators through Graphical Analysis
• How to Generate Pseudorandom Numbers
• NMCS4ALL: Random number generators

本文出自本人博客：伪随机数生成算法