从卷积拆分和分组的角度看CNN模型的演化
写在前面
如题,这篇文章将尝试从卷积拆分的角度看一看各种经典CNN backbone网络module是如何演进的,为了视角的统一,仅分析单条路径上的卷积形式。
形式化
方便起见,对常规卷积操作,做如下定义,
- I:输入尺寸,长H 宽W ,令长宽相同,即I=H=W
- M:输入channel数,可以看成是tensor的高
- K:卷积核尺寸K×K,channel数与输入channel数相同,为M
- N:卷积核个数
- F:卷积得到的feature map尺寸F×F,channel数与卷积核个数相同,为N
所以,输入为M×I×I的tensor,卷积核为N×M×K×K的tensor,feature map为N×F×F的tensor,所以常规卷积的计算量为
特别地,如果仅考虑SAME padding且stride=1的情况,则F=I,则计算量等价为
可以看成是(K×K×M)×(N×I×I),前一个括号为卷积中一次内积运算的计算量,后一个括号为需要多少次内积运算。
参数量为
网络演化
总览SqueezeNet、MobileNet V1 V2、ShuffleNet等各种轻量化网络,可以看成对卷积核M×K×K 进行了各种拆分或分组(同时引入激活函数),这些拆分和分组通常会减少参数量和计算量,这就为进一步增加卷积核数量N让出了空间,同时这种结构上的变化也是一种正则,通过上述变化来获得性能和计算量之间的平衡。
这些变化,从整体上看,相当于对原始FLOPS=K×K×M×N×I×I做了各种变换。
下面就从这个视角进行一下疏理,简洁起见,只列出其中发生改变的因子项,
-
Group Convolution(AlexNet),对输入进行分组,卷积核数量不变,但channel数减少,相当于
M→MG
-
大卷积核替换为多个堆叠的小核(VGG),比如5×5替换为2个3×3,7×7替换为3个3×3,保持感受野不变的同时,减少参数量和计算量,相当于把 大数乘积 变成 小数乘积之和,
(K×K)→(k×k+⋯+k×k)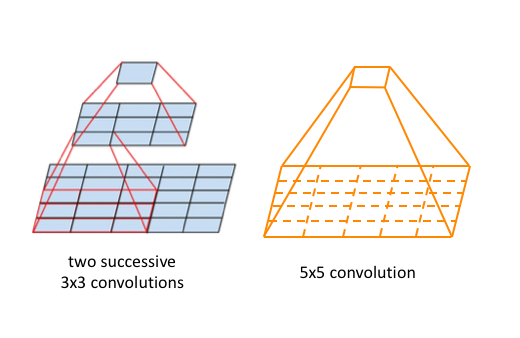
-
Factorized Convolution(Inception V2),二维卷积变为行列分别卷积,先行卷积再列卷积,
(K×K)→(K×1+1×K)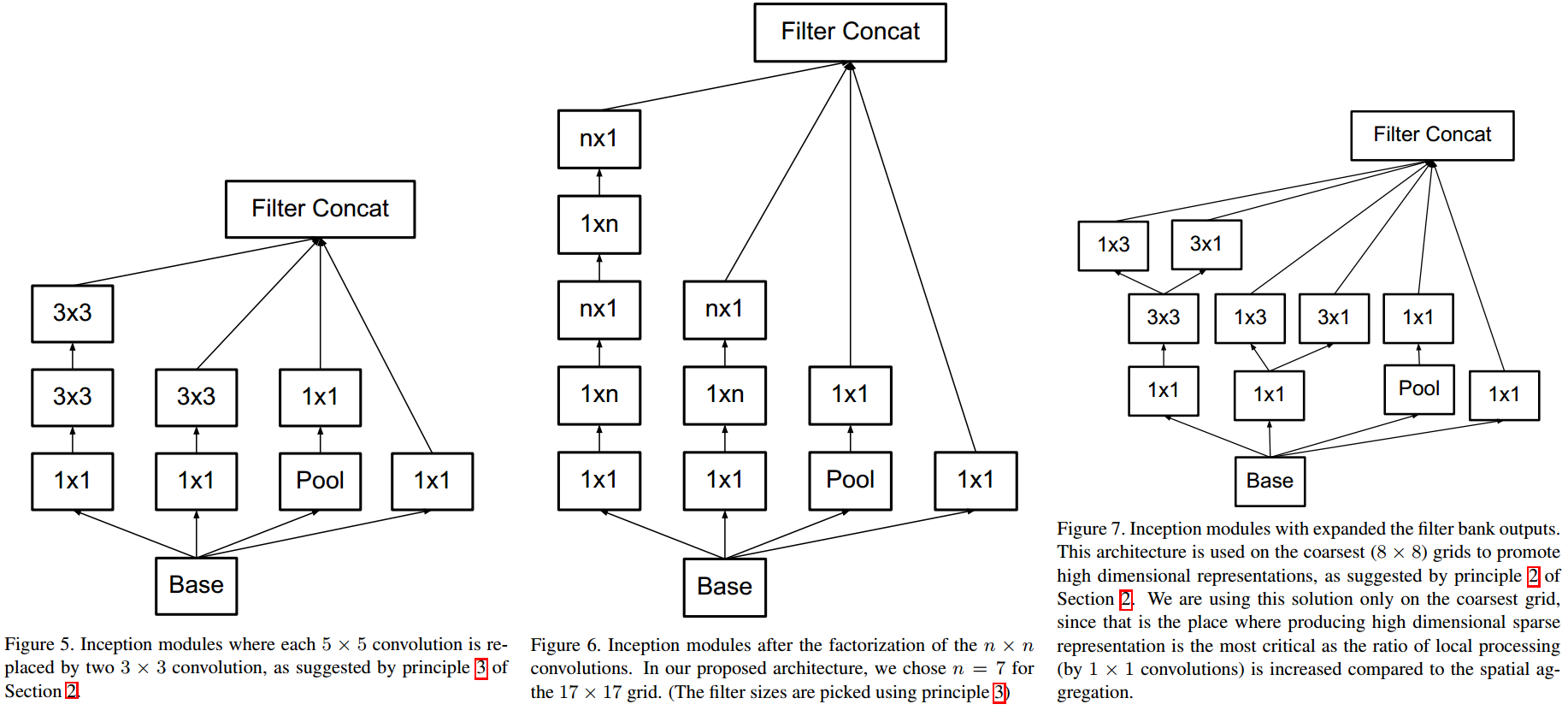
-
Fire module(SqueezeNet),pointwise+ReLU+(pointwise + 3x3 conv)+ReLU,pointwise降维,同时将一定比例的3×3卷积替换为为1×1,
(K×K×M×N)→(M×Nt+Nt×(1−p)N+K×K×Nt×pN)K=3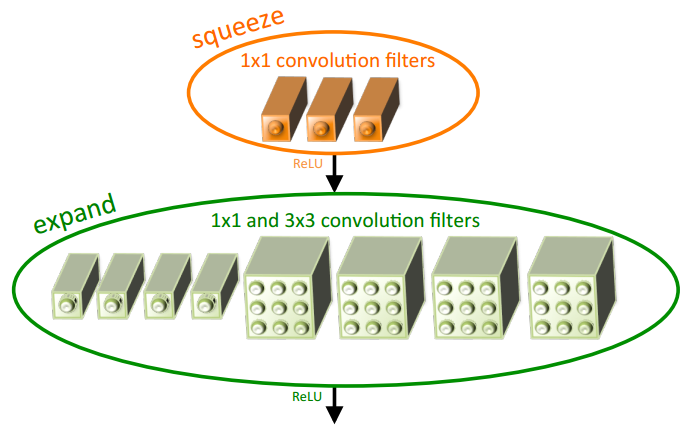
-
Bottleneck(ResNet),pointwise+BN ReLU+3x3 conv+BN ReLU+pointwise,类似于对channel维做SVD,
(K×K×M×N)→(M×Nt+K×K×Nt×Nt+Nt×N)t=4
-
ResNeXt Block(ResNeXt),相当于引入了group 3×3 convolution的bottleneck,
(K×K×M×N)→(M×Nt+K×K×NtG×Nt+Nt×N)t=2, G=32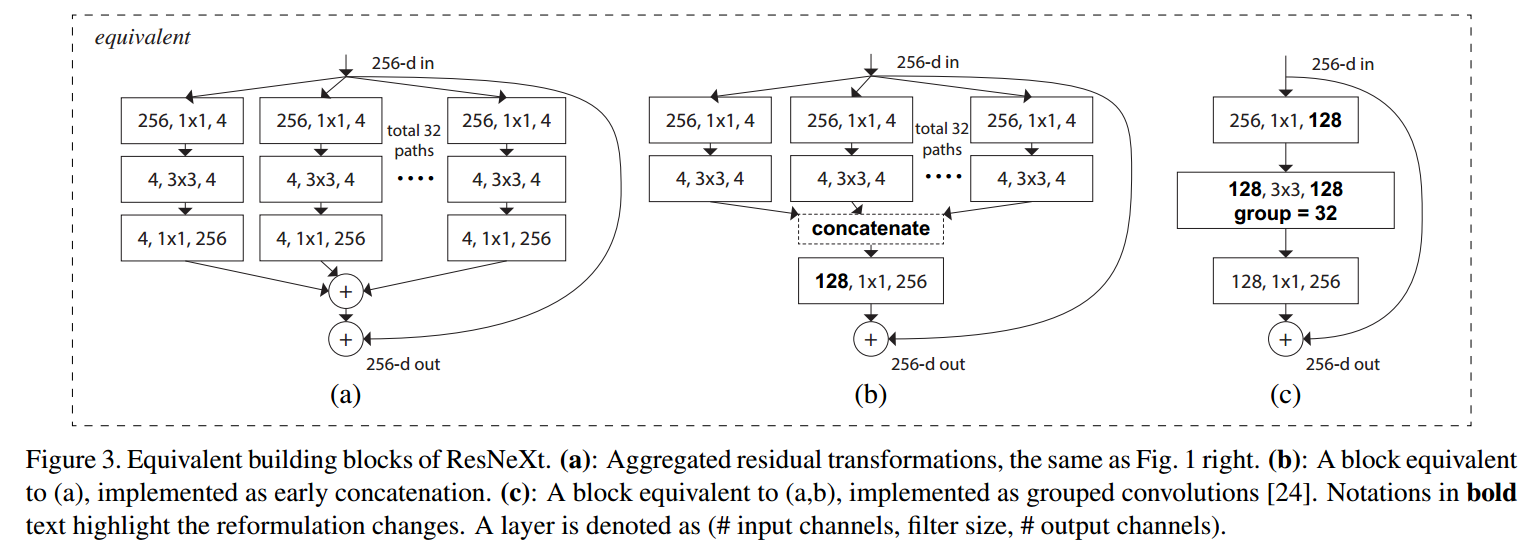
-
Depthwise Separable Convolution(MobileNet V1),depthwise +BN ReLU + pointwise + BN ReLU,相当于将channel维单独分解出去,
(K×K×N)→(K×K+N)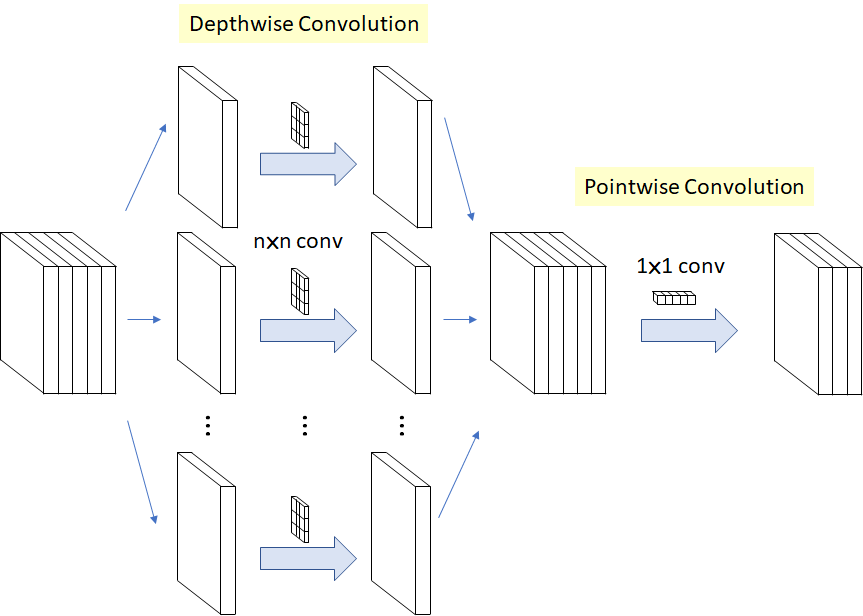
-
Separable Convolution(Xception),pointwise + depthwise + BN ReLU,也相当于将channel维分解出去,但前后顺序不同(但因为是连续堆叠,其实跟基本Depthwise Separable Convolution等价),同时移除了两者间的ReLU,
(K×K×M)→(M+K×K)但实际在实现时还是depthwise + pointwise + ReLU。。。
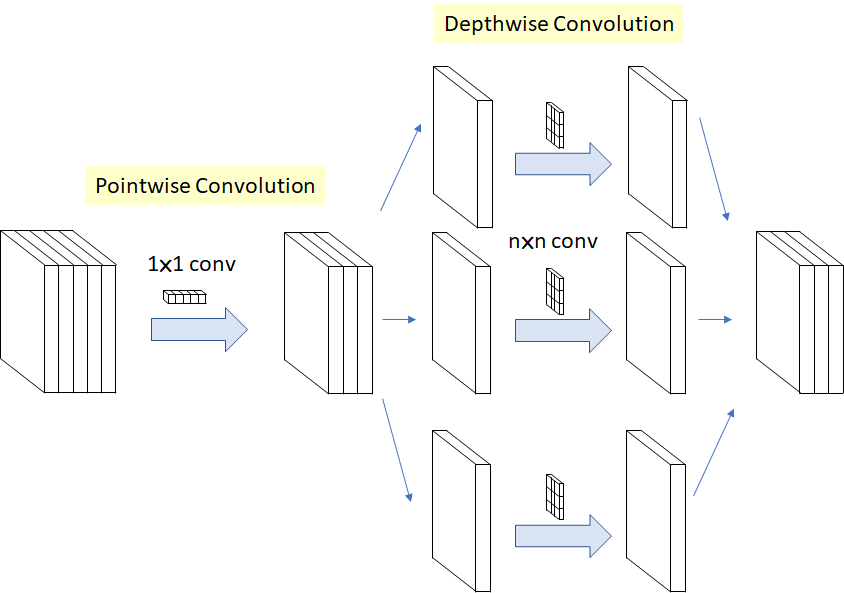
-
pointwise group convolution and channel shuffle(ShuffleNet),group pointwise+BN ReLU+Channel Shuffle+depthwise+BN+group pointwise+BN,相当于bottleneck中2个pointwise引入相同的group,同时3×3 conv变成depthwise,也就是说3个卷积层都group了,这会阻碍不同channel间(分组间)的信息交流,所以在第一个group pointwise后加入了channel shuffle,即
(K×K×M×N)→(MG×Nt+channel shuffle+K×K×Nt+NtG×N)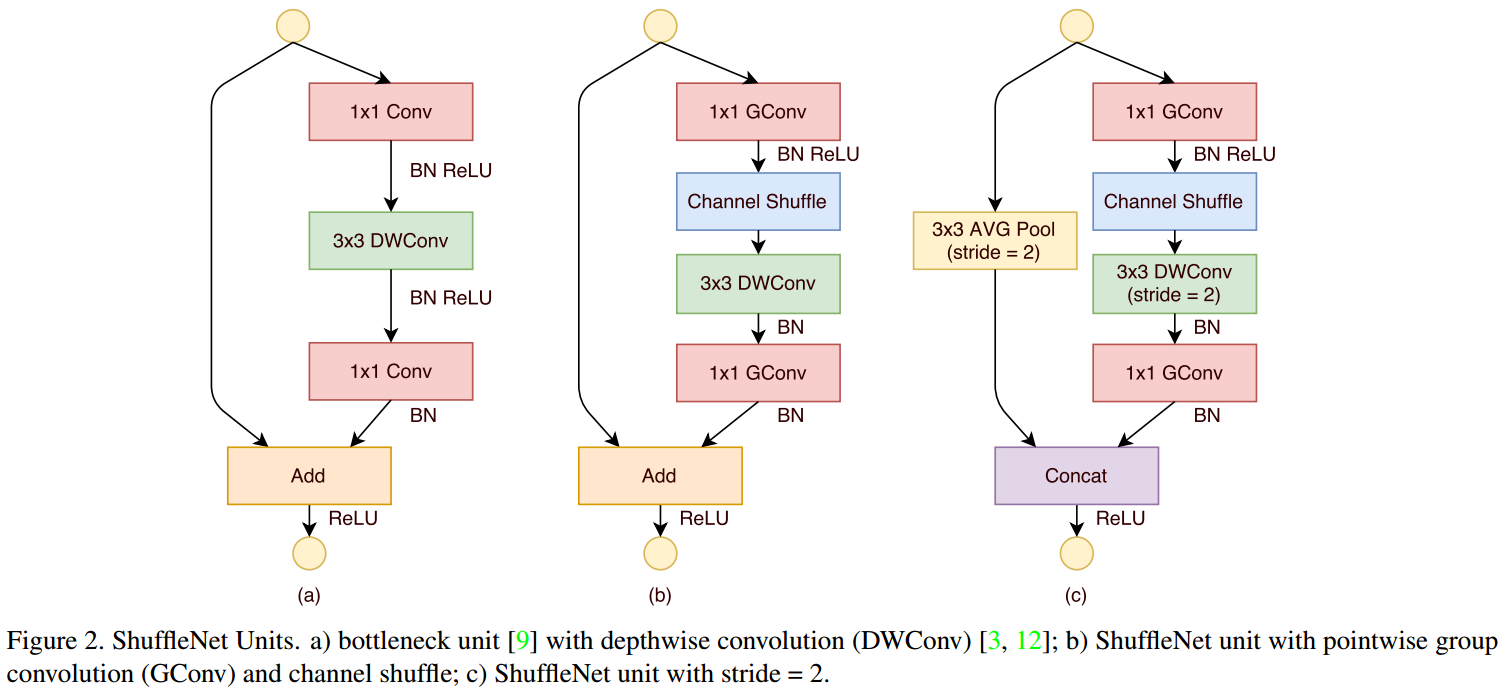
-
Inverted Linear Bottleneck(MobileNet V2),bottleneck是先通过pointwise降维、再卷积、再升维,Inverted bottleneck是先升维、再卷积、再降维,pointwise+BN ReLU6+depthwise+BN ReLU6+pointwise+BN,
(K×K×M×N)→(M×tM+K×K×tM+tM×N)t=6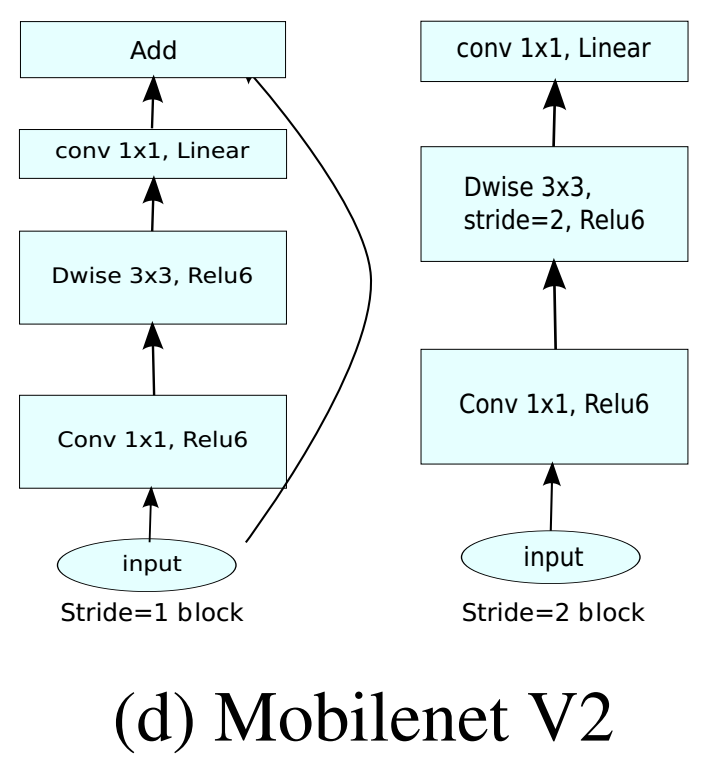
小结
最后小结一下,早期的CNN由一个个常规卷积层堆叠而成,而后,开始模块化,由一个个 module构成,module的演化,可以看成是不停地在常规卷积的计算量FLOPS=K×K×M×N×I×I上做文章。
- 拆分:卷积核是个3 D 的tensor,可以在不同维度上进行拆分,行列可拆分,高也可拆分,还可以拆分成多段串联。
- 分组:如果多个卷积核放在一起,可以构成4D的tensor,增加的这一数量维上可以分组group。
不同拆分和分组的方式排列组合就构成了各种各样的module。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 你所不知道的 C/C++ 宏知识
· 聊一聊 操作系统蓝屏 c0000102 的故障分析
· SQL Server 内存占用高分析
· .NET Core GC计划阶段(plan_phase)底层原理浅谈
· .NET开发智能桌面机器人:用.NET IoT库编写驱动控制两个屏幕
· 我干了两个月的大项目,开源了!
· 推荐一款非常好用的在线 SSH 管理工具
· 千万级的大表,如何做性能调优?
· 聊一聊 操作系统蓝屏 c0000102 的故障分析
· .NET周刊【1月第1期 2025-01-05】
2015-05-14 python中的编码与解码