博弈论(SG) hdu5724
百度搜一下博弈论 由感性认识到理性认识的论文
理论铺垫:
1、定义P-position和 N-position:其中P代表Previous,N代表Next。直观的说,上一次move的人有必胜策略的局面是P-position,也就是“先 手必败”,现在轮到move的人有必胜策略的局面是N-position,也就是“先手可保证必胜”。
(1).无法进行任何移动的局面(也就是terminal position)是P-position;
(2).可以移动到P-position的局面是N-position;
(3).所有移动都导致N-position的局面是P-position。
2、P/N状态有如下性质:
(1)、若面临末状态者为获胜则末状态为胜态否则末状态为必败态。
(2)、一个局面是胜态的充要条件是该局面进行某种决策后会成为必败态。
(3)、一个局面是必败态的充要条件是该局面无论进行何种决策均会成为胜态
3、P点: 即必败点,某玩家位于此点,只要对方无失误,则必败;
N点: 即必胜点,某玩家位于此点,只要自己无失误,则必胜。
4、取石子游戏算法实现
步骤1:将所有终结位置标记为必败点(P点);
步骤2: 将所有一步操作能进入必败点(P点)的位置标记为必胜点(N点)
步骤3:如果从某个点开始的所有一步操作都只能进入必胜点(N点) ,则将该点标记为必败点(P点) ;
步骤4: 如果在步骤3未能找到新的必败(P点),则算法终止;否则,返回到步骤2
/*
a.如果当前是P点,那么一步(向前)可以走到的都是N点
b.如果当前点未标明P/N属性,那么看看该点向后走是不是都只能到达N点,如果是,那么该点是P点。
c.如果该点是N点,倒无法确定什么。
如果没办法标一个点,那么异常结束。
*/
几种常见类型详解:
一、巴什博弈
1、问题模型:只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个,最后取光者得胜。
2、解决思路:当n=m+1时, 由于一次最多只能取m个,所以无论先取者拿走多少个,后取者都能够一次拿走剩余的物品,后者取胜,所以当一方面对的局势是n%(m+1)=0时,其面临的 是必败的局势。所以当n=(m+1)*r+s,(r为任意自然数,s≤m)时,如果先取者要拿走s个物品,如果后取者拿走x(≤m)个,那么先取者再拿走 m+1-k个,结果剩下(m+1)(r-1)个,以后保持这样的取法,那么先取者肯定获胜。总之,要保持给对手留下(m+1)的倍数,就能最后获胜。
3、变形:条件不变,改为最后取光的人输。
结论:当(n-1)%(m+1)==0时后手胜利。
4、题目练习:HDOJ:2188 2149 1846
二、威佐夫博奕
1、问题模型:有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
2、解决思路:A:设(ai,bi) (ai ≤bi ,i=0,1,2,…,n)表示两堆物品的数量并称其为局势,如果甲面对(0,0),那么甲已经输了,这种局势我们称为奇异局势。前几个奇异局势是: (0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。任给一个局势 (a,b),如下公式判断它是不是奇异局势: ak =[k(1+√5)/2],bk= ak + k (k=0,1,2,…,n 方括号表示取整函 数)。(证明见百度百科)
B:详见 http://www.freopen.com/?p=10512)
3、满足上公式的局势性质:
(1)任何自然数都包含在一个且仅有一个奇异局势中。
由于ak是未在前面出现过的最小自然数,所以有ak > ak-1 ,而 bk= ak + k > ak-1 + k-1 = bk-1 > ak-1 。所以性质成立。
(2)任意操作都可将奇异局势变为非奇异局势。
若只改变奇异局势(ak,bk)的某一个分量,那么另一个分量不可能在其他奇异局势中,所以必然是非奇异局势。如果使(ak,bk)的两个分量同时减少,则由于其差不变,且不可能是其他奇异局势的差,因此也是非奇异局势
(3)采用适当的方法,可以将非奇异局势变为奇异局势。
假设面对的局势是(a,b),若 b = a,则同时从两堆中取走 a 个物体,就变为了奇异局势(0,0);如果a = ak ,b & gt; bk,那么,取走b – bk个物体,即变 为奇异局势;如果 a = ak , b < bk ,则同时从两堆中拿走 ak – ab – ak个物体,变为奇异局势 ( ab – ak , ab – ak+ b – ak);如果a > ak , b= ak + k,则从第一堆中拿走多余的数量a – ak 即可;如果a < ak ,b= ak + k,分两种情况,第一 种,a=aj (j < k),从第二堆里面拿走 b – bj 即可; 第 二种,a=bj (j < k),从第二堆里面拿走 b – aj 即可。
4、结论:两个人如果都采用正确操作,那么面对非奇异局势,先拿者必胜;反之,则后拿者取胜。
5、练习:poj 1067
三、Fibonacci博弈
1、问题模型:
有一堆个数为n的石子,游戏双方轮流取石子,满足:
(1)先手不能在第一次把所有的石子取完;
(2)之后每次可以取的石子数介于1到对手刚取的石子数的2倍之间(包含1和对手刚取的石子数的2倍)。 约定取走最后一个石子的人为赢家。
2、解决思路:
当n为Fibonacci数时,先手必败。即存在先手的必败态当且仅当石头个数为Fibonacci数。
证明:根据“Zeckendorf定理”(齐肯多夫定理):任何正整数可以表示为若干个不连续的Fibonacci数之和。如 n=83 = 55+21+5+2,我们看看这个分解有什么指导意义:假如先手取2颗,那么后手无法取5颗或更多,而5是一个Fibonacci数,那么 一定是先手取走这5颗石子中的最后一颗,同理,接下去先手取走接下来的后21颗中的最后一颗,再取走后55颗中的最后一颗,那么先手赢。
反证:如果n是Fibonacci数,如n=89:记先手一开始所取的石子数为y
(1)若y>=34颗(也就是89的向前两项),那么一定后手赢,因为89-34=55=34+21<2*34。
(2)y<34时剩下的石子数x介于55到89之间,它一定不是一个Fibonacci数,把x分解成Fibonacci 数:x=55+f[i]+…+f[j],若,如果f[j]<=2y,那么对B就是面临x局面的先手,所以根据之前的分析,后手只要先取f[j]个即 可,以后再按之前的分析就可保证必胜。
3、练习题目:NYOJ 取石子游戏
四、尼姆博弈
1、问题模型:有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
2、解决思路:用(a,b,c)表示某种局势,显证(0,0,0)是第一种奇异局势,无论谁面对奇异局势,都必然失败。第二种奇异局势是(0,n,n),只要与对手拿走一样多的物品,最后都将导致(0,0,0)。
搞定这个问题需要把必败态的规律找出:(a,b,c)是必败态等价于a^b^c=0(^表示异或运算)。
证明:(1)任何p(a,b,c)=0的局面出发的任意局面(a,b,c’);一定有p(a,b,c’)不等于0。否则可以得到c=c’。
(2)任何p(a,b,c)不等于0的局面都可以走向 p(a,b,c)=0的局面
(3)对于 (4,9,13) 这个容易验证是奇异局势
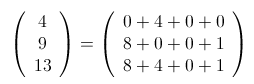
其中有两个8,两个4,两个1,非零项成对出现,这就是尼姆和为 零的本质。别人要是拿掉13里的8或者1,那你就拿掉对应的9 中的那个8或者1;别人要是拿 掉13里的4,你就拿掉4里的4; 别人如果拿掉13里的3,就把10作分解,然后想办法满 足非零项成对即可。
3、推广一:如果我们面对的是一个非奇异局势(a,b,c),要如何变为奇异局势呢?假设 a < b< c,我们只要将 c 变为 a^b,即可,因为有如下的运算结果: a^b^(a^b)=(a^a)^(b^b)=0^0=0。要将c 变为a^b,只从 c中减去 c-(a^b)
4、推广二:当石子堆数为n堆时,则推广为当对每堆的数目进行亦或之后值为零是必败态。
5、练习:hdoj 1847
五、公平组合博弈(Impartial Combinatori Games)
1、定义:
(1)两人参与。
(2)游戏局面的状态集合是有限。
(3)对于同一个局面,两个游戏者的可操作集合完全相同
(4)游戏者轮流进行游戏。
(5)当无法进行操作时游戏结束,此时不能进行操作的一方算输。
(6)无论游戏如何进行,总可以在有限步数之内结束。
2、模型:给定一个有向无环图和一个起始顶点上的一枚棋子,两名选手交替的将这枚棋子沿有向边进行移动,无法移动者判负。事实上,这个游戏可以认为是所有公平组合游戏(Impartial Combinatori Games)的抽象模型。其实,任何一个ICG都可以通过把每个局势看成一个顶点,对每个局势和它的子局势连一条有向边来抽象成这个“有向图游戏”。
3、解决思路:
现在,假定我们给出两个游戏G1 和 G2。如果我们只知道单个游戏的P-状态和N-状态我们能够正确地玩好游戏和G1 + G2吗?答案是否定的。不难看出两个P-状态的和总是P-状态,P-状态和N-状态的和总是N-状态。但是两个N-状态的和既可能是P-状态也可能是N-状态。因此,只知道单个游戏的P-状态和N-状态是不够的。
为了正确地玩好游戏和我们需要推广P-状态和N-状态,它就是Sprague-Grudy函数(或者简称为g函数)
4、Sprague-Grudy定理:
令N = {0, 1, 2, 3, ...} 为自然数的集合。Sprague-Grundy 函数给游戏中的每个状态分配了一个自然数。结点v的sg值等于没有在v的后继的sg值中出现的最小自然数.
形式上:给定一个有限子集 S ⊂ N,令mex S(最小排斥值)为没有出现在S中的最小自然数。定义mex(minimal excludant)运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图,定义关于图的每个顶点的Sprague-Garundy函数g如下:g(x)=mex{ g(y) | y是x的后继 }。
5、性质:
(1)所有的终结点所对应的顶点,其SG值为0,因为它的后继集合是空集——所有终结点是必败点(P点)。
(2)对于一个g(x)=0的顶点x,它的所有后继y都满足g(y)!=0——无论如何操作,从必败点(P点)都只能进入必胜点(N点)//对手走完又只能把N留给我们。
(3)对于一个g(x)!=0的顶点,必定存在一个后继点y满足g(y)=0——从任何必胜点(N点)操作,至少有一种方法可以进入必败点(P点)//就是那种我们要走的方法。
6、应用:
(1)可选步数为1-m的连续整数,直接取模即可,SG(x) = x % (m+1);
(2)可选步数为任意步,SG(x) = x;
(3)可选步数为一系列不连续的数,用mex(计算每个节点的值)
7、练习:hdoj 1847 1536 3980
下面说一下hdu5724的代码
典型的sg值博弈的问题,一步步操作求相应的sg值就行
#include <stdio.h> #include<algorithm> #include<string.h> #include<iostream> using namespace std; int tt,n,m,q,t[(1<<20)+5],mex[1<<20]; int g(int u)//其实就是用递归的方法,从小到大把所有的t[u]求出来 { if(t[u]!=-1) return t[u]; int min1=-1,cnt=0,mex[30]; int ans=u; memset(mex,0,sizeof(mex));//因为每一次操作之后只有20个数,所以补集的最小值肯定在前20个数里 while(ans%2==1&&ans>0){ ans/=2; cnt++; } min1=cnt; while(ans>0) { if(ans%2==1) mex[t[u-(1<<cnt)+(1<<min1)]]=1; if(ans%2==0) min1=cnt; ans/=2; cnt++; } for(int i=0;; i++) if(!mex[i]) return i; } void init() { memset(t,-1,sizeof(t)); t[0]=0; int sum=0; for(int i=0; i<20; i++) { sum+=1<<i; t[sum]=0; } for(int i=1; i<(1<<20); i++) { t[i]=g(i); } } int main() { freopen("in.txt","r",stdin); init(); cin>>tt; while(tt--) { scanf("%d",&n); int ans=0; int i,j; for(i=1; i<=n; i++) { scanf("%d",&m); int sum=0; for(j=1; j<=m; j++) { scanf("%d",&q); sum+=(1<<(20-q)); } ans^=t[sum]; } //cout<<t[2]<<" "<<t[4]<<endl; if(!ans) cout<<"NO"<<endl; else cout<<"YES"<<endl; } return 0; }



