并查集（路径压缩法+启发式合并法）

我们从一道例题看起：洛谷P1551 亲戚。

问题很简单，给出一个亲戚关系图，规定 $x$ 和 $y$ 是亲戚， $y$ 和 $z$ 是亲戚，那么 $x$ 和 $z$ 也是亲戚，那么 $x$ 的亲戚都是 $y$ 的亲戚， $y$ 的亲戚也都是 $x$ 的亲戚，再给定 $P_{i}$ 和 $P_{j}$ ，询问他们是否是亲戚，输出 Yes 或 No。

人数，亲戚关系，询问次数 $\leq 5000$ 。

这样的亲戚关系图我们可以把它看作若干个集合，一个人就是一个元素，得知两个人是亲戚后，将他们各属于的集合合并即可，查询 $P_{i}$ 和 $P_{j}$ 是否是亲戚，就只要查询他们在不在同一个集合中。

因为一个元素只可能属于一个集合，所以我们可以为每一个集合选取一个代表元。这样子做，我们查询两个元素是否属于同一个集合就只需要比较他们各自的集合的代表元是否相同即可。

我们尝试实现合并集合和查询集合代表元这两个操作，查询集合代表元可以用数组标记将时间复杂度优化成 $O (1)$ ，而合并集合时需要改变其中一个集合中的所有元素的代表元，时间复杂度非常高，很明显需要优化。

这道题我们就可以使用并查集来解决，它的思路是，维护一个树形结构，对于同一个集合中的元素，把他们之间的关系构成一棵树，那么这棵树就有相同的根节点，我可以通过判断他们根节点是否相同，来判断他们是否处于同一个集合中。

1|0初始化

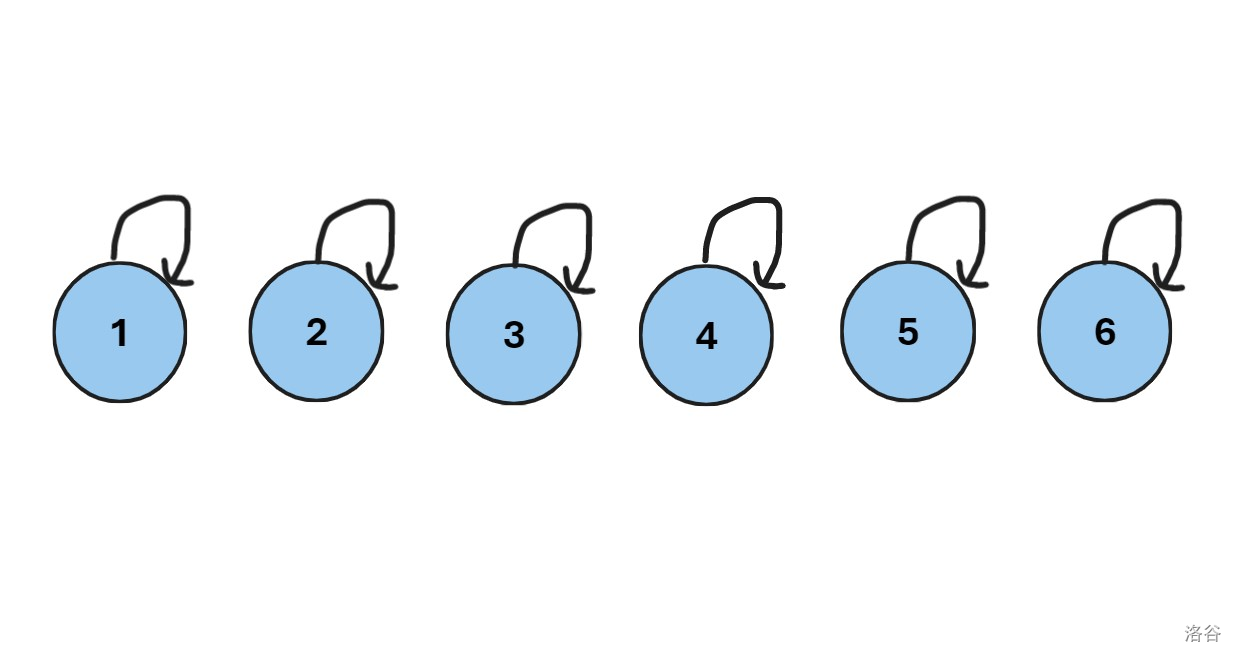
由于初始时每一个集合都只有一个元素，所以把这些集合都单独看作一棵树。

以这道题的样例为例：

有 $6$ 个人，也就是 $6$ 个集合， $6$ 棵树，每棵树的根是它自己。

写成代码就是：

int fa[MAXN];
void init(){
    for(int i=1;i<=n;i++){
    	fa[i]=i;
	}
}

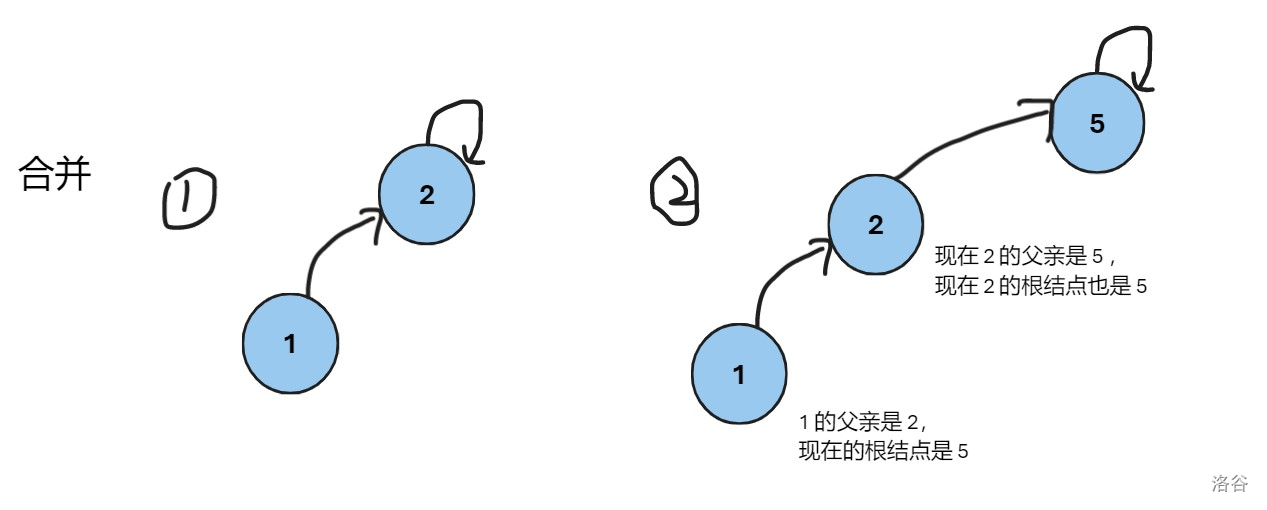
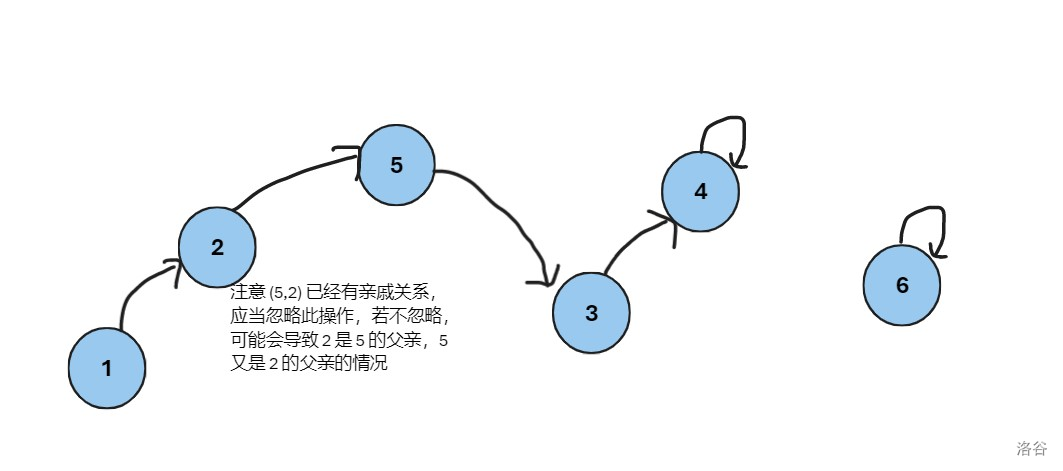
2|0合并

将两个集合合并，就是对两棵树合并，将其中一棵树的根结点变成另一棵树的根结点，如我们要合并 $(1, 2)$ 和 $(1, 5)$ ，如下图所示：

$5$ 次操作完成后如下图所示：

写成代码也很简单：

int findfa(int x){//求根结点
    return (fa[x]==x)?x:(fa[x]=findfa(fa[x]));
}
......
if(findfa(x)!=findfa(y)){
    fa[findfa(x)]=findfa(y);
}

3|0查询

还是对于上面那几棵树，查询 $(1, 4)$ 时，因为 $1$ 和 $4$ 都属于同一棵树上，他们的根结点都是 $4$ 。

int merge(int x,int y){
	if(findfa(x)==findfa(y)) return true;
	else return false;
}

合并和查询的 findfa 函数都使用路径压缩法，因为我们不管在合并还是查询操作，都只关心每棵树的根结点，我们就干脆不记录结点的父亲，只记录该结点所属的这棵树的根结点，并更新沿途经过结点的父亲为根结点即可，findfa 函数还有一种非递归形式，如下：

int findfa(int x){
	int rx=x;
	while(fa[rx]!=rx){
        rx=fa[rx];
    }
	while(fa[x]!=rx){
		int t=fa[x];
		fa[x]=rx;
		x=t;
    }
	return rx;
}

这样子，我们每次操作的时间复杂度只有 $O (\log n)$ （平均意义下）。

4|0启发式合并

上面那种路径压缩法，每一次合并，我们都会把一棵树的根设为另一棵树的根，这样就会把树摞得很高很高，因此，我们可以把两棵树中树高小的那棵树的根结点设为另一棵树的根，这样，只有树高一样时，合并后的树高才是他们其中的一个树高加 $1$ 。

具体代码实现如下：

void init(){
	for(int i=1;i<=n;i++){
        fa[i]=i;
        h[i]=1;//初始树高
	}
}
void merge(int x,int y){
	int rx=findfa(x),ry=findfa(y);
	if(rx==ry){
        return ;
    }
	if(h[rx]>h[ry]){
        swap(x,y);
        swap(rx,ry); 
    }
	fa[rx]=ry;
	h[ry]=max(h[ry],h[rx]+1);
}

这样，相比于路径压缩法，启发式合并法的单次操作优化到 $O (\log n)$ （稳定）。

当我们将路径压缩法和启发式合并法放在一起，单次操作的时间复杂度只有 $O (α (n))$ ，但是任何一道 OI 题均不会区分 $O (α (n))$ 和 $O (\log n)$ ，因此我们用任意一种方法均可。

该题的路径压缩法代码如下：

/*Written by smx*/
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e4+5;
int n,m,q;
int fa[MAXN];
void init(){
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
}
int findfa(int x){
	return (fa[x]==x)?x:(fa[x]=findfa(fa[x]));
}
int merge(int a,int b){
	if(findfa(a)==findfa(b)){
		return true;
	}else{
		return false;
	}
}
int main(){
	//freopen(".in","r",stdin);
	//freopen(".out","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>m>>q;
	init();
	while(m--){
		int a,b;
		cin>>a>>b;
		fa[findfa(a)]=findfa(b);
	}
	while(q--){
		int a,b;
		cin>>a>>b;
		if(merge(a,b)){
			cout<<"Yes\n";
		}else{
			cout<<"No\n";
		}
	}
	return 0;
}

__EOF__

本文作者：shimingxin1007
本文链接：https://www.cnblogs.com/shimingxin1007/p/18363102.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！