映射

设$X$和$Y$是两个非空集合，如果存在一个法则$f$，使得对$X$中每一个元素$x$
根据法则$f$，在$Y$中有唯一确定的元素$y$与之对应，则称$f$为从$X$到$Y$的映射，记作：$f:X \to Y$

其中$y$称为元素$x$在映射$f$下的象，记作：$f(x)$，即$y=f(x)$

元素$x$称为$y$在映射$f$下的一个原象

集合$X$称为映射$f$的定义域，记作：$D_{f}$

$X$中所有元素的象所组成的集合称为映射$f$的值域，记作：$R_{f}$或$f(X)$，即$R_f=f(X)=\{f(x)|x \in X\}$

 

满射
　　设有映射$f:X \rightarrow Y$，如果$R_f=Y$，即$Y$中任一元素$y$都是$X$中的某个元素$x$的象：$y=f(x)$，则称$f$为$X$到$Y$的满射
　　$f:X \rightarrow Y$是满射$\Leftrightarrow \forall y \in Y，\exists x \in X(y=f(x))$

单射
　　设有映射$f:X \rightarrow Y$，如果对集合$X$中任意两个不同的元素$x_{1} \neq x_{2}$，它们的象也不同：$f(x_{1}) \neq f(x_{2})$，则称$f$为$X$到$Y$的单射
　　$f:X \rightarrow Y$是单射$\Leftrightarrow \forall x_{1}，x_{2} \in X(x_{1} \neq x_{2}) \Rightarrow f(x_{1}) \neq f(x_{2})$

双射
　　如果映射$f:X \rightarrow Y$既是单射，又是满射，则称$f$为$X$到$Y$的双射(或一一映射)
　　如果$f:X \rightarrow Y$是单射，则$f:X \rightarrow R_{f}$为双射

逆映射

　　设$f:X \rightarrow Y$是单射(则：$f:X \rightarrow R_{f}$为双射)，则对每一个$y \in R_{f}$，有唯一的$x \in X$，使得$f(x)=y$
　　因此我们可以定义一个映射$\varphi：R_{f} \rightarrow X$，使$\varphi(y)=x(y=f(x))$
　　这个映射$\varphi$称为$f$的逆映射，记作$f^{-1}:R_{f} \rightarrow X$，即$f^{-1}(y)=x(y=f(x))$.$f_{-1}$的定义域为$R_{f}$，值域为$X$
　　设$f:X \rightarrow Y$是双射，则$f$的逆映射$f^{-1}:Y \rightarrow X$也是双射，且$f^{-1}[f(x)]=x(\forall x \in X)$，$f[f^{-1}(y)]=y(\forall y \in Y)$
　　映射$f:X \rightarrow Y$有逆映射(可逆)的充分必要条件是$f$为单射

 

满射，单射和双射的比较

           

 

  

 

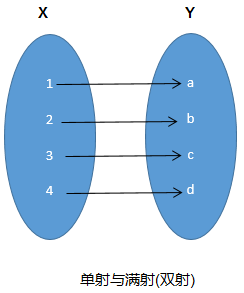
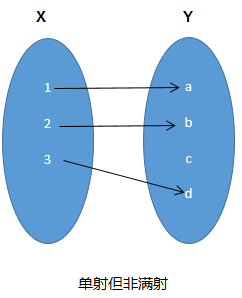
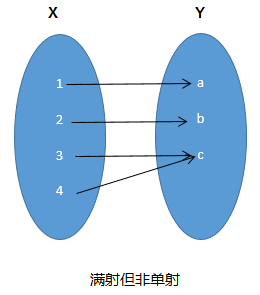
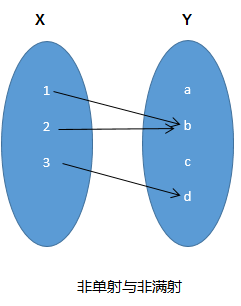
　　单射就是只能一对一，不能多对一

　　满射只要Y中的元素在X中都能找到原像就行了(一对一，多对一都行).

　　双射就是既是单射又是满射(一个对一个,每个都不漏掉).