SGD的优化:SGD+Momentum、Nesterov Momentum、AdaGrad、 RMSProp、Adam
1. SGD的不足:
①呈“之”字型,迂回前进,损失函数值在一些维度的改变得快(更新速度快),在一些维度改变得慢(速度慢)- 在高维空间更加普遍

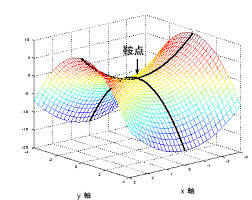
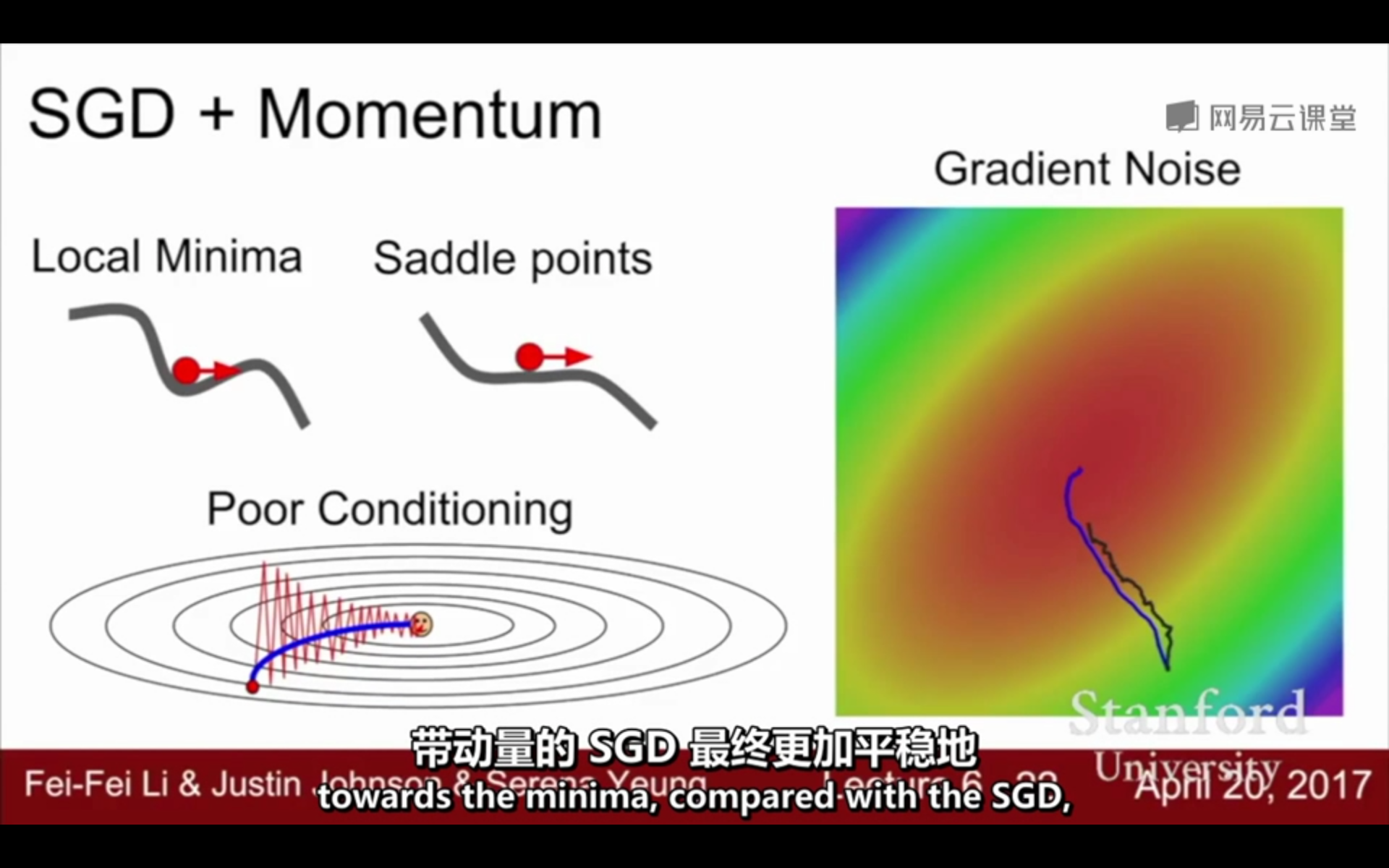
②容易陷入局部极小值和鞍点:
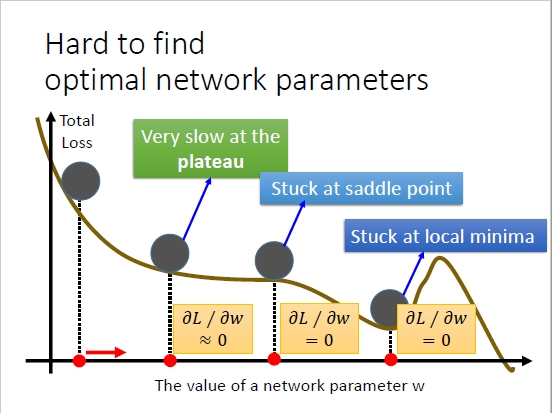

局部最小值:
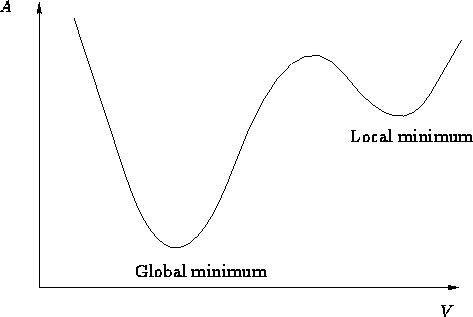
鞍点:
③对于凸优化而言,SGD不会收敛,只会在最优点附近跳来跳去 - 可以通过使用不固定的learning rate来解决
(凸优化的全局最优点是针对训练数据而言的,更换了当前训练数据,当前的最优点就变了。所以SGD本来就没有固定的全局最优点。最后得到的是多个batch上最优点的一个或几何均值)
2. SGD+Momentum(动量梯度下降):在SGD的基础上,引入一阶动量,增加惯性。SGD的缺点是参数更新方向只依赖于当前batch计算出的梯度,因此十分的不稳定。为了抑制SGD的震荡,可以在梯度下降的过程中加入惯性。t时刻的下降方向,不仅由当前点的梯度方向决定,还由此前的累积的梯度来决定。若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度
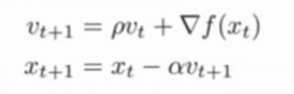
①一阶动量:是指到此刻为止的梯度的指数加权平均
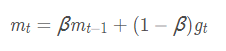
β的经验值一般为0.9:下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向,利用当前batch微调最终的更新方向。如果当前梯度方向与历史梯度一致,会增强该方向的梯度。如果不一致,能够减少更新
②指数加权平均(指数衰减平均):增加一个衰减系数来控制历史信息的获取多少,约等于1 /(1−β)个历史时刻的梯度向量和的平均值
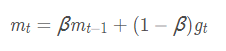

③利用momentum和当前梯度来更新位置(公式):下一个位置 = 当前位置 - 学习率*到此刻为止所积累的梯度 ;
到此刻为止所积累的梯度 = 动量因子*此前积累的梯度 +(1-动量因子)*此刻的梯度
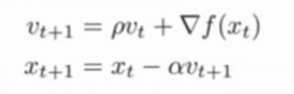
x_t+1:下一个位置 x_t:当前位置
v_t+1:当前积累的梯度 v_t:此前积累的梯度 ▽f(x_t):此刻的梯度
α:学习率 p:动量因子
④SDG和Momentum的区别:SGD每次都会在当前位置上沿着负梯度方向更新,并不考虑之前的方向梯度大小;而动量(moment)通过引入一个新的变量 v 去积累之前的梯度通过指数衰减平均得到v,达到加速学习过程的目的
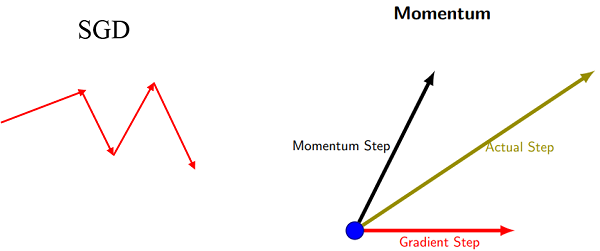
⑤优点:
- 增加了稳定性;
- 收敛速度更快;
- 具有一定摆脱局部最优的能力
因为下一个位置不仅取决于当前的梯度,还取决于之前积累的梯度,因此可以避免陷入局部最小值(梯度为0)和越过鞍点:
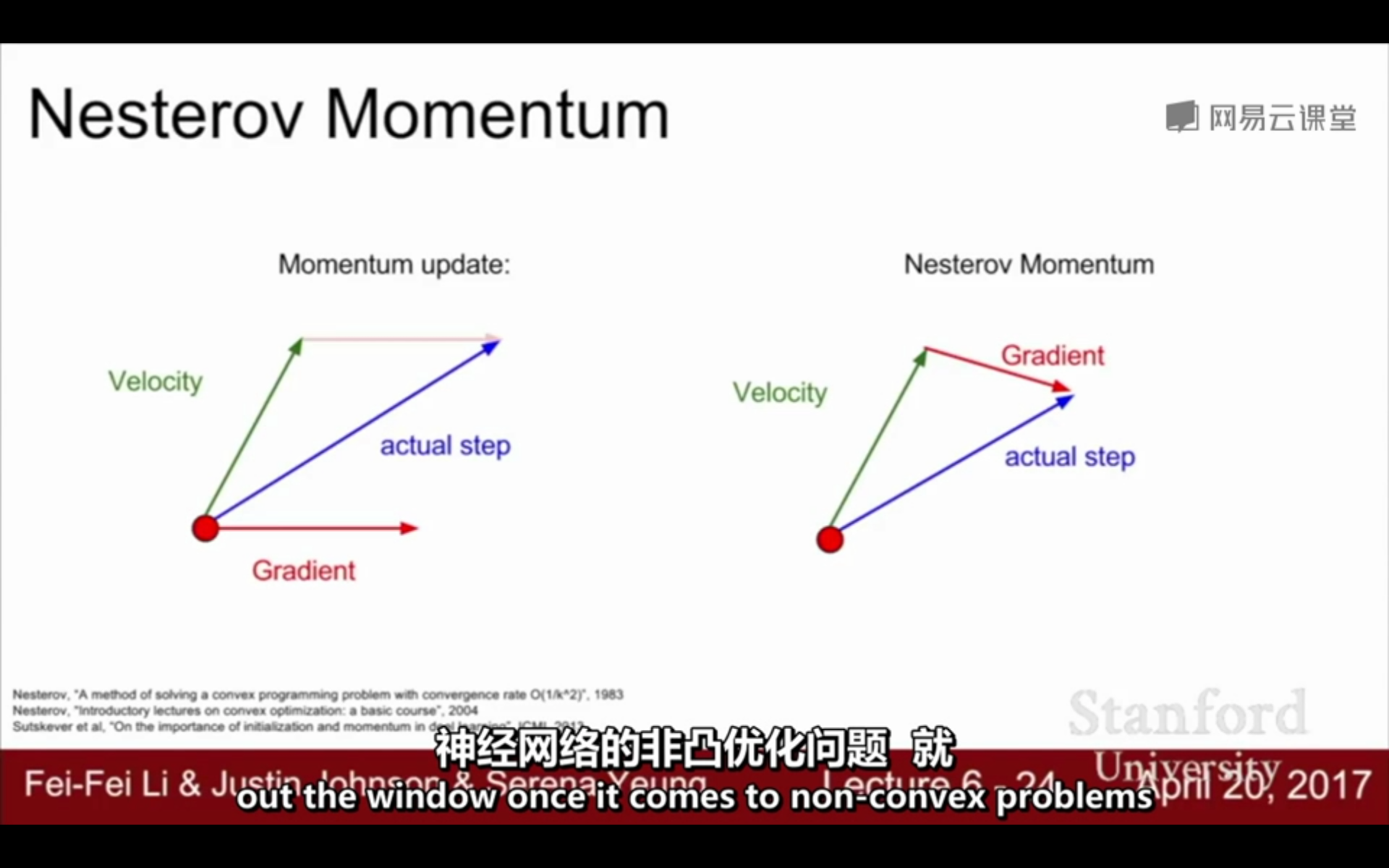
3. Nesterov Momentum(牛顿动量梯度下降):在Nesterov Momentum中,先沿着之前积累的梯度走一步,然后再计算这一步的终点的梯度,利用该梯度进行校正,得到最终的更新方向。相当于在Nesterov中添加了一个校正因子,Nesterov Momentum的位置更新取决于之前积累的梯度和根据之前积累梯度走到的位置的梯度

(不太明白这个公式)


Nesterov与Nesterov Momentum的区别:
在Nesterov中,t时刻的下降方向,不仅由当前点的梯度方向决定,还由此前的累积的梯度来决定;
在Nesterov Momentum中,t时刻的下降方向,取决于之前积累的梯度和根据之前积累梯度走到的位置的梯度
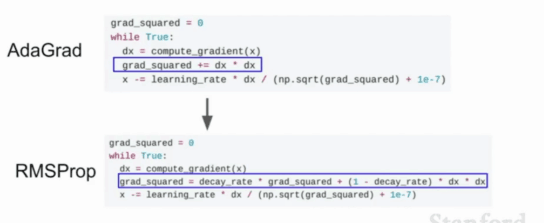
4. AdaGrad(Adaptive Gradient)自适应梯度下降:能够在训练中自动对learning rate进行调整;每一次更新参数时(一次迭代),不同的参数使用不同的学习率,对于出现频率较低的参数采用较大的α更新;对于出现频率较高的参数采用较小的α更新;在每轮训练中对每个参数θi的学习率进行更新,将每一个参数的每一次迭代的梯度取平方累加再开方,用学习率除以这个数;AdaGrad适合处理稀疏矩阵(为什么)
公式:
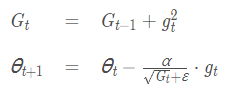
二阶动量:到此刻为止的梯度平方的累加(AdaGrad的二阶动量是到此刻为止的梯度平方的累加)

优点和缺点:

5. RMSProp(root mean square prop)均方根传播: 使用指数加权平均(指数衰减平均)只保留过去给定窗口大小的梯度,而非累加全部历史梯度。累加之前所有的梯度平方和容易造成梯度消失,所以RMSProp只关注过去一段时间窗口的下降梯度,避免了二阶动量持续累积,导致训练过程提前结束的问题
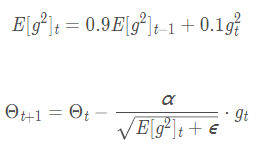
①二阶动量:到此刻为止的梯度的指数加权平均(RMSProp的二阶动量是到此刻为止的梯度的指数加权平均)
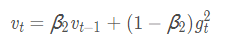
B常取0.9:
![]()
AdaGrad和RMSProp的区别:
6. Adam(Adaptive Moment Estimation)自适应矩估计:将Momentum和RMSprop结合在一起,引入一阶动量和二阶动量,利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率;经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳
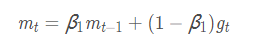
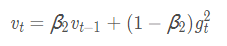
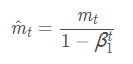
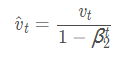
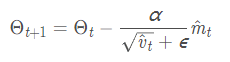
m_t:一阶动量 v_t:二阶动量
^m_t:一阶动量的校正 ^v_t:二阶动量的校正
θ_t+1:下一个位置 θ_t:当前位置
β1、β2:加权平均数,用于控制一阶动量和二阶动量

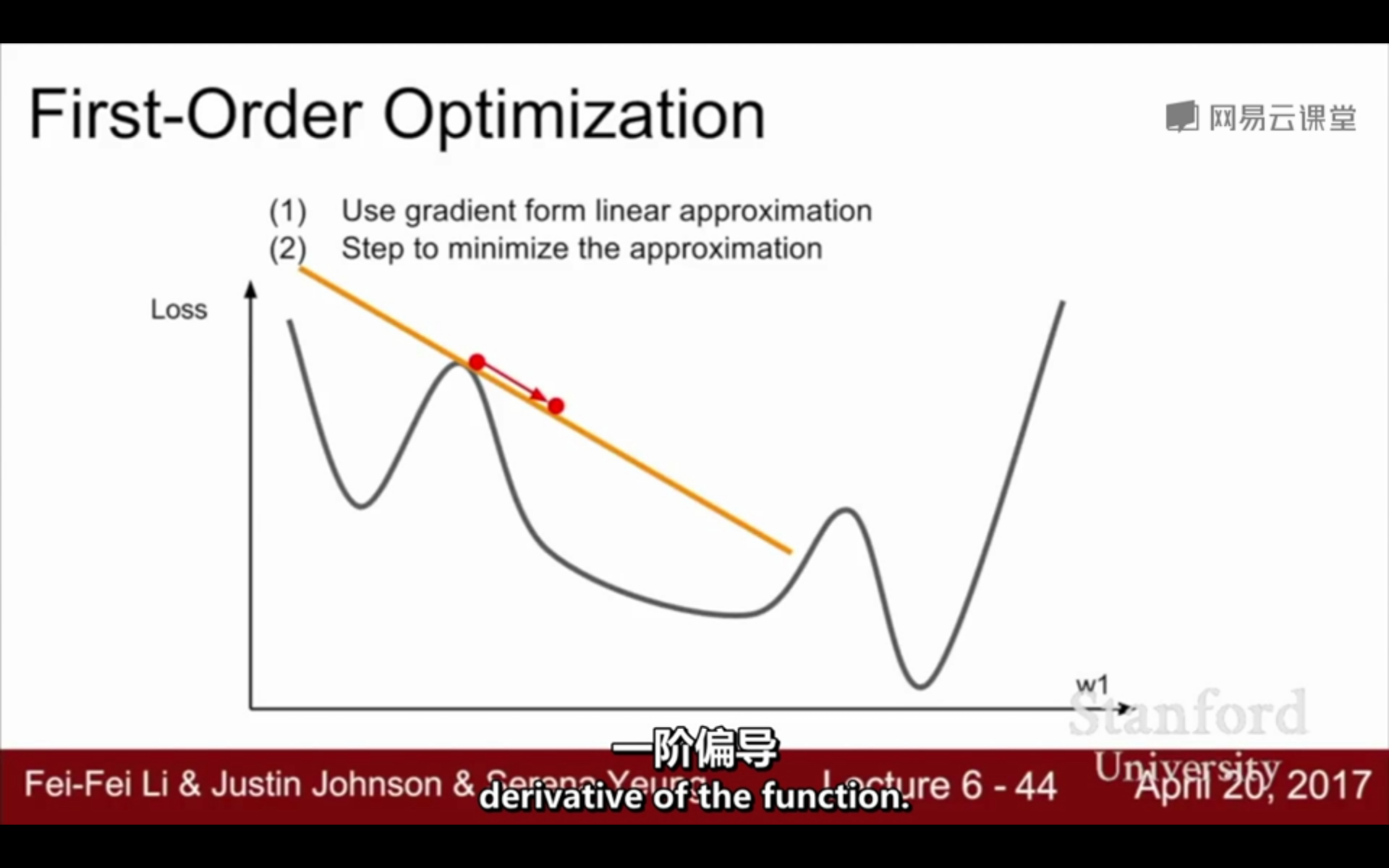
①一阶优化与二阶优化:
一阶优化:
(1)使用梯度形式的线性近似
(2)最小化近似的步骤
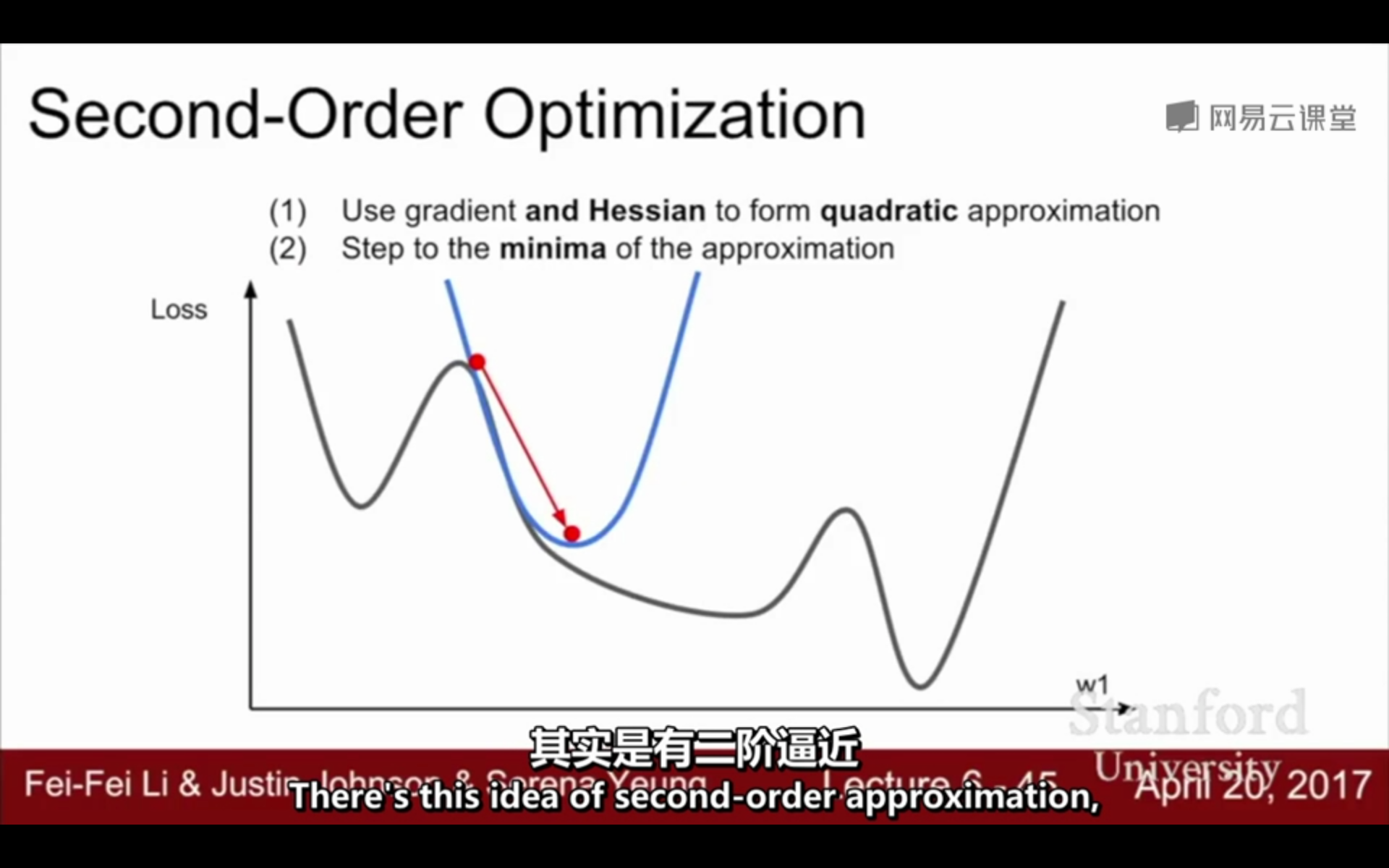
二阶优化:
(1)利用梯度和Hessian形成二次逼近
(2)逼近最小值的步骤

②目前实践中优先选择Adam:

参考:
https://blog.csdn.net/u012328159/article/details/80311892
https://blog.csdn.net/yinyu19950811/article/details/90476956
https://blog.csdn.net/u010089444/article/details/76725843


