ccf 201812-4

 

 

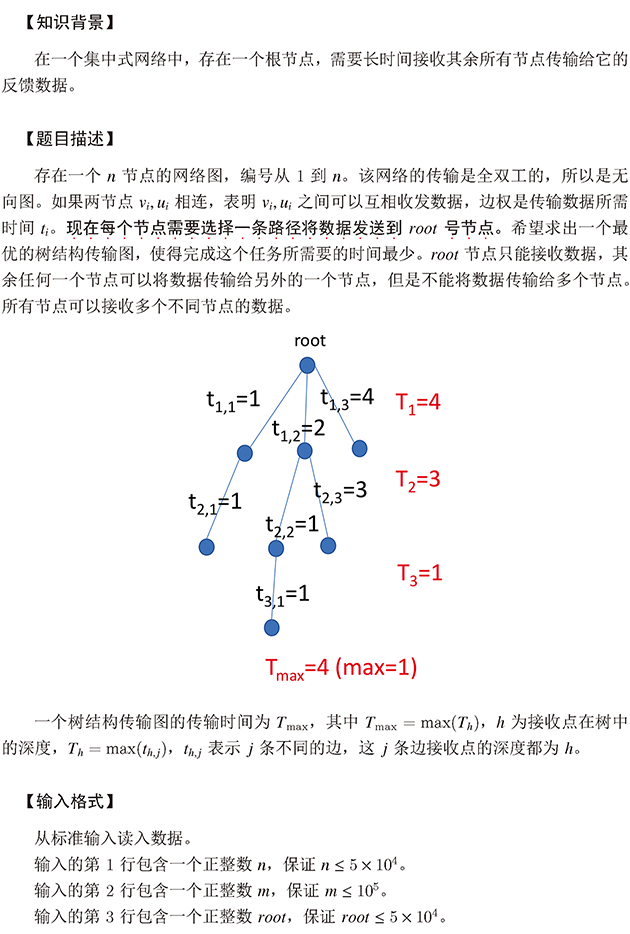
题解：求最小生成树的最大权值边

△prim是什么？Kruskal大法好！不会超时还不用优化 www

 

Kruskal解法：78ms

#include <stdio.h>
#include <algorithm>
#define MAX 50005
#define MAX_EDG 100005

using namespace std;

typedef struct Node{
    int u;
    int v;
    int w;
}Node;


Node map[MAX_EDG];
int father[MAX];    //自己的父亲 
int rank_[MAX];        //秩 

bool cmp(Node a, Node b){
    return a.w < b.w;    //从小到大 升序
}

int find(int x){
    if(father[x]==x)    return x;
    else return    father[x]=find(father[x]);        //向上找父亲直到找到根节点 
}

void unite(int x, int y){
    if(find(x) == find(y))    return;
    else{
        int x_root=find(x);
        int y_root=find(y);
        if(rank_[x_root] > rank_[y_root])            //按秩合并   //比较的是树根x_root和y_root的秩 ，不是x和y的 
            father[y_root]=x_root;
        else if(rank_[y_root] > rank_[x_root])
            father[x_root]=y_root;
        else{                            //两个树根的秩一样的话，任意合并到其中一个树根中，然后秩++ 
            father[x_root]=y_root;
            rank_[y_root]++;
        }    
    }
}

void init(int n){
    for(int i=1;i<=n;i++){
        father[i]=i;        //自己是自己的父亲 
        rank_[i]=0;            //初始高度为0 
    }
}

int main(){
    int n,m,root;
    int count,max_dis;
    int u,v,w;
    while(scanf("%d",&n)!=EOF){
        scanf("%d",&m);
        scanf("%d",&root);
        init(n);
        for(int i=1;i<=m;i++)
            scanf("%d %d %d",&map[i].u,&map[i].v,&map[i].w);
        sort(map+1, map+m+1, cmp);            //sort排序，由小到大 
        count=0;
        max_dis=0;
        for(int i=1;i<=m;i++){
            if(count==n-1)    break;
            u=map[i].u;
            v=map[i].v;
            w=map[i].w;
            if(find(u)!=find(v)){        //如果不在同一个子树就合并 
                unite(u,v);
                count++;
                if(w>max_dis)
                    max_dis=w;
            }
        }
        printf("%d\n",max_dis); 
    }
    return 0;
}

 

 

Prim解法：203ms  （不优化，超时。[ 留下不学无术的眼泪）

①n<=50000，用二维数组会编译出错，开不了50000*50000这么大的数组

②用Vector+优先队列 优化Prim即可得正解，一定要用优先队列优化，否则会超时！

③可以用struct Node，也可以用Pair优化

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <vector> 
#include <queue>
#define MAX 50005
#define INF 0x3f3f3f3f

using namespace std;

typedef struct Node{
    int v;　　　　//边的顶点
    int w;　　　　//权值
}Node;

struct cmp{                            //重载Node的比较运算符 
     bool operator()(Node a,Node b){
        return a.w>b.w;
    }
};

vector<Node> map[MAX];
priority_queue <Node, vector<Node>, cmp >q;            //用优先队列优化 
int vis[MAX];        //是否被访问过 
int dis[MAX];        //该集合到所有点的最短距离
int max_dis;        
int n,m;

void prim(){
    memset(dis,INF,sizeof(dis));
    memset(vis,0,sizeof(vis));
    dis[1]=0;
    max_dis;
    int min_,k;
    Node node1;
    node1.v=1;    node1.w=0;
    q.push(node1);
    while(!q.empty()){        //依次加入每一个顶点
        Node  node=q.top();
        q.pop();
        int v=node.v;
        int w=node.w;
        vis[v]=1;
        if(dis[v] > max_dis)
            max_dis=dis[v];
        for(int j=0;j<map[v].size();j++){            //更新与v点相邻的点v到集合V'的最短距离
            int v_=map[v][j].v;
            int w_=map[v][j].w;
            if(!vis[v_]){
                if(dis[v_]>w_){        //点v没有被访问过且点v到点k的距离小于点v到集合V'的距离
                    dis[v_]=w_;
                    Node node_;
                    node_.v=v_;        node_.w=w_;
                    q.push(node_);
                }
            }
        }
    }
} 

int main(){
    int root;
    int u,v,w;
    while(scanf("%d",&n)!=EOF){
        scanf("%d",&m);
        scanf("%d",&root);
        for(int i=1;i<=n;i++)
            map[i].clear();
        for(int i=0;i<m;i++){
            scanf("%d %d %d",&u,&v,&w);
            Node node1,node2;
            node1.v=v;    node1.w=w;
            map[u].push_back(node1);
            node2.v=u;    node2.w=w;
            map[v].push_back(node2);
        }
        prim();
        printf("%d\n",max_dis);
    }
    return 0;
}