10.24三题
10.24今日三题
CF645E Intellectual Inquiry
给定长度为\(m\)字符串,在字符串后添加\(n\)个字符,使新字符包含不同的子序列数尽量多,求最多的不同子序列数量
转移分两种情况
当前字符未出现
当前字符出现过
最后每次贪心选取\(last_i\)最小的字符,使减的最小,\(f_i\)最大
char s[N>>1]; int n,k,len,lst[200];ll f[N];
priority_queue<pair<ll,int> >q;
int main(){
scanf("%d%d",&n,&k);
scanf("%s",s + 1); len = strlen(s + 1);
for(int i = 1;i <= len;++i){
if(!lst[s[i]]) f[i] = (f[i-1] <<1|1) % mod;
else f[i] = ((f[i-1]<<1) - f[lst[s[i]]-1] + mod) % mod;
lst[s[i]] = i;
}
for(char i = 'a';i < 'a' + k;++i)
q.push(make_pair(-lst[i],i));
for(int i = 1;i <= n;++i){
int minn = -q.top().first;
int pos = q.top().second; q.pop();
int now = i + len;
if(!minn) f[now] = (f[now-1]<<1|1) % mod;
else{
f[now] = ((f[now-1]<<1) - f[minn-1] + mod) % mod;
}
lst[pos] = now;
q.push(make_pair(-now,pos));
}
ll ans = f[n + len] + 1;
printf("%lld",ans);
}
CF859E Desk Disorder
偷的\(HE\)轰态氧\(chpu437\)的图\(2333\)
\(2N\)个节点\(N\)个人,每个人位于节点上,每个人都有想去的节点(可以是当前点),一个人可以保持在当前点不动,也可以去想去的点,为保证不存在一个点上有超过一个人的方案数有多少种
根据题意,图中至多会存在一个出度为\(0\)的点,分类讨论
\(1.\)有一个这样的点
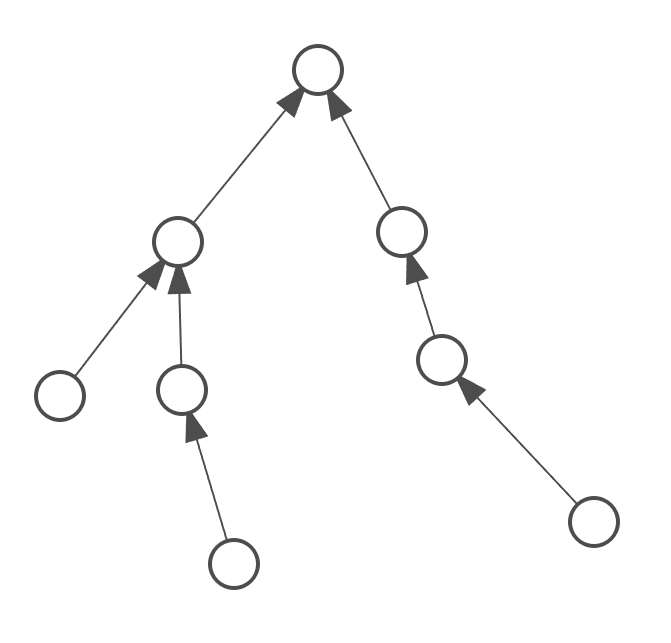
显然这玩意是个树,除去根,对于树上的节点,如果它要到达下一个节点,它指向节点这一路径所有点前进一步,每个点都有这样一个方案,方案为\(n-1\)种,所有点不动,有一种方案,总共\(n\)种方案
当树上有自环,你会发现只能有一种方案,所以要判一下
\(2.\)不存在这样的点
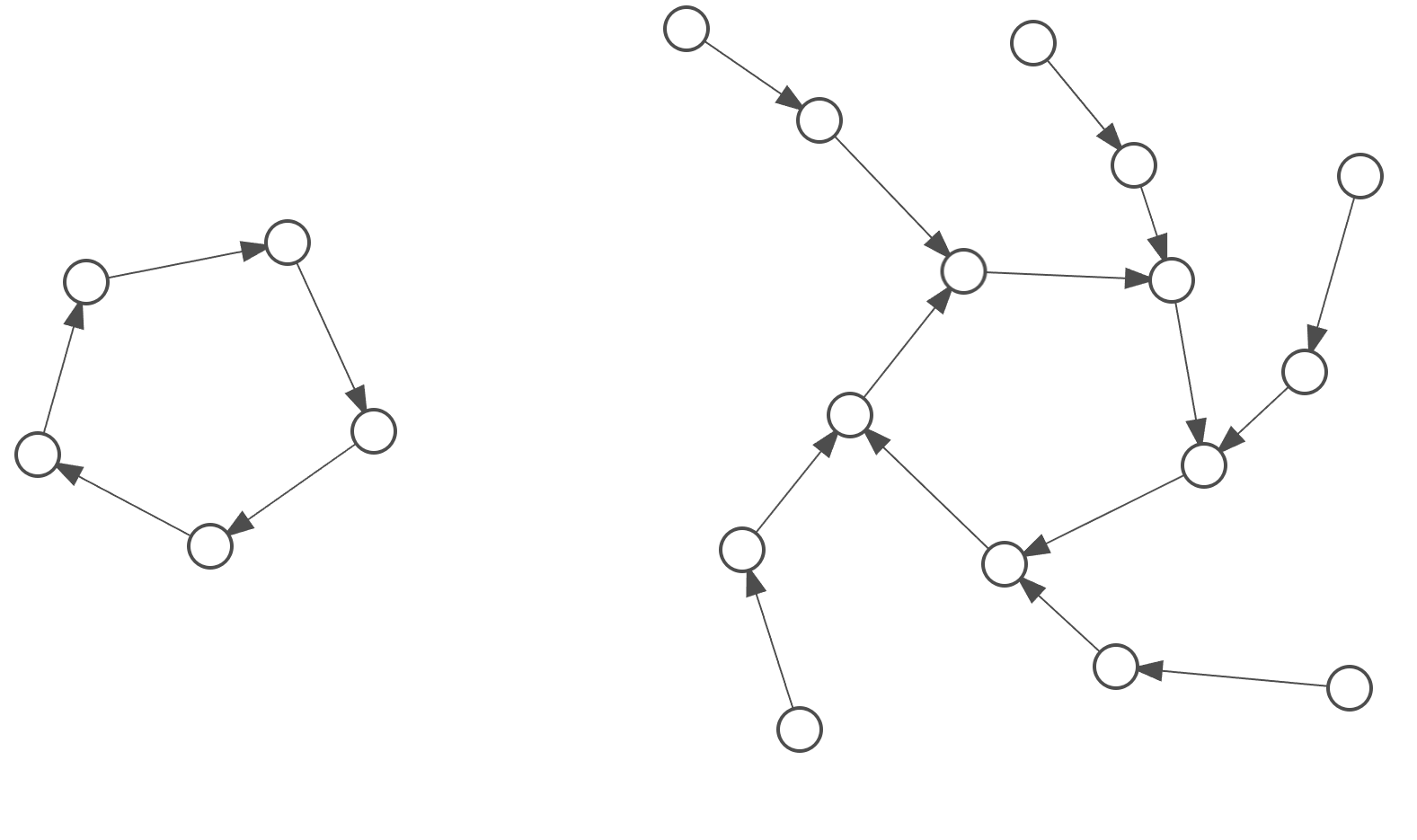
对于一个环,只有全部移动和全部不动,对于基环树,每个链不可动,所以方案数均为\(2\)
题目有自环,自环显然方案为\(1\),
用各路玄学判环即可:冰茶几,大法师,脱蒲排序(Orz大帝),
最后乘法原理一乘即可
int fa[N],siz[N]; bool deg[N],circle[N],selfcir[N];
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}
int main(){
int n;long long ans = 1; n = read();
for(int i = 1;i <= n<<1;++i){
fa[i] = i; siz[i] = 1;
} int u,v;
for(int i = 1;i <= n;++i){
u = read(); v = read(); deg[u] = true;
if(u == v){
selfcir[u] = true;
continue;
}
else{
u = find(u); v = find(v);
if(u == v && !selfcir[u]){
ans = (ans<<1) > mod ? (ans<<1) - mod : (ans<<1);
circle[u] = true; continue;
}
siz[v] += siz[u]; selfcir[v] |= selfcir[u];//判断树上自环
fa[u] = v;
}
}
for(int i = 1;i <= n<<1;++i){
if(!deg[i] && !selfcir[i])//如果树上有自环,相当于乘1
ans = (ans * siz[i]) % mod;
}
printf("%lld",ans);
}
P6822 [PA2012]Tax
给出一个\(n\)个点,\(m\)条边的无向图,经过一个点代价是进入和离开这个点的两条边的边权较大值,求\(1\)到\(n\)的最小代价,起点的代价是离开起点的边的边权,终点的代价是进入终点边的边权
权值收到两条边影响,考虑给边建边,在新图跑最短路
naive想法是\(a\to b\to c\)边设成\(\max(z1,z2)\),跑最短路,但是边数是\(m^2\)的
建立超级源点\(s\)和超级汇点\(t\),无向边拆成有向边,边转点,
对于所有从\(1\)出发的边,从\(s\)向这些边对应的点连权值为原图权值的边
枚举\(b\)点,把\(b\)的所有出边编号找出,然后按边权排序,把边编号直接做差相连,边数会变成\(m\)
跑最短路即可
# define pli std::pair<long long, int>
# define mkp std::make_pair
struct edge {
int v, next; long long w; int id;
const bool operator < (const edge that) const {
return this->w < that.w;
}
} e[MAXM<<1];
int hd[MAXM<<1], cntE;
long long dis[MAXM<<1];
bool vis[MAXM<<1];
std::vector<edge>vec[MAXN];
void AddE(int u, int v, long long w) {
e[++cntE] = (edge) {v, hd[u], w, 0};
hd[u] = cntE;
}
void Dij(int s, int t) {
memset(dis, 0x3f, sizeof(dis));
std::priority_queue<pli, std::vector<pli>, std::greater<pli> >H;
dis[s] = 0;
H.push(mkp(dis[s], s));
while(H.size()) {
int now = H.top().second;
H.pop();
if(!vis[now]) {
vis[now] = true;
for(int i = hd[now]; i; i = e[i].next) {
if(dis[e[i].v] > dis[now] + e[i].w) {
dis[e[i].v] = dis[now] + e[i].w;
H.push(mkp(dis[e[i].v], e[i].v));
}
}
}
}
}
int main() {
int n, m; scanf("%d%d", &n, &m); int s = 0, t = 1;
for(int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
vec[u].push_back((edge){v, 0, w, i<<1});
vec[v].push_back((edge){u, 0, w, i<<1|1});
}
for(int i = 1; i <= n; i++) {
if(vec[i].size()) {
std::sort(vec[i].begin(), vec[i].end());
for(int j = 0; j < vec[i].size(); j++) {
AddE(vec[i][j].id^1, vec[i][j].id, vec[i][j].w);
if(i == 1)
AddE(s, vec[i][j].id, vec[i][j].w);
if(vec[i][j].v == n)
AddE(vec[i][j].id, t, vec[i][j].w);
}
for(int j = 1; j < vec[i].size(); j++){
AddE(vec[i][j].id, vec[i][j-1].id, 0);
AddE(vec[i][j-1].id, vec[i][j].id, vec[i][j].w-vec[i][j-1].w);
}
}
}
Dij(s, t);
printf("%lld", dis[t]);
return 0;
}


