向量叉积
向量叉积
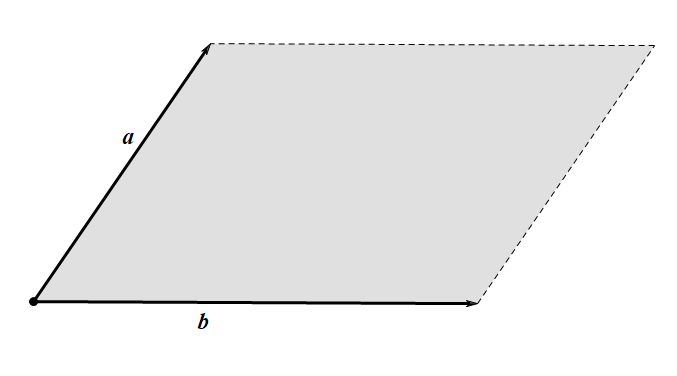
向量\(\vec{a}\times\vec{b}\)表示这个四边形的面积
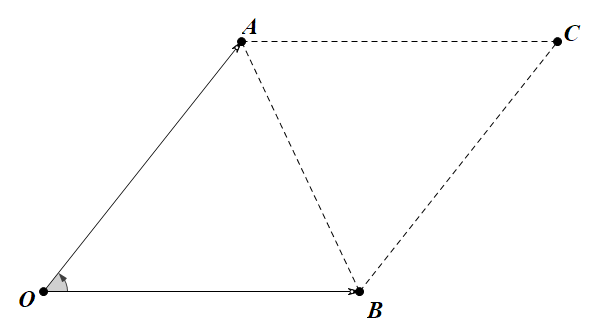
可知三角形\(OAB\)面积为\(S_{平行四边形}/2=|\vec{a}|*|\vec{b}|\sin AOE=|\vec a\times\vec b|\)
结论:设向量\(\vec a=(x_1,y_1),\vec b=(x_2,y_2)\) 向量叉积为\(x_1y_2-x_2y_1\)
由叉积定义\(\vec a\times\vec b=|\vec{a}|*|\vec{b}|\sin<\vec a,\vec b>\)
\[=\sqrt{(|\vec a|*|\vec b|)^2-(|\vec a·\vec b|)^2}\\
=\sqrt{x_1^2y_2^2+x_2^2y_1^2-2x_1x_2y_1y_2}\\
=\sqrt{(x_1y_2-x_2y_1)^2}=|x_1y_2-x_2y_1|
\]
判断正负号可得\(\vec a\times\vec b=x_1y_2-x_2y_1\)
转载了部分


