曼哈顿距离和切比雪夫距离转化

曼哈顿距离和切比雪夫距离

两个点的距离定义为点 \((x,y)\) 和它周围的\(8\)个点
\((x-1,y)(x+1,y),(x,y-1),(x,y+1),(x-1,y+1),(x-1,y-1),(x+1,y+1),(x+1,y-1)\)距离为\(1\)

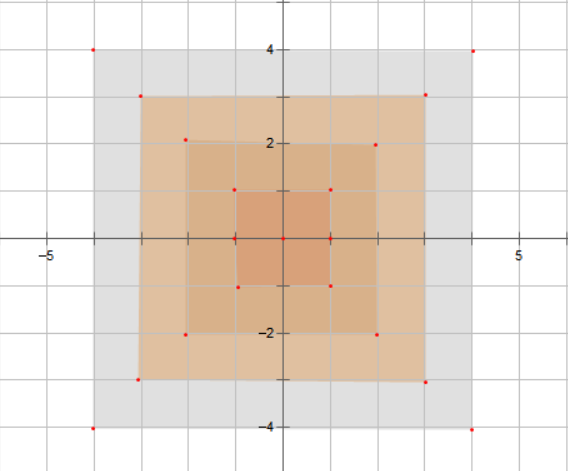
(用下\(gyx\)学长的图)

切比雪夫距离\(dis=\max(\Delta X,\Delta Y)\) \(\Delta X\)为两个点距离横坐标差绝对值

将\((x,y)\)坐标变为\((x+y,x-y)\)后，原坐标系曼哈顿距离\(=\)新坐标系切比雪夫距离

曼哈顿距离\(|x_1-x_2|+|y_1-y_2|\)，可以表示成

\[max\{x_1-x_2+y_1-y_2,x_1-x_2+y_2-y_1,x_2-x_1+y_1-y_2,x_2-x_1+x_2-y_1\} \]

考虑变\((x1,y1),(x2,y2)\) 为 \((x1+y1,x1-y1)(x2+y2,y2-y2)\)

切比雪夫距离为\(\max\{|(x_1+y_1)-(x_2+y_2)|,|(x_1-y_1)-(x_2-y_2)|\}\)

两点曼哈顿距离加绝对值可表示为上面的切比雪夫距离

将\((x,y)\)坐标变为\(\large(\frac{x+y}2,\frac{x-y}2)\)后，原坐标切比雪夫距离\(=\)新坐标曼哈顿距离

P3964 TJOI2013 松鼠聚会

给你\(n\)个点，选一个点使这个点到其他点切比雪夫距离之和最小

枚举每个距离匹配，暴力是\(n^2\)的

把切比雪夫距离转换成曼哈顿距离，横纵坐标分开求，只写横坐标了，另一个同理

令坐标有序

\[\Delta X(1,i)+\Delta X(2,i)+...\Delta X(n,i)\\ =|X_i-X_1|+|X_i-X_2|...+|X_i-X_n|\\ =(X_i-X_1)+...+(X_i-X_i)+(X_{i+1}-X_i)+...+(X_n-X_i)\\ =(i*X_i-\sum_{k=1}^iX_k)+(\sum_{k=i+1}^nX_k-(n-i)*X_i)\\ \]

前缀和优化

const ull MAX = 0x7777777777777f;
int n,x[N],y[N],gx[N],gy[N];
ull sumx[N],sumy[N];
inline ull calc(int i){
	int rx = lower_bound(gx + 1,gx + n + 1,x[i]) - gx;
	int ry = lower_bound(gy + 1,gy + n + 1,y[i]) - gy;
	return rx * 1LL * x[i] - sumx[rx] + sumx[n] - sumx[rx] - (n - rx) * 1LL * x[i] +
    ry * 1LL * y[i] - sumy[ry] + sumy[n] - sumy[ry] - (n - ry) * 1LL * y[i];
}
int main(){
	scanf("%d",&n);int xi,yi;
	for(int i = 1;i <= n;++i){
		scanf("%d%d",&xi,&yi);
		x[i] = gx[i] = xi + yi;
		y[i] = gy[i] = xi - yi;
	}
	sort(gx + 1,gx + n + 1);
	for(int i = 1;i <= n;++i)
		sumx[i] = sumx[i-1] + gx[i];
	sort(gy + 1,gy + n + 1);
	for(int i = 1;i <= n;++i)
		sumy[i] = sumy[i-1] + gy[i];
	ull res = MAX;
	for(int i = 1;i <= n;++i)
		res = std::min(res,calc(i));
	printf("%llu",res >> 1LL);
}

\(MAX\)能开多大开多大，建议开ULL_MAX