bzoj4173 数学

还是爆炸欧鸡的题难qwq

\[φ(n)*φ(m)*\sum_{k\in S(n,m)}φ(k)~mod~p,p=998244353且S(n,m)=\{n~mod~k+m~mod~k\ge~k\}\\ 打表都找出规律了555,写龟速乘写挂了,抱灵了,要不然就rank1了100pts->0\\ 因为n~\%~k=n-\lfloor \frac nk\rfloor*k\\ S(n,m)等价于\lfloor\frac{n+m}{k}\rfloor-\lfloor\frac nk\rfloor-\lfloor\frac mk\rfloor=1\\ \sumφ(k)[n\%k+m\%k\ge k]=\sumφ(k)[\lfloor\frac{n+m}{k}\rfloor-\lfloor\frac nk\rfloor-\lfloor\frac mk\rfloor=1]\\ 因为0\le\lfloor\frac{n+m}{k}\rfloor-(\lfloor\frac nk\rfloor+\lfloor\frac mk\rfloor)<2\\ 所以上式可以化成\sum_{k=1}^{n+m}φ(k)(\lfloor\frac{n+m}{k}\rfloor-\lfloor\frac nk\rfloor-\lfloor\frac mk\rfloor)\\ =\sum_{i=1}^{n+m}φ(k)\lfloor\frac{n+m}{k}\rfloor-\sum_{k=1}^n\lfloor\frac nk\rfloorφ(k)-\sum_{k=1}^m\lfloor\frac mk\rfloorφ(k),这里开始没搞懂,因为枚举超过n和m时就取0了\\ \sum_{k=1}^nφ(k)*\lfloor\frac nk\rfloor咋搞?通过\sum_{k|n}φ(k)=n \\ \sum_{k=1}^nφ(k)*\lfloor\frac nk\rfloor=\sum_{i=1}^n\sum_{k|i}φ(k)=\sum_{i=1}^ni\\ [1,n]中约数有k的个数是\lfloor\frac nk\rfloor\\ 然后等差求和了原式就为φ(m)*φ(n)*mn \]

#include<bits/stdc++.h>
#define mod 998244353
using namespace std;
typedef long long ll;
const int inf =0x3f3f3f3f;
const double eps=1e-8;
ll read()
{
    ll res=0,f=1;
    char ch=getchar();
    while(ch<'1'||ch>'9'){f=ch=='-'?-1:1;ch=getchar();}
    while(ch>'1'&&ch<'9'){res=res*10+ch-'0';ch=getchar();}
    return res*f;
}
ll n,m;
ll phi(ll n)
{
    ll i,re=n;
    for(i=2;i*i<=n;i++){
        if(n%i==0){
            re=re/i*(i-1);
            while(n%i==0){n/=i;}
        }
    }
    if(n!=1){re=re/n*(n-1);}
    return re;
}
int main()
{
    scanf("%lld%lld",&n,&m);
    printf("%lld\n",phi(n)%mod*(phi(m)%mod)%mod*(n%mod)%mod*(m%mod)%mod);
    return 0;
}

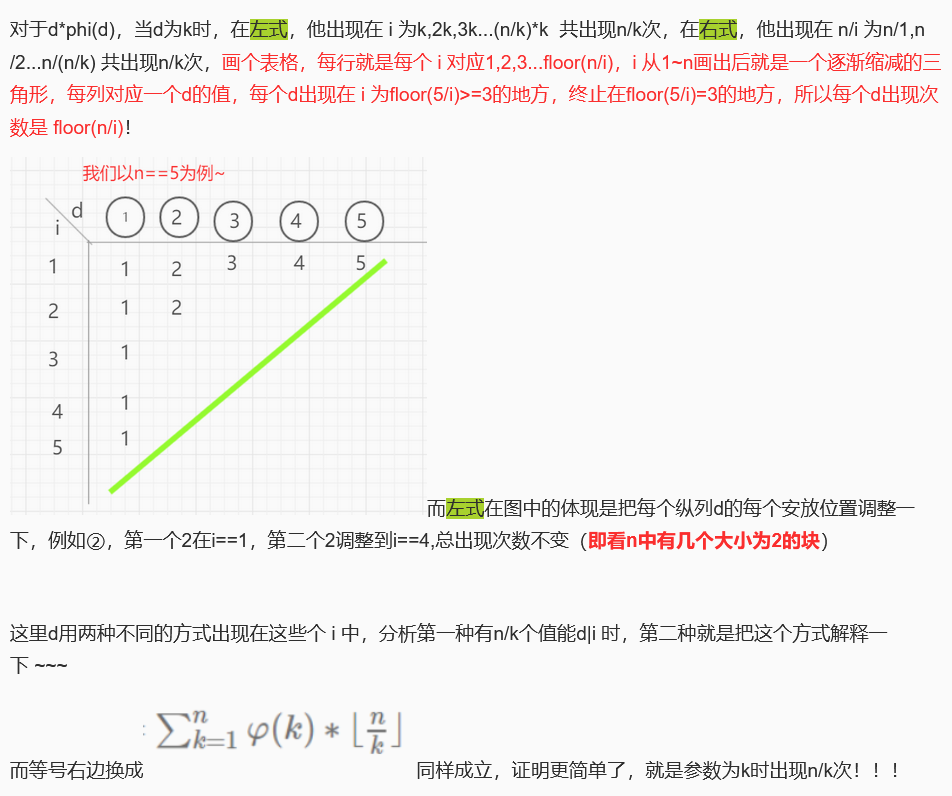
上图是windfreedom大佬的博客截下来的 写下出处

这题不用龟速乘qwq