矩阵系列

矩阵加法：

一般是同型矩阵（即行列一样的）相加和 每个位置相加

减法：

与加法类似

矩阵数乘：

矩阵乘常数

矩阵乘矩阵：

在向量乘向量的运算中，是将每个元素与它对应的元素相乘，求所有乘积之和

例子：A为n*k矩阵，B为k*m矩阵，C为m*n，A和B可乘，B和C可乘,C和A可乘

//注意左乘和右乘不一样

A和B,那么它们的乘积C则为一个n∗m矩阵

 

 

 

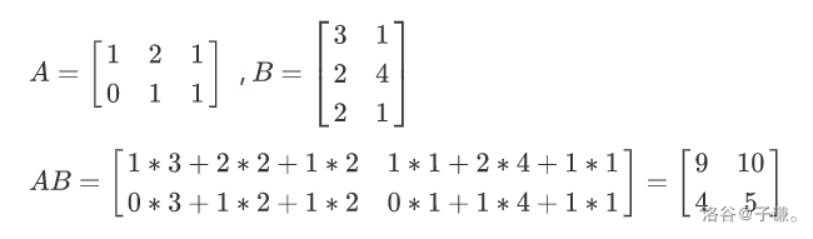
//大佬的图qwq

矩阵乘法满足交换结合

在普通的乘法中，一个数乘1还是等于它本身，在矩阵乘法中也有这么一个“1”，它就是单位矩阵

不同于普通乘法中的单位1，对于不同矩阵他们的单位矩阵大小是不同的

对于n∗m的矩阵，它的单位矩阵大小为m∗m，对于m∗n的矩阵，它的单位矩阵大小为n∗n

也就是说单位矩阵都是正方形的，这是因为只有正方形的矩阵能保证结果和前一个矩阵形状相同

单位矩阵的元素非0即1，从左上角到右下角的对角线上元素皆为1，其他皆为0

 

 

 

 

 

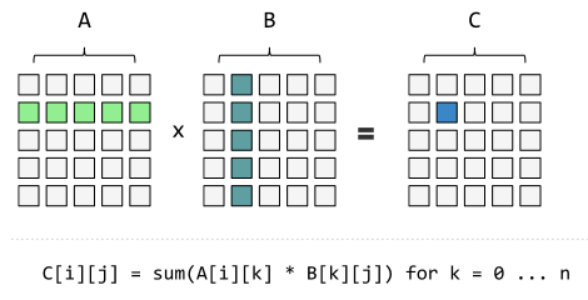
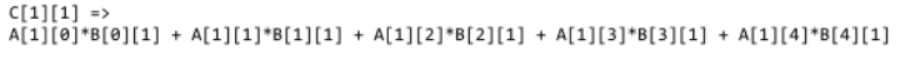
矩阵乘法加速递推

F是1*n的矩阵，A是n*n的矩阵F’=F*A也是1*n的矩阵

F和F’可用一维数组

省略行下标i

 

 

 

 

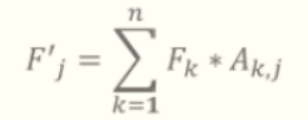
洛谷板子

 

 

#include<cstdio>
#include<cstring>
#define maxn 101
#define mod 1000000007
using namespace std;
typedef long long ll;
ll n,k;
inline ll read()
{
    ll x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
struct az{
    ll a[maxn][maxn];
    az(){
        memset(a,0,sizeof a);
    }
    inline void build(){     //建造单位矩阵
        for(int i=1;i<=n;++i)a[i][i]=1ll;
    }
}a;
az operator *(const az &x,const az &y){
    az z;
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)    
            z.a[i][j]=(z.a[i][j]+x.a[i][k]*y.a[k][j]%mod)%mod;
    return z;
}

int main()
{
    n=read(); k=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            a.a[i][j]=read();
    az ans;ans.build();
    while(k){
        if(k&1)ans=ans*a;
        a=a*a;k>>=1;
    }
    for(int i=1;i<=n;putchar('\n'),++i)
        for(int j=1;j<=n;++j)
            printf("%d ",ans.a[i][j]);
    return 0;
}