二、机器学习模型评估

二、机器学习模型评估

2.1 模型评估：基本概念

• 错误率(Error Rate)

  • 预测错误的样本数a占样本总数的比例m

\[E=\frac{a}{m} \]

• 准确率(Accuracy)

  准确率=1-错误率准确率=1−错误率

• 误差(Error)

  • 学习器的实际预测输出与样本的真实输出之间的差异

• 训练误差(Training Error)或经验误差(Empirical Error)

  • 学习器在训练集上的误差

• 泛化误差(Generalization Error)

  • 学习器在新样本上的误差

• 解释与泛化

  • 当模型在训练集上表现很好而在新样本上误差很大时，称为过拟合；反之模型在训练集上误差就很大时，称为 欠拟合。

• 过拟合和欠拟合

2.2 判别方法

判别方法：误差

引起误差的原因主要是因为偏差和方差。

• 偏差(Bias)
  • 描述的是预测值（估计值）的期望与真实值之间的偏离程度。偏差越大，越偏离真实数据。
• 方差(Variance)
  • 描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散。
• 偏差和方差对误差Error的影响可以表示为

\[Error = Bias + Variance + Noise \]

• 偏差（bias）造成的误差 - 准确率和欠拟合
  如果模型具有足够的数据，但因不够复杂而无法捕捉基本关系，即如果模型不适当，则会出现偏差。这样一来，模型一直会系统地错误表示数据，从而导致预测准确率降低出现欠拟合。
• 方差（variance）造成的误差 - 精确率和过拟合
  方差就是指模型过于贴近训练数据，以至于没办法把它的结果泛化。而泛化正是机器学习要解决的问题，如果一个模型只能对一组特定的数据有效，换了数据就无效了，我们就说这个模型过拟合。

判别方法：学习曲线

2.3 解决方法

• 欠拟合通常容易解决
  • 如 增加数据、增大训练次数、增大学习率 或 使用更复杂的模型 等。
• 过拟合则很难解决
  • 常用的方法包括 简化模型，减少特征，更多的数据，交叉验证，正则化，Dropout 和 Shuffling 等。

当心陷阱：维度灾难(Curse of Dimensionality)

当维数提高时，模型空间的体积提高太快，因而可用数据变得很稀疏。
在高维空间中，所有的数据都很稀疏，从很多角度看都不相似，因而平常使用的数据组织策略变得极其低效。
为了获得在统计学上正确并且有可靠的结果，用来支撑这一结果所需要的数据量通常随着维数的提高而呈指数级增长。

如何避免维度灾难

实际上并没有一种固定的方法避免维度灾难，解决方法需要结合数据集和所选的模型。训练数据集越小，则用到的特征应当越少。

另外，对于诸如神经网络、kNN、决策树等泛化不好容易过拟合的分类器，维度应当适当的减少。而对于朴素贝叶斯和线性分类器等不太复杂的分类器，特征可以适当的增大。

2.4 数据集拆分

为了得到泛化误差小的模型，并避免过拟合，在构建机器模型时，通常将数据集拆分为相互独立的训练数据集、验证数据集和测试数据集

• 训练数据集(Train Dataset)用来构建机器学习模型
• 验证数据集(Validation Dataset)辅助构建模型，用于在构建过程中评估模型，为模型提供无偏估计，进而调整模型超参数
• 测试数据集(Test Dataset)用来评估训练好的最终模型的性能

为了划分这几种数据集，可以选择采用留出法、K-折交叉验证法或者自助法等多种方法。这些方法都对数据集有一些基本的假设，包括：

• 数据集是随机抽取且独立同分布的
• 分布是平稳的，不会随时间发生变化
• 始终从同一个分布中抽取样本

陷阱：请勿对测试数据集进行训练。

自助法的性能评估变化小，在数据集小、难以有效划分数据集时很有用。另外，自助法也可以从初始数据中产生多个不同的训练集，对集成学习等方法有好处。

然而，自助法产生的数据集改变了初始数据的分布，会引入估计偏差。因而，数据量足够时，建议使用留出法和交叉验证法。

数据集拆分：留出法

留出法（hold-out）直接将数据集划分为互斥的集合，如通常选择 80% 数据作为训练集，20% 作为测试集。

需要注意的是保持划分后集合数据分布的一致性，避免划分过程中引入额外的偏差而对最终结果产生影响。

通常来说，单次使用留出法得到的结果往往不够稳定可靠，一般采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。

数据集拆分：K-折交叉检验法

机器学习中，算法模型性能比较是比较复杂的。

• 我们希望比较的是泛化性能，而实际中只能得到测试集上的性能，两者的结果未必相同
• 测试集上的性能跟测试集本身的选择有很大关系
• 很多机器学习算法本身有一定的随机性，即便用相同参数运行在同一个测试集上，多次的运行的结果也有可能不同

数据集拆分：K-折交叉检验法

初始采样分割成K个子样本，一个单独的子样本被保留作为验证模型的数据，其他K-1个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果或者使用其它结合方式，最终得到一个单一估测。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次。方差Variance随着k的增大而减小。

K常常取10，所以又称为十折交叉检验。

参数调节

• 参数调节
  • 简称调参（parameter tuning），在进行模型评估与选择时，除了要对适用学习算法进行选择，还需对算法参数进行设定的过程称参数调节；
• 常用方法
  • 对每个参数选定一个范围和变化步长，例如在[0,0.2][0,0.2]范围内以0.05为步长，则实际要评估的候选参数值有5个，最终是从这5个候选值中产生选定值。

网格搜索

网格搜索法是指定参数值的一种穷举搜索方法，通过将估计函数的参数通过交叉验证的方法进行优化来得到最优的学习算法。

即将各个参数可能的取值进行排列组合，列出所有可能的组合结果生成参数网格。

然后将各组合用于训练，并使用交叉验证对表现进行评估。

在拟合函数尝试了所有的参数组合后，返回一个合适的分类器，自动调整至最佳参数组合，可以获得参数值

对SVM的C参数和gamma的网格搜索可视化结果如上图所示，可知{C=1.0，gamma = 0.1}时效果最好。

2.5 模型评价

• 分类模型
• 回归模型
• 聚类模型

模型评价：分类模型评价

• 分类模型是通过训练数据建立预测模型，并利用模型将需要预测的数据样本划分到已知的几个类别中的过程。
• 机器学习中常见分类算法：逻辑回归、决策树、朴素贝叶斯等

分类模型评价：混淆矩阵

• 标签
  • 在分类问题中，每一个样本都存在两种角度的标签: 一个是样本真实的标签，一个是模型预测的标签。
• 混淆矩阵
  • 根据每一个样本的两种角度的标签，可以得到一个混淆矩阵（Confusion Matrix）。混淆矩阵中的每一列代表预测类别 ，每一列的总数表示预测为该类别的样本的数目。每一行代表了样本的真实归属类别 ，每一行的数据总数表示该类别的样本的数目。

分类模型的评价指标主要基于混淆矩阵。对于二分类问题，每一个样本都可以划分到以下四种类型中：

• 真正(True Positive , TP)：样本真实类别是正向的，模型预测的类别也是正向的
• 真负(True Negative , TN)：样本真实类别是负向的，模型预测的类别也是负向的
• 假正(False Positive , FP)：样本真实类别是负向的，模型预测的类别是正向的（取伪）
• 假负(False Negative , FN)：样本真实类别是正向的，模型预测的类别是负向的（去真）

分类模型评价：多分类混淆矩阵

分类模型评价：评价指标

• 准确率(Accuracy)
• 精确率(Precision)
• 召回率(Recall)
• F1值(F1 score)
• ROC和AUC

1. 分类模型评价指标：准确率

在分类问题中最常见的指标是准确率(accuracy)，它表示模型预测正确的样本比例，即将正的判定为正，负的判定为负。

准确率的定义如下：

\[accuracy=\frac{TP+TN}{TN+FN+FP+TP} \]

在不均衡数据中，准确率无法很好地度量模型的好坏。

例如在文本情感分类数据集中，正面的样本占比为80%，负面的内容占比只有20%。

如果一个分类模型将所有的样本都预测为正面，这个模型显然是一个无用的模型，但是它的准确率却可以达到80%。

对于不均衡数据，精确率和召回率是比准确率更好的性能评价指标。

总样本量：100

\[accuracy=\frac { TP+TN }{ TN+FN+FP+TP } =\frac { 80+0 }{ 0+0+20+80 } =80 \]

1. 分类模型评价指标：精确率

精确率(precision)又称查准率，是指正确预测的正样本占所有预测为正样本的比例。

\[precision=\frac{TP}{TP+FP} \]

1. 分类模型评价指标：召回率

召回率(recall)又称查全率、灵敏度和命中率，是指样本中被正确预测的样本比例。

\[recall=\frac{TP}{TP+FN} \]

1. 分类模型评价指标：$$F_{\beta}$$值

单独考虑精确率和召回率是片面的，而F值则是一个综合考虑精确率和召回率的指标。

\[F_{\beta}=\frac{(1+\beta^2)precision\times recall}{\beta^2\times precision+ recall} \]

其中β为正数，其作用是调整精确率和召回率的权重。β越大，召回率的权重更大；β越小，则精确率的权重更大。当1β=1时，精确率和召回率的权重一样，此时称为F_1F1值，它是精确率和召回率的调和平均数。

1. 分类模型评价指标：假正率

假正率(False Positive Rate)为被预测为正的负样本结果数除以负样本实际数的比值。

假正率的定义为

\[FPR=\frac{FP}{FP+TN} \]

1. 分类模型评价指标：ROC曲线

ROC曲线通过召回率(TPR)和假正率(FPR)两个指标进行绘制图形，是一个画在ROC空间的曲线，横坐标为FPR， 纵坐标为TPR。

• (TPR=0,FPR=0)
  • 把每个实例都预测为负类的模型
• (TPR=1,FPR=1)
  • 把每个实例都预测为正类的模型
• (TPR=1,FPR=0)
  • 理想模型

一个好的分类模型应该尽可能靠近图形的左上角，而一个随机猜测模型应位于连接点(TPR=0,FPR=0)和(TPR=1,FPR=1)的主对角线上。

1. 分类模型评价指标：AUC

AUC就是处于ROC曲线下方的那部分面积的大小。通常AUC介于0.5到1.0之间，较大的AUC代表了较好的模型性能。

• 如果模型是完美的，那么它的 AUC=1AUC=1
• 如果模型是个简单的随机猜测模型，那么它的 AUG=0.5AUG=0.5
• 如果一个模型好于另一个，则它的曲线下方面积相对较大。
• 一般来说，AUC大于0.75可以认为是一个比较理想的模型。

分类模型评价指标：应用场景

• 如果需要你使用机器学习进行地震预报，您会选择哪个指标作为算法模型的评价指标？
• 如果需要你使用机器学习认定犯罪嫌疑人，您会选择哪个指标作为算法模型的评价指标？

回归模型评价指标

回归模型的预测值一般都是连续的。评价模型的指标没有统一的标准。下面介绍三个常用的方法：

• 平均绝对误差
• 均方误差
• 决定系数R^2R2

回归模型评价指标：平均绝对误差

平均绝对误差(Mean Absolute Error，MAE)是所有单个观测值与算术平均值的偏差的绝对值的平均。

\[MAE=\frac{1}{n}\sum_{i=1}^n|\hat{y_i}-y_i| \]

回归模型评价指标：均方误差

均方误差(Mean Squared Error，MSE)是衡量"平均误差"的一种较方便的方法，可以评价数据的变化程度。
均方根误差(Root Mean Square Error，RMSE)是均方误差的算术平方根，有时也用RMSE对回归模型进行评价。

\[MSE=\frac{1}{n}\sum_{i=1}^n(\hat{y_i}-y_i)^2 \]

回归模型评价指标：决定系数

在统计学中，通常使用决定系数对回归模型进行评价。假设样本真实值的平均值为：

\[y=\frac{1}{n}\sum_{i=1}^n \]

• 残差平方和为

\[SSE=\sum_{i=1}^n(y_i-\hat{y_i})^2 \]

• 总平方和为

\[SST=\sum_{i=1}^n(y_i-\bar{y_i})^2 \]

R^2R2的计算公式为

\[R^2(y,\hat{y})=1-\frac{SSE}{SST} \]

• 通常R^2R2取值范围为[0,1][0,1]
• R^2R2越趋近于1，说明回归效果越好。
• R^2R2越趋近于0，说明回归效果越差。

在一些回归效果非常差的情况下，残差平方和可能大于总平方和，此时可能小于0。

决定系数计算例子(重庆2017链家房价预测)

聚类模型评价指标

聚类模型的性能指标主要分为内部指标(Internal Index)和外部指标(External Index)两类。

• 内部指标适用于无标注数据，根据聚类结果中簇内相似度和簇间分离度进行聚类质量评估；
• 外部指标适用于有标注数据，将聚类结果与已知类标签进行比较。
• 内部指标
  • DB 指数
  • 轮廓系数
• 外部指标
  • Rand指数
  • 调整Rand指数

聚类模型评价：DB指数

聚类模型的目标是使得簇内数据尽量相似，不同簇之间的数据尽量不相似。

DB指数正是基于这个思想所构建的指标，它表示簇内距离与簇内距离与簇间距离之比，DB的值越小说明聚类效果越好。

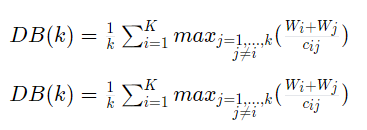
其中，K是聚类数目，W_i表示类C_i中的所有样本到其聚类中心的平均距离，W_j表示类C_i中的所有样本到类C_j中心的平均距离，Cij表示类C_i和C_j中心之间的距离。

DB越小表示类与类之间的相似度越低，从而对应越佳的聚类结果。

聚类模型评价：轮廓系数

轮廓系数结合了内聚度和**分离度两种因素，可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。对于样本ii的轮廓系数其计算公式：

\[s(i)=\frac{b(i)-a(i)}{max(a(i),b(i))} \]

• a(i)=average(样本i到所有它属于的簇中其它点的距离)a(i)=average(样本i到所有它属于的簇中其它点的距离)，表示ii向量到同一簇内其他点不相似程度的平均值；
• b(i)=min(样本i到所有非本身所在簇的点的平均距离)b(i)=min(样本i到所有非本身所在簇的点的平均距离)，表示样本ii到其他簇的平均不相似程度的最小值。

\[s(i)=\left\{ \begin{array}{cc} 1-\frac{a(i)}{b(i)},a(i)<b(i) \\ 0, \qquad a(i)=b(i) \\ \frac{a(i)}{b(i)}-1,a(i)>b(i) \end{array} \right. \]

• s(i)s(i)接近1，则说明样本ii聚类合理
• s(i)s(i)接近-1，则说明样本ii更应该分类到其他类
• s(i)s(i)接近0，则说明样本ii在两个类的边界上

聚类模型评价：Rand指数

Rand指数(Rand Index，RI)类似于分类模型中的准确度指标，其具体定义如下：

• 设数据集XX的一个聚类结构为

C ={C_1,C_2,\dots, C_m}C=C1,C2,…,C**m

• 数据集已知的划分为

P ={ P_1,P_2,\dots,P_s }P=P1,P2,…,P**s ,

• 可通过比较CC和PP的混淆矩阵来评价聚类的质量。

纯度(Purity)方法是极为简单的一种聚类评价方法，只需计算正确聚类的文档数占总文档数的比例

互信息(Mutual Information)是纯度的另一种表述，作用与纯度（Purity）一致。建立在熵的概念基础上，又称信息增益。

查看sklearn的帮助文档

• 我们可以通过help()函数来查看sklearn的帮助文档
  • 导入sklearn库：import sklearn
  • 查看sklearn帮助：help(sklearn)