python 常见的较为基础的算法题解析

1. 结尾0的个数

给你一个正整数列表 L, 输出L内所有数字的乘积末尾0的个数。(提示:不要直接相乘,数字很多,相乘得到的结果可能会很大)。

输入示例

输入：L=[2,8,3,50]

输出示例

输出：2

解析

所有元素相乘, 算最后是有几个0, 如果 [2, 5] 相乘后 是 10 , 0 个数位 1

本质上为了避免最后数字太大, 则每次乘算完了再除以 10 一次一次叠加即可

代码

import functools
import collections


def func(data):
    num = 1
    c_num = 0
    for i in data:
        num *= i
        while num % 10 == 0:
            num //= 10
            c_num += 1

    return c_num


def test(data):
    res = collections.Counter(str(functools.reduce(lambda x, y: x * y, data)))
    return res.get("0")


if __name__ == '__main__':
    data_1 = [2, 8, 3, 50]
    print(func(data_1))
    print(test(data_1))
    data_2 = [2, 8, 3, 50, 6]
    print(func(data_2))
    print(test(data_2))
    data_3 = [2, 8, 3, 50, 6, 5]
    print(func(data_3))
    print(test(data_3))

    """
    2
    2
    2
    2
    3
    3
    """

2. 结尾非零数的奇偶性

给你一个正整数列表 L, 判断列表内所有数字乘积的最后一个非零数字的奇偶性。如果为奇数输出1,偶数则输出0。

输入示例

输入：L=[2,8,3,50]

输出示例

输出：0

解析

在上题的基础上的改造题, 这里直接用另一种方式字符串来处理, 转换成字符串后剔除掉所有的0后的的部分能否整除2即可判断

代码

import functools


def func(data):
    a_num = 1
    for i in data:
        a_num *= i
        while str(a_num).endswith("0"):
            a_num = str(a_num)[:-1]
            a_num = int(a_num)
    return a_num % 2
    # 最后的数字不重要, 不用最后的算也是一样的
    # last_num = int(str(a_num)[-1])
    # print(last_num)
    # return last_num % 2


def test(data):
    return int(str(functools.reduce(lambda x, y: x * y, data)).split("0")[0]) % 2



if __name__ == '__main__':
    data_1 = [1, 7, 77, 77, 777]
    print(test(data_1))
    print(func(data_1))
    data_2 = [1, 2, 3, 4]
    print(test(data_2))
    print(func(data_2))
    
    """
    1
    1
    0
    0
    """

3. 光棍的悲伤

光棍们对1总是那么敏感，因此每年的11.11被戏称为光棍节。小Py光棍几十载，光棍自有光棍的快乐。

让我们勇敢地面对光棍的身份吧，现在就证明自己：给你一个整数a，数出a在二进制表示下1的个数，并输出。

输入示例

输入：a = 7

输出示例

输出：3

解析

7的二进制是111，所以输出答案是3。这道题考的是如何将十进制整数转化为二进制数，方法就是：除二取余，逆序读取

因为判断是1 的个数, 所以计算 1 既可以

代码

import collections


def func(num):
    c_num = 0
    while num:
        if num % 2:
            c_num += 1
        num //= 2
    return c_num


def test(num):
    print(bin(num))
    return collections.Counter(str(bin(num))).get("1")


if __name__ == '__main__':
    data_1 = 7
    print(test(data_1))
    print(func(data_1))
    data_2 = 10
    print(test(data_2))
    print(func(data_2))

    """
    0b111
    3
    3
    0b1010
    2
    2
    """

4. 判断三角形

给你三个整数a,b,c, 判断能否以它们为三个边长构成三角形。 若能，输出YES，否则输出NO

输入示例

输入：a = 5 b = 5 c = 5

输出示例

输出：YES

解析

三角形任意两边之和大于第三边，可以利用列表排序求出较小的两边，然后相加再和第三边比较，进行判断

代码

def func(a, b, c):
    m_num = max(max(a, b), c)
    s_num = a + b + c
    return m_num < s_num - m_num


if __name__ == '__main__':
    res = func(1, 2, 2)
    print(res)

5. 公约数的个数

给你两个正整数a,b, 输出它们公约数的个数。

输入示例

输入：a = 24 b = 36

输出示例

输出：6

解析

从1到两数较小的数，看看是否可以同时被两数整除，若可以则结果加一

基于此题可以继续延展, 

代码

def func(a, b):
    num = 0
    for i in range(1, min(a, b) + 1):
        if a % i == 0 and b % i == 0:
            num += 1
    return num


if __name__ == '__main__':
    res = func(24, 36)
    print(res)  // 6

6. 公约数的个数

我们经常遇到的问题是给你两个数，要你求最大公约数和最小公倍数。今天我们反其道而行之，给你两个数a和b，

计算出它们分别是哪两个数的积的最大公约数和最小公倍数。输出这两个数，小的在前，大的在后，以空格隔开。

若有多组解，输出它们之和最小的那组。

输入示例

输入：a=3, b = 60

输出示例

输出：12 15

解析

最大公约数与最小公倍数的乘积就是所求的两数之积

然后题目要求两数和最小，在两数积不变的情况下，二者越接近，和越小。

所以从积的平方根开始，求第一个能被积整除的数即可

代码

def func(a, b):
    j = a * b
    for i in range(1, j + 1):
        _ = j / i
        if j % i == 0 and i >= j / i:
            return [int(j / i), i]


if __name__ == '__main__':
    res = func(3, 60)
    print(res)  # [12, 15]

8. 回文子串

给你一个字符串a和一个正整数n,判断a中是否存在长度为n的回文子串。

如果存在，则输出YES，否则输出NO。

回文串的定义：记串str逆序之后的字符串是str1，若str=str1,则称str是回文串，如"abcba".

输入示例

输入：a = "abcba" n = 5

输出示例

输出：YES

解析

根据正整数n进行分割字符串，然后判断字符串是不是回文串。

由于python中字符串没有直接提供reverse函数（列表list有，但需要先将字符串转换为列表，较麻烦），

所以采用字符串切片。若一个字符串为s，其逆序为s[：：-1]，前两个空表示提取全部，-1表示逆序。

最常规的方法则是头尾指针前后移动, 然后这样可以从运算过程中就可以提前获得结果

代码

def func(s):
    pre = 0
    last = len(s) - 1
    flag = True
    while pre <= last:
        if s[pre] != s[last]:
            flag = False
            break
        pre += 1
        last -= 1

    return flag


def test_1(s):
    s_list = [i for i in s]
    s_list.reverse()
    rev_s = "".join(s_list)
    return rev_s == s


def test_2(s):
    return s[::-1] == s


if __name__ == '__main__':
    print(func("aabbcc"))
    print(test_1("aabbcc"))
    print(test_2("aabbcc"))
    print(func("abccba"))
    print(test_1("abccba"))
    print(test_2("abccba"))
    
    """
    False
    False
    False
    True
    True
    True
    """

9. 山峰的个数

十一假期,小P出去爬山,爬山的过程中每隔10米他都会记录当前点的海拔高度(以一个浮点数表示),

这些值序列保存在一个由浮点数组成的列表h中。

回到家中，小P想研究一下自己经过了几个山峰，请你帮他计算一下，

例如：h=[0.9,1.2,1.22,1.1,1.6,0.99], 将这些高度顺序连线，会发现有两个山峰，故输出一个2(序列两端不算山峰)

输入示例

输入：h = [0.9, 1.2, 1.22, 1.1, 1.6, 0.99]

输出示例

输出：2

解析

一次遍历即可，分别比较其与前一位和后一位的大小，注意列表不要越界

def func(s):
    if not s or len(s) < 3:
        return 0
    c_num = 0
    pre_i, cur_i, next_i = 0, 0, 1
    for i in s:
        if cur_i == 0 or cur_i == len(s) - 1:
            pre_i += 0
            cur_i += 1
            next_i += 1
            continue
        if i > s[pre_i] and i > s[next_i]:
            c_num += 1
        pre_i += 1
        cur_i += 1
        next_i += 1
    return c_num


if __name__ == '__main__':
    print(func([0.9, 1.2, 1.22, 1.1, 1.6, 0.99]))  # 2
    print(func([0.9, 1.2, 1.22, 1.1, 1.6, 0.99, 1.9, 1.3]))  # 3

10. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序

输入示例

输入： [0,1,0,3,12]

输出示例

输出： [1,3,12,0,0]

解析

双指针, 或者冒泡

冒泡: 　　    两次循环,  第一次循环是所有的元素, 第二次是未排序的元素

　　　　　  第一次循环的元素如果是 0 就跟所有未排序的元素进行互换, 将 0 换到最后面

　　　　　  然后继续下一个未排序的元素进行对比

x = [0, 8, 9, 0, 10, 0]

for i in range(len(x)):
    if x[i] == 0:
        for j in range(i, len(x)):
            if j + 1 < len(x) - i:
                x[j], x[j + 1] = x[j + 1], x[j]
print(x)

双指针: 　　设定一个指针 j 从 0 开始, 然后另一个指针遍历数组

　　　　　  将指针i,j先指向第一个元素，让i不断后移，如果i指向的是一个非零元素，

　　　　      那么将 i 指向元素的值直接填入 j 指向的位置，然后 j 指针后移；

    　　         如果 i 指向的是一个零元素，那么指针 i 就直接后移，而 j 不变。

　　　　      当 i 已经全部遍历完后，从 j 的位置开始，直接往后全部填入零。

x = [0, 8, 9, 0, 10, 0]

j = 0
for i, v in enumerate(x):
    if v != 0:
        x[i], x[j] = x[j], x[i]
        j += 1
print(x)  # [8, 9, 10, 0, 0, 0]

11. 有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

输入示例

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

输出示例

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

解析

如果是都是整数都是负数就过于简单了. 因此这题的本质是两个有序数组的组合后进行拆分并合并

方法比较多, 比如先找出最中心的数字后转换成两个数组进行归并运算, 但是双指针方法是最简单的

截止条件定在为正负分界线上, 一旦达到表示其中一个数字遍历完毕, 剩下的直接进行追加即可

x = [-7, -5, -3, -1, 2, 4, 8, 10]

res = []
i = 0
j = len(x) - 1

while x[i] < x[j]:
    if x[i] * x[i] > x[j] * x[j]:
        res.insert(0, x[i] * x[i])
        i += 1
    else:
        res.insert(0, x[j] * x[j])
        j -= 1

for each in x[i:j]:
    res.insert(0, each * each)

print(res)

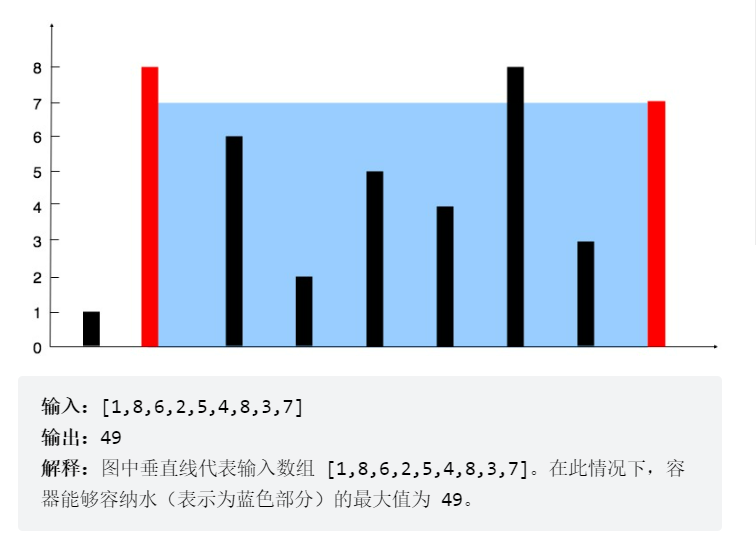
12. 盛最多水的容器

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。

在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

输入示例

输出示例

输入：height = [1,1]
输出：1

解析

运用双指针 + 贪心算法

前后各一个指针往中间移动,  贪心算法每次保留最大值

具体的移动逻辑: 对比前后指针的所在柱子的高度. 高度低的那个进行移动, 左指针往右移, 右指针往左移

x = [1, 8, 6, 2, 5, 4, 8, 3, 7]
# x = [1, 1]

res = []
i = 0
j = len(x) - 1
max_num = 0
while i < j:
    max_num = max(max_num, min(x[i], x[j]) * (j - i))
    if x[i] < x[j]:
        i += 1
    else:
        j -= 1

print(max_num)  # 49

13. 颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，

原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

输入示例

[2,0,2,1,1,0] 

输出示例

[0,0,1,1,2,2]

解析

 使用计数器计算出来 0, 1, 2 的数量之后对数组进行重构

但是此方法不算是特别合理, 没有做到原地排序

import collections

x = [2, 0, 2, 1, 1, 0]

c = collections.Counter(x)

res = []
for i in [0, 1, 2]:
    res.extend([i for each in range(c[i])])

print(res)  # [0, 0, 1, 1, 2, 2]

 

三指针操作, p0 设定为 0 的最后一个索引, p2 设定为 2 的最开始的索引. 

遇到 0 更新 p0 往后一位, 

x = [2, 0, 2, 1, 1, 0]

p_0_last = cur = 0
p_2_first = len(x) - 1

while cur < p_2_first:
    if x[cur] == 0:
        x[cur], x[p_0_last] = x[p_0_last], x[cur]
        cur += 1
        p_0_last += 1
    elif x[cur] == 2:
        x[cur], x[p_2_first] = x[p_2_first], x[cur]
        p_2_first -= 1
    else:
        cur += 1

print(x)

14. 递增的三元子序列

给定一个未排序的数组，判断这个数组中是否存在长度为 3 的递增子序列。

输入示例

输入: [1,2,3,4,5] 输出: true 示例 2: 输入: [5,4,3,2,1] 输出: false

输出示例

输入: [1,2,3,4,5] 输出: true 示例 2: 输入: [5,4,3,2,1] 输出: false

解析

 注意题意是可以不连续, 比如 [5, 3,6, 3, 2] 中的  [5, 3, 2] 即满足了要求可以作为递增的三序列

本题用到贪心算法

缓存下来前三序列的前两个数字, 最小值和中间值, 中间值默认给到正无穷, 最小值给到一个元素

然后不断更新最小的数字和中间数

每次对比, 如果当前的值比中间数大则表示找到了

若比中间值小但是比最小值大则更新 中间值

若比最小值还小. 则更新最小值, 但是注意此时最小值的数字的位置其实是比中间值的数字位置后面的

但是中间值前面还是存在一个数字比中间值小的(就是被替换掉的老的最小值, 替换掉了不代表就不存在了.)

比对依旧成立, 依次遍历到最后即可

class Solution:
    def increasingTriplet(self, nums) -> bool:
        n = len(nums)
        if n < 3:
            return False
        first, second = nums[0], float('inf')
        for i in range(1, n):
            num = nums[i]
            if num > second:
                return True
            if num > first:
                second = num
            else:
                first = num
        return False


if __name__ == '__main__':
    s = Solution()
    nums = [5, 1, 6]
    print(s.increasingTriplet(nums))

15. 和为s的连续正数序列

输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

输入示例

输入：target = 9
输出：[[2,3,4],[4,5]]

输出示例

输入：target = 15
输出：[[1,2,3,4,5],[4,5,6],[7,8]]

解析

 利用滑动窗口的原理, 记录当前窗口内的值的和

若和小于目标值. 右边界向右移动, 窗口扩大

若和大于目标值. 左边界向右移动, 窗口缩小, 抛弃之前的左边界的值, 此值做不到和为目标值

序列最少要求有两个数字, 至少两个数字相加才等于目标值, 且数字是递增. 则循环次数限制到 目标值的一半即可

def findContinuousSequence(target):
    i = 1  # 滑动窗口的左边界
    j = 1  # 滑动窗口的右边界
    sum = 0  # 滑动窗口中数字的和
    res = []

    while i <= target // 2:
        if sum < target:
            # 右边界向右移动
            sum += j
            j += 1
        elif sum > target:
            # 左边界向右移动
            sum -= i
            i += 1
        else:
            # 记录结果
            arr = list(range(i, j))
            res.append(arr)
            # 左边界向右移动
            sum -= i
            i += 1

    return res


if __name__ == '__main__':
    print(findContinuousSequence(9))

17. 除自身以外数组的乘积

给定长度为 n 的整数数组 nums，其中 n > 1，返回输出数组 output ，

其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积

输入示例

[1,2,3,4]

输出示例

[24,12,8,6]

解析

 不允许使用除法

 乘积 = 当前数左边的乘积 * 当前数右边的乘积

import functools


class Solution:
    def multiply(self, nums):
        res = []
        for i, v in enumerate(nums):
            left = 1 if i == 0 else functools.reduce(lambda x, y: x * y, nums[:i])
            right = 1 if i == len(nums) - 1 else functools.reduce(lambda x, y: x * y, nums[i + 1:])
            res.append(left * right)
        return res


if __name__ == '__main__':
    Solution().multiply([1, 2, 3, 4])

 

18. 杨辉三角

 

实现第n行是啥

输入示例

7

输出示例

[1, 6, 15, 20, 15, 6, 1]

解析

递归处理较为简单, 每层都是上层数据的叠加, 最顶层的 1和第二层的 1 1是确定的, 作为截止条件

tmp_dict = {}


def make_list(n):
    if tmp_dict.get(n):
        return tmp_dict[n]

    res = []
    if n == 1:
        return [1]
    if n == 2:
        return [1, 1]
    for i in range(n):
        if i == 0:
            res.append(1)
        elif i == n - 1:
            res.append(1)
            return res
        else:
            f_list = make_list(n - 1)
            res.append(f_list[i] + f_list[i - 1])
    tmp_dict[n] = res
    return res


print(make_list(7))  # [1, 6, 15, 20, 15, 6, 1]

 

19. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。 

输入示例

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

输出示例

输入：nums = [5,4,-1,7,8]
输出：23

解析

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

利用动态规划的思想, 找出具备一个子序列, 子序列的结尾的可能性是根据数组的每个元素来的

以 [5,4,-1,7,8] 为例,  找到最大值的子序列的全部的情况为

结尾为 5 的所有序列 + 结尾为 4 的所有序列 + ..... + 结尾为 8 的所有序列

然后问题在分化针对 每个元素的可能性进行先一轮的判断

结尾为 5 的所有序列中最大的一个序列  or 结尾为 4 的所有序列中最大的一个序列 or .....结尾为 8 的所有序列中最大的一个序列

这样核心的问题被分解成了两级的子问题来处理