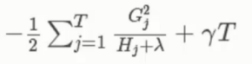机器学习 - 算法 - Xgboost 数学原理推导

工作原理

基于集成算法的多个树累加, 可以理解为是弱分类器的提升模型

公式表达

基本公式

目标函数

目标函数这里加入了损失函数计算

这里的公式是用的均方误差方式来计算

最优函数解

要对所有的样本的损失值的期望, 求解最小的程度作为最优解

集成算法表示

 集成算法中对所有的树进行累加处理

公式流程分解

每加一棵树都应该在之前基础上有一个提升

损失函数

叶子节点惩罚项

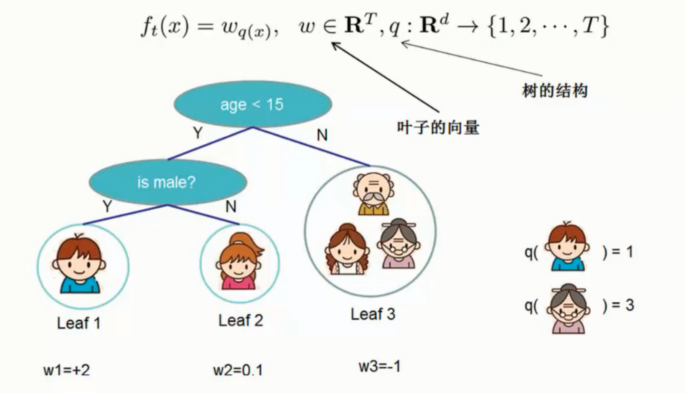
损失函数加入到基本公式目标函数中

多余出来的常数项就用 c 表示即可

目标函数推导

如上图. 三个树, 真实值 1000 , 第一棵树预测950, 残差 50 

第二颗就预测 30, 残差 20 , 一次类推最终结果预测 995 

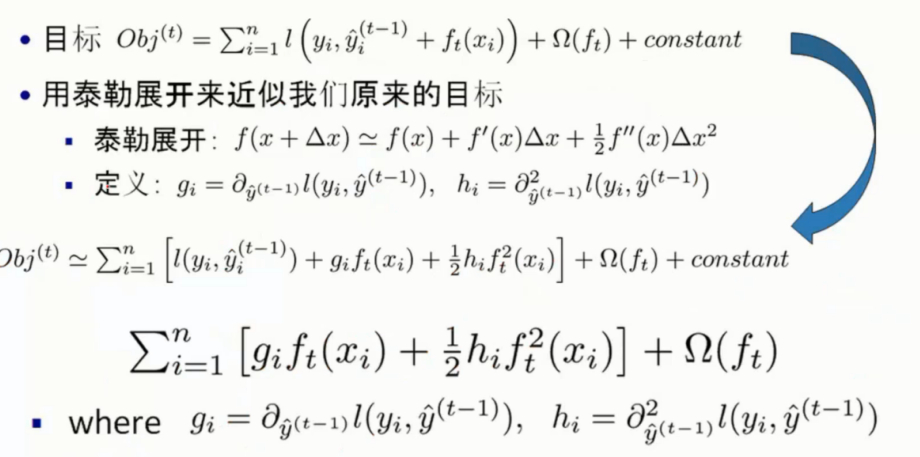
这里拟定近似成为了泰勒展开的形式

然后优化的时候, 对于  是对上一颗树的结果, 这个值对于下面是不会变动的

因此可以视为常数, 和最后面的常数项合并省略掉了

然后 gi 表示一阶导, hi 表示二阶导

去除掉常数项对极值不会有影响后

就剩下了 

 继续化简,   带入

  是对样本的遍历, 这样的话感觉和后面的 T 关系不大

在物理意义上所有的样本点都是会落到叶子节点上的

因此遍历样本和遍历叶子节点都是全部遍历到的

于是这里转换成对叶子节点的遍历 

对于每一个叶子节点则需要再遍历一次这个叶子节点上的所有样本  

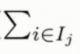
而包含有 w²_j   的两项可以进行合并从而得到了

 

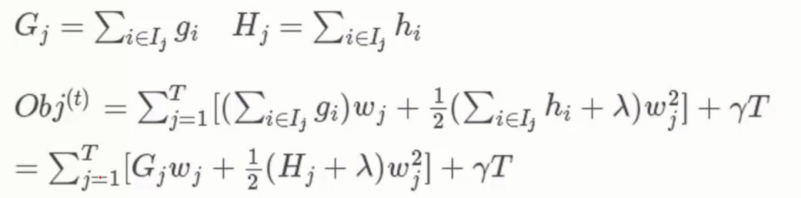
里面每个叶子节点的导数求和分别用 Gj 和 Hj 来表示一阶和二阶

从而进一步的化简得到最终的 目标函数

 目标函数求解

怎么样的 wj 可以让目标函数最小? 依旧是对 wj 偏导

然后求导等于0获得 wj 的表达式带入原函数

得最终解

其中对每一个Hj 和 Gj 都是可以得出的

以及 T 叶子节点数和 λ 都是已知的

目标函数使用实例

实际的操作中即可计算出每个叶子节点的一阶导二阶导

如果叶子中只有一个样本就按唯一的来算

多个就累加处理即可

而目标函数的的值越小则表示树结构越优

相比较之前的用熵值进行计算, 这里可以直接使用我们的目标函数的解来衡量判断模型

根据我们根据现有模型的值减去随机分割的左子树的值和右子树的值

然后这个值越大表示这时候的增益是最大的, 因此可以判断在哪里切是最优的