TOP

Python - 二叉树, 堆, headq 模块

二叉树

概念

二叉树是n(n>=0)个结点的有限集合，该集合或者为空集（称为空二叉树），

或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。

 

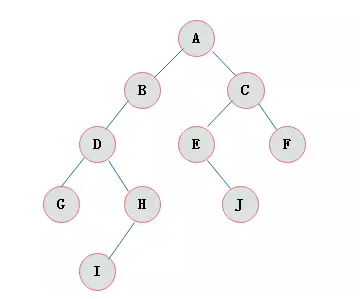
特点

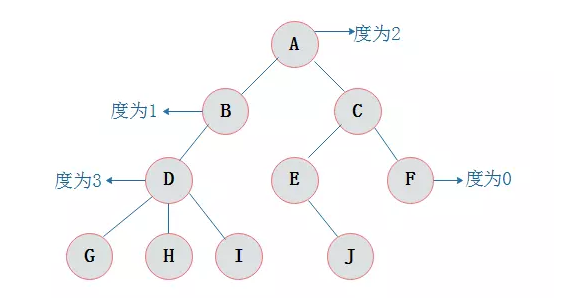
每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点

左子树和右子树是有顺序的，次序不能任意颠倒

即使树中某结点只有一棵子树，也要区分它是左子树还是右子树

性质

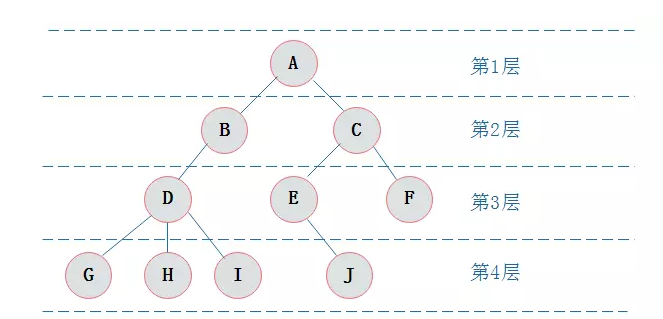
1）在二叉树的第 i 层上最多有 2i-1 个节点 。（i>=1）
2）二叉树中如果深度为k,那么最多有 2k-1 个节点。 (k>=1）
3）n0=n2+1 n0表示度数为0的节点数，n2表示度数为2的节点数。
4）在完全二叉树中，具有n个节点的完全二叉树的深度为[log2n]+1，其中[log2n]是向下取整。
5）若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号，则对完全二叉树中任意一个编号为 i 的结点有如下特性：
(1) 若 i=1，则该结点是二叉树的根，无双亲, 否则，编号为 [i/2] 的结点为其双亲结点;
(2) 若 2i>n，则该结点无左孩子，  否则，编号为 2i 的结点为其左孩子结点；
(3) 若 2i+1>n，则该结点无右孩子结点，  否则，编号为2i+1 的结点为其右孩子结点。

层

 

度

 

类型 

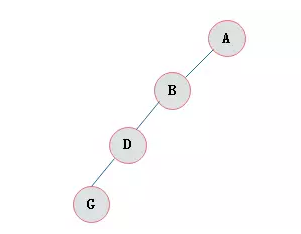
斜树

所有的结点都只有左子树的二叉树叫左斜树。

所有结点都是只有右子树的二叉树叫右斜树。

这两者统称为斜树。

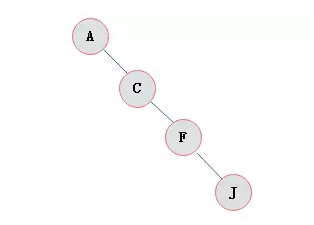
满二叉树

在一棵二叉树中。

如果所有分支结点都存在左子树和右子树，

并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点有：

　　1）叶子只能出现在最下一层。出现在其它层就不可能达成平衡。

　　2）非叶子结点的度一定是2。

　　3）在同样深度的二叉树中，满二叉树的结点个数最多，叶子数最多。

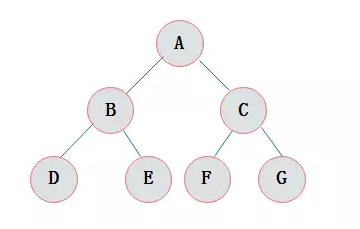
完全二叉树

对一颗具有n个结点的二叉树按层编号

如果编号为 i(1<=i<=n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同

则这棵二叉树称为完全二叉树。

特点

1）叶子结点只能出现在最下层和次下层。
2）最下层的叶子结点集中在树的左部。
3）倒数第二层若存在叶子结点，一定在右部连续位置。
4）如果结点度为1，则该结点只有左孩子，即没有右子树。
5）同样结点数目的二叉树，完全二叉树深度最小。
注：满二叉树一定是完全二叉树，但反过来不一定成立。

 


存储结构

顺序存储

二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，

并且结点的存储位置，就是数组的下标索引。

 

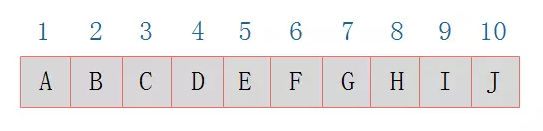
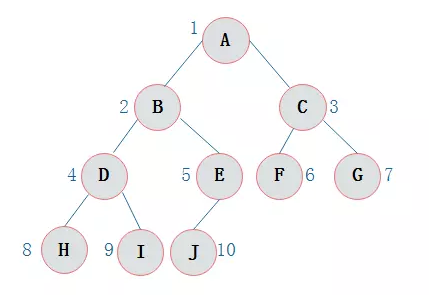
二叉链表

既然顺序存储不能满足二叉树的存储需求，那么考虑采用链式存储。

由二叉树定义可知，二叉树的每个结点最多有两个孩子。

因此，可以将结点数据结构定义为一个数据和两个指针域。

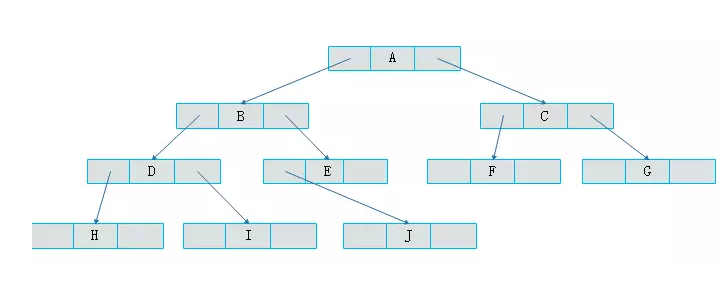
二叉树实现

定义一个左子树, 定义一个柚子树, 以及值

 class BinTree:  
     def __init__(self,value=None,left=None,right=None):  
         self.value=value  
         self.left=left    #左子树
         self.right=right  #右子树

二叉树遍历

先序遍历

先处理根, 之后是左子树, 然后是右子树

中序遍历

先处理左子树, 之后是根, 然后是右子树

后序遍历

先处理左子树, 之后是右子树, 最后是根

代码示例

def preTraverse(root):
    '''
    先序遍历
    '''
    if root is not None:
        print(root.value)
        preTraverse(root.left)
        preTraverse(root.right)


def midTraverse(root):
    '''
    中序遍历
    '''
    if root is not None:
        midTraverse(root.left)
        print(root.value)
        midTraverse(root.right)


def afterTraverse(root):
    '''
    后序遍历
    '''
    if root is not None:
        afterTraverse(root.left)
        afterTraverse(root.right)
        print(root.value)

堆

最大堆 / 最小堆

 

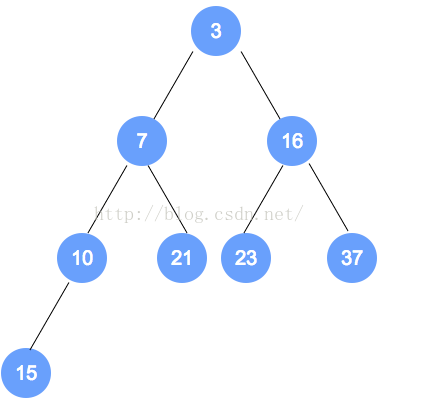
 最大 / 小堆是一棵完全二叉树，非叶子结点的值不大 / 小于左孩子和右孩子的值

构建原理

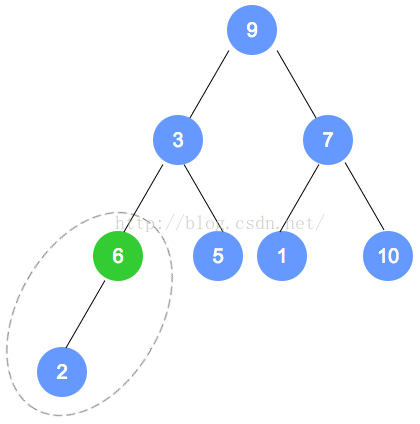
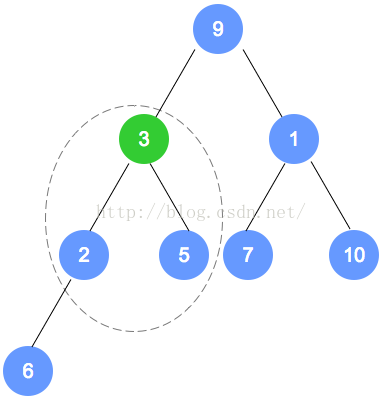
初始数组为：9,3,7,6,5,1,10,2

按照完全二叉树，将数字依次填入。

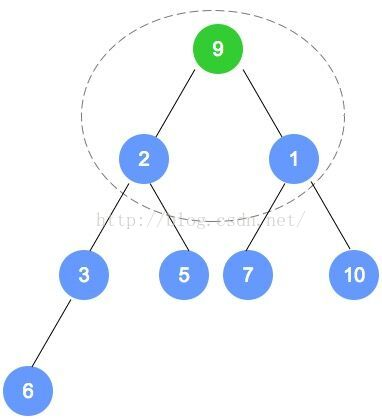
填入后，找到最后一个结点（本示例为数字2的节点），从它的父节点（本示例为数字6的节点）

开始调整。根据性质，小的数字往上移动；至此，第1次调整完成。

注意，被调整的节点，还有子节点的情况，需要递归进行调整。

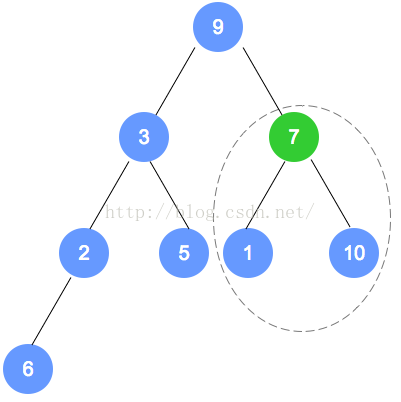
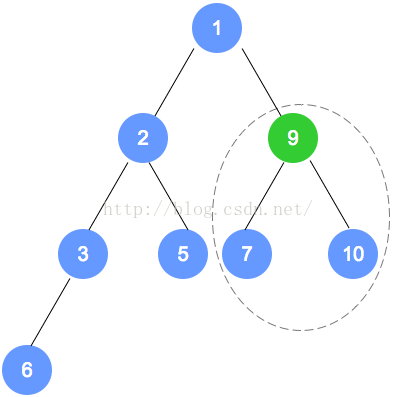
第二次调整，是数字6的节点数组下标小1的节点（比数字6的下标小1的节点是数字7的节点），

用刚才的规则进行调整。以此类推，直到调整到根节点。

 

 

 

 

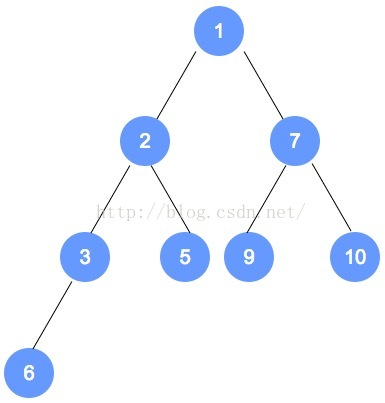
元素插入

以上个最小堆为例，插入数字0。

数字0的节点首先加入到该二叉树最后的一个节点，依据最小堆的定义，自底向上，递归调整。

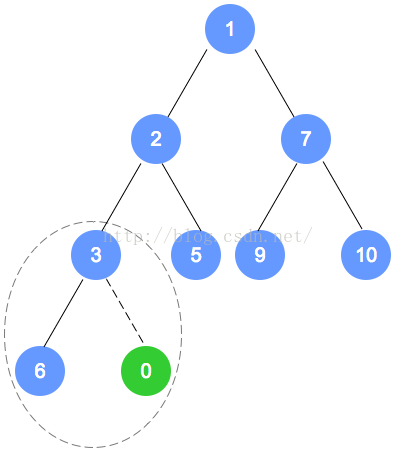
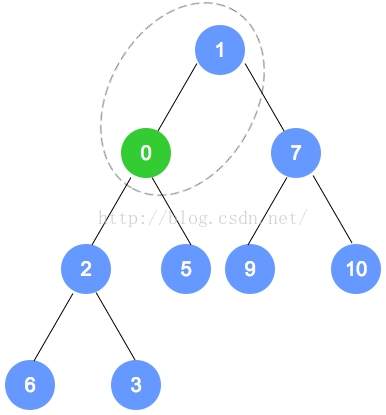
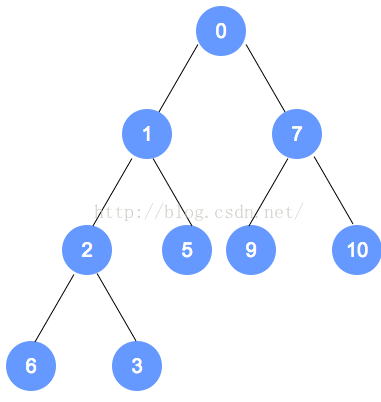
元素删除

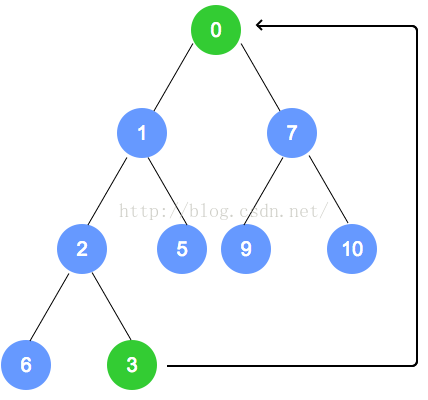
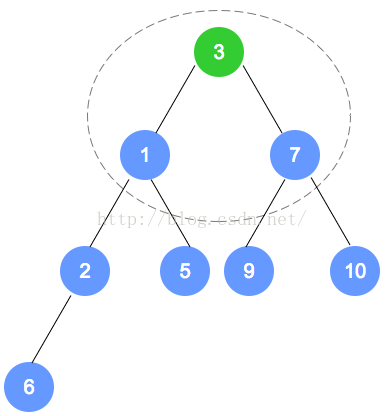
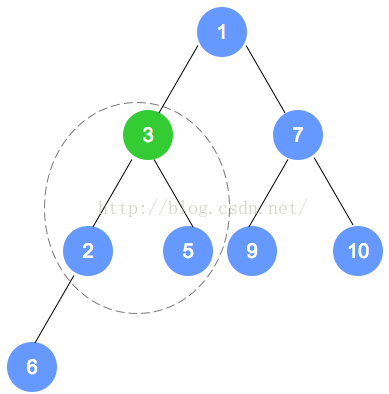
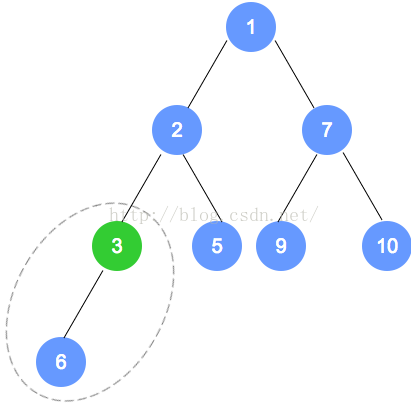
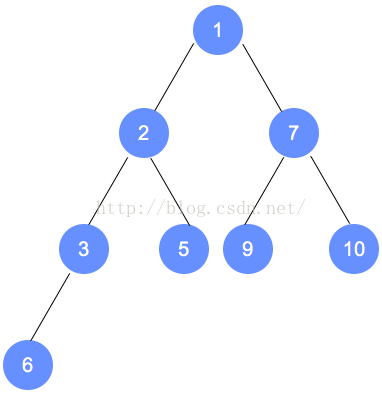
代码实现

最小堆

class MinHeap(object):
    """最小堆"""

    def __init__(self):
        self.data = []  # 创建堆
        self.count = len(self.data)  # 元素数量

    # def __init__(self, arr):
    #   self.data = copy.copy(arr)
    #   self.count = len(self.data)
    #   i = self.count / 2
    #   while i >= 1:
    #       self.shiftDown(i)
    #       i -= 1

    def size(self):
        return self.count

    def isEmpty(self):
        return self.count == 0

    def insert(self, item):
        # 插入元素入堆
        self.data.append(item)
        self.count += 1
        self.shiftup(self.count)

    def shiftup(self, count):
        # 将插入的元素放到合适位置，保持最小堆
        while count > 1 and self.data[(count / 2) - 1] > self.data[count - 1]:
            self.data[(count / 2) - 1], self.data[count - 1] = self.data[count - 1], self.data[(count / 2) - 1]
            count /= 2

    def extractMin(self):
        # 出堆
        if self.count > 0:
            ret = self.data[0]
            self.data[0], self.data[self.count - 1] = self.data[self.count - 1], self.data[0]
            self.data.pop()
            self.count -= 1
            self.shiftDown(1)
            return ret

    def shiftDown(self, count):
        # 将堆的索引位置元素向下移动到合适位置，保持最小堆
        while 2 * count <= self.count:
            # 证明有孩子
            j = 2 * count
            if j + 1 <= self.count:
                # 证明有右孩子
                if self.data[j] < self.data[j - 1]:
                    j += 1
            if self.data[count - 1] <= self.data[j - 1]:
                # 堆的索引位置已经小于两个孩子节点，不需要交换了
                break
            self.data[count - 1], self.data[j - 1] = self.data[j - 1], self.data[count - 1]
            count = j

最大堆

"""
最大堆
"""


class MaxHeap(object):
    # def __init__(self):
    #   self.data = []  # 创建堆
    #   self.count = len(self.data)  # 元素数量

    def __init__(self, arr):
        self.data = copy.copy(arr)
        self.count = len(self.data)
        i = self.count / 2
        while i >= 1:
            self.shiftDown(i)
            i -= 1

    def size(self):
        return self.count

    def isEmpty(self):
        return self.count == 0

    def insert(self, item):
        # 插入元素入堆
        self.data.append(item)
        self.count += 1
        self.shiftup(self.count)

    def shiftup(self, count):
        # 将插入的元素放到合适位置，保持最大堆
        while count > 1 and self.data[(count / 2) - 1] < self.data[count - 1]:
            self.data[(count / 2) - 1], self.data[count - 1] = self.data[count - 1], self.data[(count / 2) - 1]
            count /= 2

    def extractMax(self):
        # 出堆
        if self.count > 0:
            ret = self.data[0]
            self.data[0], self.data[self.count - 1] = self.data[self.count - 1], self.data[0]
            self.data.pop()
            self.count -= 1
            self.shiftDown(1)
            return ret

    def shiftDown(self, count):
        # 将堆的索引位置元素向下移动到合适位置，保持最大堆
        while 2 * count <= self.count:
            # 证明有孩子
            j = 2 * count
            if j + 1 <= self.count:
                # 证明有右孩子
                if self.data[j] > self.data[j - 1]:
                    j += 1
            if self.data[count - 1] >= self.data[j - 1]:
                # 堆的索引位置已经大于两个孩子节点，不需要交换了
                break
            self.data[count - 1], self.data[j - 1] = self.data[j - 1], self.data[count - 1]
            count = j

heapq 模块

官方文档    这里

Python 自带的用于堆结构方便的模块

创建堆 - 最小堆

单个添加创建堆 - heappush

import heapq

data = [1,5,3,2,8,5]
heap = []

for n in data:
    heapq.heappush(heap, n)

对已存在的序列转化为堆 - heapify

import heapq

data = [1,5,3,2,8,5]
heapq.heapify(data)

对多个序列转化为堆 - merge

import heapq

num1 = [32, 3, 5, 34, 54, 23, 132]
num2 = [23, 2, 12, 656, 324, 23, 54]
num1 = sorted(num1)
num2 = sorted(num2)

res = heapq.merge(num1, num2)
print(list(res))  # [2, 3, 5, 12, 23, 23, 23, 32, 34, 54, 54, 132, 324, 656]

创建堆 - 最大堆

用法同最小堆, 创建的时候将所有的值取相反数

然后在取出堆顶, 在进行取反, 即可获得原值

import heapq

data = [1, 5, 3, 2, 8, 5]
li = []
for i in data:
    heapq.heappush(li, -i)

print(li)  # [-8, -5, -5, -1, -2, -3]
print(-li[0])  # 8

访问堆内容

查看最小值 - [0]

import heapq

data = [1, 5, 3, 2, 8, 5]
heapq.heapify(data)

print(data[0]) # 1

弹出最小值 - heappop

会改变原数据, 类似于列表的 pop

import heapq

data = [1, 5, 3, 2, 8, 5]
heapq.heapify(data)

print(heapq.heappop(data))  # 1
print(data)  # [2, 5, 3, 5, 8]

向堆内推送值 - heappush

import heapq

data = [1, 5, 3, 2, 8, 5]
heapq.heapify(data)

heapq.heappush(data, 10)
print(data)  # [1, 2, 3, 5, 8, 5, 10]

弹出最小值并加入一个值 - heappushpop

 弹出最小值, 添加新值, 且自动排序保持是最小堆

import heapq

data = [1, 5, 3, 2, 8, 5]
heapq.heapify(data)

print(heapq.heappushpop(data, 1))  # 1
print(data)  # [1, 2, 3, 5, 8, 5]

弹出最小值并加入一个值 - heapreplace

弹出最小值, 添加新值, 且自动排序保持是最小堆

是 heappushpop 的高效版本, 在py3 中适用

import heapq

data = [1, 5, 3, 2, 8, 5]
heapq.heapify(data)

print(heapq.heapreplace(data, 10))  # 1
print(data)  # [2, 5, 3, 10, 8, 5]

k 值问题 - nlargest / nsmallest 

找出堆中最小 / 大的 k 个值

import heapq

data = [1, 5, 3, 2, 8, 5]

heapq.heapify(data)
print(data)  # [1, 2, 3, 5, 8, 5]
print(heapq.nlargest(2, data))  # [8, 5]
print(heapq.nsmallest(2, data))  # [1, 2]

 可以接收一个参数 key , 用于指定选项进行选取

用法类似于 sorted 的 key

import heapq
from pprint import pprint
portfolio = [
    {'name': 'IBM', 'shares': 100, 'price': 91.1},
    {'name': 'AAPL', 'shares': 50, 'price': 543.22},
    {'name': 'FB', 'shares': 200, 'price': 21.09},
    {'name': 'HPQ', 'shares': 35, 'price': 31.75},
    {'name': 'YHOO', 'shares': 45, 'price': 16.35},
    {'name': 'ACME', 'shares': 75, 'price': 115.65}
]
cheap = heapq.nsmallest(3, portfolio, key=lambda s: s['price'])
expensive = heapq.nlargest(3, portfolio, key=lambda s: s['price'])
pprint(cheap)
pprint(expensive)

"""
输出：
[{'name': 'YHOO', 'price': 16.35, 'shares': 45},
 {'name': 'FB', 'price': 21.09, 'shares': 200},
 {'name': 'HPQ', 'price': 31.75, 'shares': 35}]
[{'name': 'AAPL', 'price': 543.22, 'shares': 50},
 {'name': 'ACME', 'price': 115.65, 'shares': 75},
 {'name': 'IBM', 'price': 91.1, 'shares': 100}]
"""

 

posted @ 2019-05-15 17:12  羊驼之歌  阅读(1435)  评论(0)  编辑  收藏  举报