/*
求解单源最短路问题：Bellman-Ford算法（可判负权回路）
注：
负权回路： 如果存在一个回路（首尾相同的路径），而且这个回路上所有权值之和是负数，那这就是一个负权回路。
f[i] := 从起点s出发到节点i的最短距离
故：
f[i] = min(f[j] + dis[i][j])
初始值：
f[] = INF
f[s] = 0;
自己当时遇到的疑惑，以及参考了相关资料获得的解答：
（1）在实现时，最外侧循环的迭代次数为什么最大是|V|-1次？（|V|节点的个数）
答： 前提：在图中不存在负权回路
一共有n个节点，求1->n的最短距离，我们知道1->n的最短路径，最多有(n-1)条边。
（如果大于(n-1)，说明有一个节点在最短路径上走了两次，即走了一个圈，
若圈的权为正：显然包含整个圈的路径必定不是最短路径；
若圈的权为负：最短路径不存在，因为到达节点的路径距离可以无限变小；
若圈的权为0： 去掉之后不影响最优解。
）
在每次循环中，我们利用f[i] = min(f[j] + dis[i][j])来更新(s->i)的边，每
次循环必定会更新成功一条边（更新成功指的是：这条边的权值也是最终最短路径的权值），
那么需要(n-1)次循环才可以更新掉所有的边。
在《数据结构与编程实验--大学生程序设计课程与竞赛训练教材》（http://book.douban.com/subject/10537877/）上，
有说到：
很多时候，需要的迭代次数远小于|V|-1，所以可以考虑在每次循环中设置的update的标记，
如果没有update，则说明已获得最优解，跳出循环即可。
时间复杂度：O(V*E)
（2）为什么如果f[i]>f[j]+dis[j][i]，可以判定有负权回路？
答： 根本原因：求解最短路时 f[i] = min(f[j] + dis[i][j])
在|V|-1此循环结束，即已获得最优解，如果在图中不存在负权回路，那么必然是f[i]<=f[j]+dis[j][i]，
否则必然存在s->i的路径距离比f[i]更短，与已获得最优解矛盾。
代码：
for (int i = 0; i < eg.size(); ++i)
{
if (f[eg[i].egto] > f[eg[i].egfrom] + eg[i].egfrom)
{
return false; // 出现负权回路
}
return true; // 没有出现负权回路
}
eg:
初始：
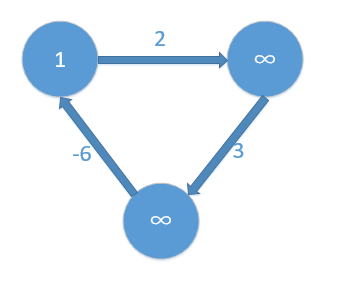
边更新后：
3 > 0 + 2 => 出现负权回路
-------------------------------------------------------
poj 3268 Silver Cow Party
what is the longest amount of time a cow must spend walking to the party and back？
故此题需要解决两个问题：
（1）所有节点到达节点X的最短距离；
对于此问题，可以反过来想：从X节点到达所有节点的最短距离，答案不变。
但是此时初始存储的有向边的方向需要调换
（原因：路是单向的，a->b反过来想a<-b，边的方向发生了改变，
边的权值不变，求解a->b的最短路也就是求a<-b的最短路
）
（2）节点X到达所有节点的最短距离。
按初始存储的有向边进行计算
答案：
max{ walkTo[i]+returnTo[i] }
*/
1 #include <iostream>
2 #include <cstdlib>
3 #include <cstdio>
4 #include <cstddef>
5 #include <iterator>
6 #include <algorithm>
7 #include <string>
8 #include <locale>
9 #include <cmath>
10 #include <vector>
11 #include <cstring>
12 #include <map>
13 #include <utility>
14 #include <queue>
15 #include <stack>
16 #include <set>
17 using namespace std;
18 const int INF = 0x3f3f3f3f;
19 const int MaxN = 205;
20 const int modPrime = 3046721;
21
22 struct Edge
23 {
24 int egfrom, egto, egcost;
25 };
26
27 int N, M, X;
28 Edge eg[100010];
29 int walkTo[1010]; // cow walk to the party
30 int returnTo[1010]; // cow return to her farm
31
32 void Solve()
33 {
34 bool update = true;
35 fill(walkTo, walkTo + 1010, INF);
36 walkTo[X] = 0;
37 for (int i = 0; i < N && update; ++i)
38 {
39 update = false;
40 for (int j = 0; j < M; ++j)
41 {
42 if ((walkTo[eg[j].egto] != INF) && (walkTo[eg[j].egfrom] > walkTo[eg[j].egto] + eg[j].egcost))
43 {
44 walkTo[eg[j].egfrom] = walkTo[eg[j].egto] + eg[j].egcost;
45 update = true;
46 }
47 }
48 }
49
50 fill(returnTo, returnTo + 1010, INF);
51 returnTo[X] = 0;
52 update = true;
53 for (int i = 0; i < N && update; ++i)
54 {
55 update = false;
56 for (int j = 0; j < M; ++j)
57 {
58 if ((returnTo[eg[j].egfrom] != INF) && (returnTo[eg[j].egto] > returnTo[eg[j].egfrom] + eg[j].egcost))
59 {
60 returnTo[eg[j].egto] = returnTo[eg[j].egfrom] + eg[j].egcost;
61 update = true;
62 }
63 }
64 }
65
66 int ans = 0;
67 for (int i = 1; i <= N; ++i)
68 {
69 ans = max(ans, walkTo[i] + returnTo[i]);
70 }
71 cout << ans << endl;
72 }
73
74 int main()
75 {
76 #ifdef HOME
77 freopen("in", "r", stdin);
78 //freopen("out", "w", stdout);
79 #endif
80
81 cin >> N >> M >> X;
82 for (int i = 0; i < M; ++i)
83 {
84 cin >> eg[i].egfrom >> eg[i].egto >> eg[i].egcost;
85 }
86 Solve();
87
88
89 #ifdef HOME
90 cerr << "Time elapsed: " << clock() / CLOCKS_PER_SEC << " ms" << endl;
91 _CrtDumpMemoryLeaks();
92 #endif
93 return 0;
94 }
