最大子序和(动态规划)

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。（只求最大子序和，不是最大子序区间）

思路

假设 nums 数组的长度是 n，下标从 0 到 n - 1。

我们用 ai 代表 nums[i]，用 f(i)代表以第 i个数结尾的「连续子数组的最大和」，那么很显然我们要求的答案就是：

 

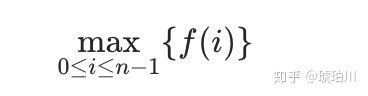
 因此我们只需要求出每个位置的 f(i)，然后返回 f 数组中的最大值即可。那么我们如何求 f(i)呢？我们可以考虑 ai​ 单独成为一段还是加入 f(i - 1) 对应的那一段，这取决于 ai和 f(i - 1) + ai的大小，我们希望获得一个比较大的，于是可以写出这样的动态规划转移方程：

 

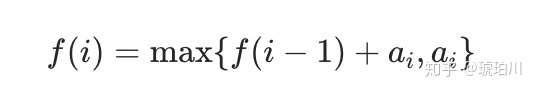
    public int maxSubArray(int[] nums) {
        int[] f = new int[nums.length];
        f[0] = nums[0];
        int max = f[0];
        for(int i = 1;i<nums.length;i++) {
            f[i] = Math.max(f[i-1]+nums[i],nums[i]);
            max = Math.max(f[i],max);
        }
        return max;
    }