常见树的概念

以左为尊，根据根结点的所在顺序，将二叉树的遍历分为三种：
先序遍历：根左右，根在先。
中序遍历：左根右，根在中。
后序遍历：左右根，根在后。

        
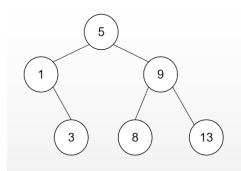
一.《二叉查找树》又叫二叉搜索树或二叉排序树。它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉树。 中序遍历可以得到顺序的结点值。

 

 

二.《平衡二叉树》又称AVL树，指的是左子树上的所有节点的值都比根节点的值小，而右子树上的所有节点的值都比根节点的值大，且左子树与右子树的高度差最大为1。因此，平衡二叉树满足所有二叉排序（搜索）树的性质。至于AVL，则是取自两个发明平衡二叉树的科学家的名字：G. M. Adelson-Velsky和E. M. Landis。

 

 

《三》红黑树 (Red-Black Tree )

 二叉平衡树的严格平衡策略以牺牲建立查找结构(插入，删除操作)的代价，换来了稳定的O(logN) 的查找时间复杂度。但是这样做是否值得呢？ 能不能找一种折中策略，即不牺牲太大的建立查找结构的代价，也能保证稳定高效的查找效率呢？ 答案就是：红黑树。
RBT 的操作代价分析：
(1) 查找代价： 由于红黑树的性质(最长路径长度不超过最短路径长度的2倍)，可以说明红黑树虽然不像AVL一样是严格平衡的，但平衡性能还是要比BST要好。其查找代价基本维持在O(logN)左右，但在最差情况下(最长路径是最短路径的2倍少1)，比AVL要略逊色一点。
(2) 插入代价： RBT插入结点时，需要旋转操作和变色操作。但由于只需要保证RBT基本平衡就可以了。因此插入结点最多只需要2次旋转，这一点和AVL的插入操作一样。虽然变色操作需要O(logN)，但是变色操作十分简单，代价很小。
(3) 删除代价： RBT的删除操作代价要比AVL要好的多，删除一个结点最多只需要3次旋转操作。 RBT 效率总结 : 查找 效率最好情况下时间复杂度为O(logN)，但在最坏情况下比AVL要差一些，但也远远好于BST。 插入和删除操作改变树的平衡性的概率要远远小于AVL（RBT不是高度平衡的）。因此需要的旋转操作的可能性要小，而且一旦需要旋转，插入一个结点最多只需要旋转2次，删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN)，但是实际上，这种操作由于简单所需要的代价很小。

红黑树为什么不适合做索引？

在大规模数据存储的时候，红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁，进而导致效率低下的情况。
   
三.《B树》多路平衡搜索树，所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

如下图所示为一个3阶的B-Tree：

 

 

 

模拟查找关键字29的过程：

1.根据根节点找到磁盘块1，读入内存。【磁盘I/O操作第1次】（实际中根结点常驻内存，不需要I/O）
比较关键字29在区间（17,35），找到磁盘块1的指针P2。
2.根据P2指针找到磁盘块3，读入内存。【磁盘I/O操作第2次】
比较关键字29在区间（26,30），找到磁盘块3的指针P2。
3.根据P2指针找到磁盘块8，读入内存。【磁盘I/O操作第3次】
在磁盘块8中的关键字列表中找到关键字29。
分析上面过程，发现需要3次磁盘I/O操作，和3次内存查找操作。由于内存中的关键字是一个有序表结构，可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数，使每次磁盘I/O取到内存的数据都发挥了作用，从而提高了查询效率。

 

 

      
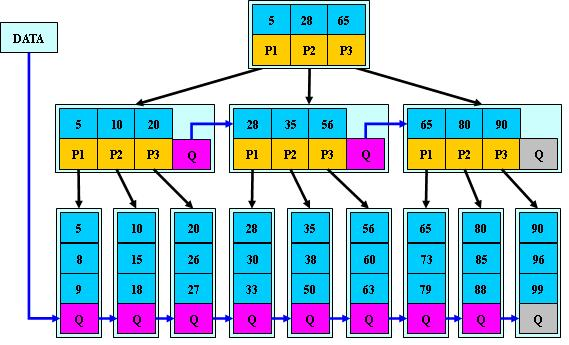
四《B+树》

B树有许多变种，其中最常见的是B+Tree，例如MySQL就普遍使用B+Tree实现其索引结构。
与B树相比，B+Tree有以下不同点：
1. 非叶子结点不存储data，只存储key和指针。
2.所有非叶子结点的key（主键）在叶子结点中都存在，非叶子结点作为叶子结点的索引，B+树总是到叶子结点才命中
3.带有顺序访问指针的B+Tree
在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能。
例如图中如果要查询key为从15到60的所有数据记录，当找到15后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点，极大提到了区间查询效率。

 

 

 

 

 

      
B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；