二分查找算法的应用

二分查找算法

 

 1.旋转数组中的最小数字:(3,4,5,1,2 为 1,2,3,4,5 的一个旋转)

 

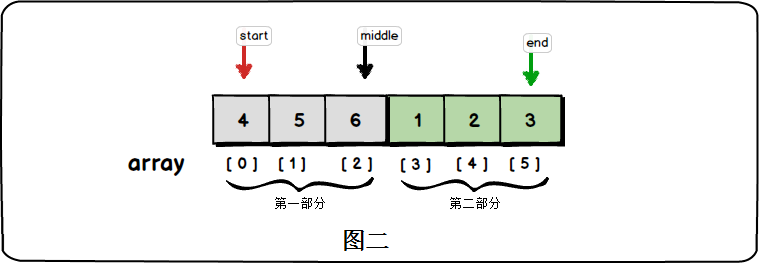
正如上图所示:我们计算中间的位置 middle 如果说 arr[middle] >= arr[start] 说明 middle 落在了前面的递增区间上,middle = start 缩小查找范围.

同理,如果arr[middle] <= arr[end] 则将 end = middle

这里呢有一个问题:

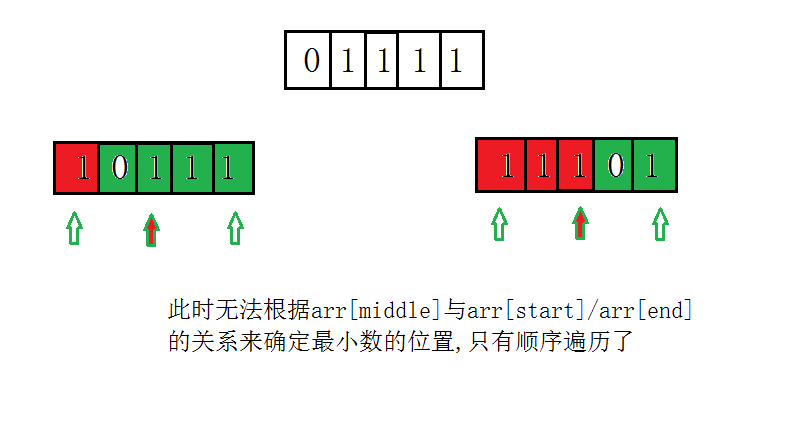
int MinInorder(int* arr, int start, int end)
{
    int result = arr[start];
    bool check = false;
    while (start <= end)
    {
        ++start;
        if (arr[start] < result)
            return arr[start];
    }
    return result;
}

int Min(int* arr, int lenth)
{
    if (arr == NULL || lenth <= 0)
    {
        cout << "Error:Invalid Parameters" << endl;
        return 0;
    }
    int start = 0, middle, end = lenth - 1;
    while (start < end)
    {
        middle = (end - start) / 2 + start;
        if (end - start == 1)
            return arr[end];
        if (arr[middle] == arr[start] && arr[middle] == arr[end])
            return MinInorder(arr + start, start, end);
        if (arr[middle] >= arr[start])  //非特例情况下
            start = middle;
        else
            end = middle;
    }
}

 

 

2.旋转数组中查找某一个数:（7，8，9，1，2，3，4，5，6 中找 1 返回 3）

 

 

int Inorder(int* arr, int left, int right,int key)
{
    for (int i = left; i <= right; ++i)
    {
        if (arr[i] == key)
            return i;
    }
    return -1;
}

int BinarySearch(int* arr, int left, int right, int key)
{
    if (left <= right)
    {
        int middle = (right - left) / 2 + left;
        if (arr[middle] > key)
        {
            right = middle - 1;
            return BinarySearch(arr, left, right, key);
        }
        else if (arr[middle] < key)
        {
            left = middle + 1;
            return BinarySearch(arr, left, right, key);
        }
        else
            return middle;
    }
    return -1;
}

int RotateArray(int* arr, int _left,int _right, int key)
{
    int left = _left, right = _right, middle = (_left + _right) / 2 + left;
    if (arr[left] == arr[middle] && arr[middle] == arr[right])    //如果 arr[left] == arr[middle] && arr[right] == arr[middle] 此时不能确定左是单增还是右是单增
    {
        Inorder(arr, left, right, key);
    }
    else if (arr[left] <= arr[middle])    //前半部分为单增区间
    {
        if (key >= arr[left] && key <= arr[middle]) //如果key落在了前半部分则使用折半查找法
        {
            return BinarySearch(arr, left, middle, key);
        }
        else
        {
            return RotateArray(arr, middle + 1, right, key);
        }
    }
    else    //后半部分为单增区间
    {
        if (key > arr[middle] && key <= arr[right])
        {
            return BinarySearch(arr, middle+1, right, key);
        }
        else
        {
            return RotateArray(arr, left, middle, key);
        }
    }
}

 

 

 

 

 

 

3.找出一个排序数组中的 K 出现的次数

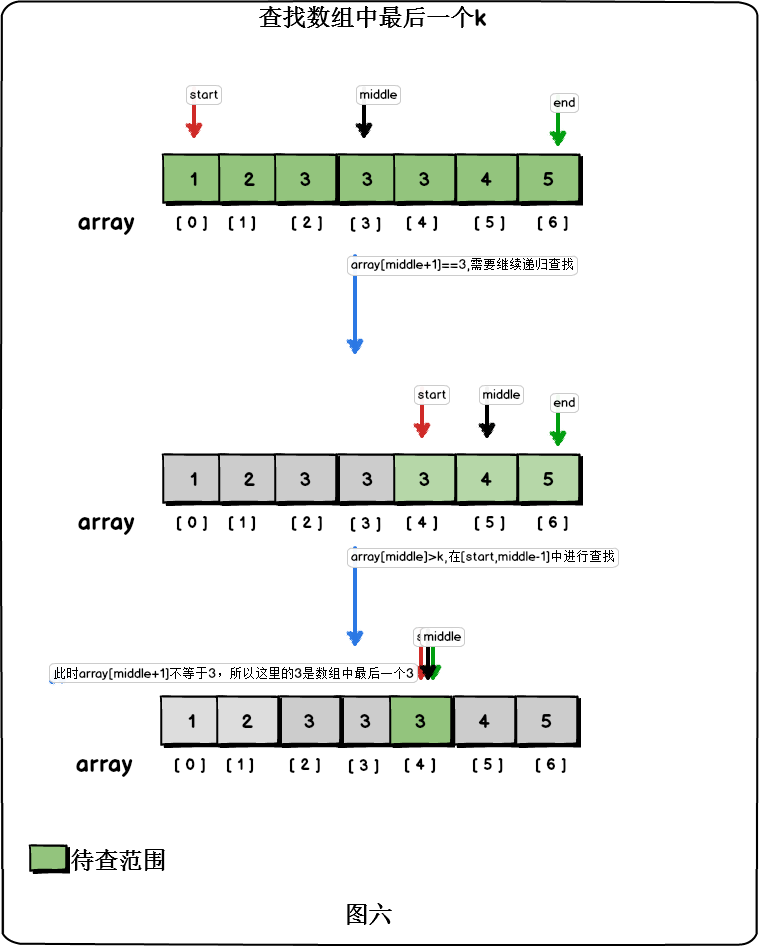
解决思路：假设我们是统计数字k在排序数组中出现的次数，只要找出排序数组中第一个k与最后一个k的下标，就能够计算出k的出现次数。
寻找第一个k时，利用二分查找的思想，我们总是拿k与数组的中间元素进行比较。如果中间元素比k大，那么第一个k只有可能出现在数组的前半段；如果中间元素等于k，我们就需要判断k是否是前半段的第一个k，如果k前面的元素不等于k，那么说明这是第一个k；如果k前面的元素依旧是k，那么说明第一个k在数组的前半段中，我们要继续递归查找。   同样的思路，我们在数组中寻找最后一个k，如果中间元素比K大，那么k只能出现在数组的后半段；如果中间元素比K小，那么K只能出现在数组的前半段。如果中间元素等于k，而k后面的元素等于k，那么最后一个k只能在后半段出现；否则k为数组中最后的一个k。

 

/*排序数组中的K出现的次数*/
int GetFirstK(int* arr, size_t size, int value)
{
    assert(arr);
    int start = 0,middle, end = size - 1;
    while (start <= end)
    {
        middle = (end - start) / 2 + start;
        if (arr[middle]>value)
            end = middle - 1;
        else if (arr[middle] < value)
            start = middle + 1;
        else
        {
            if (middle - 1 >= 0 && arr[middle - 1] == value)
                end = middle - 1;
            else
                return middle;
        }
    }
    return -1;
}





int GetLastK(int* arr, size_t size, int value)
{
    assert(arr);
    int start = 0, middle, end = size - 1;
    while (start <= end)
    {
        middle = (end - start) / 2 + start;
        if (arr[middle]>value)
            end = middle - 1;
        else if (arr[middle] < value)
            start = middle + 1;
        else
        {
            if (middle + 1 < size && arr[middle + 1] == value)
                start = middle + 1;
            else
                return middle;
        }
    }
    return -1;
}



int GetNumberOfK(int* arr, int size, int value)
{
    if (arr == NULL || size <= 0)
        return -1;
    int First = GetFirstK(arr, size, value);
    int Last = GetLastK(arr, size, value);
    if (First >= 0)    // 说明value一定存在
        return (Last - First + 1);
}