冰雹猜想或角谷定理

㈠什么是冰雹猜想？

冰雹猜想是指：一个正整数x，如果是奇数就乘以3再加1，如果是偶数就析出偶数因数2ⁿ，这样经过若干个次数，最终回到1。

 

无论这个过程中的数值如何庞大，就像瀑布一样迅速坠落。而其他的数字即使不是如此，在经过若干次的变换之后也必然会到纯偶数：16-8-4-2-1的循环。

据日本和美国的数学家攻关研究，在小于7*10^11的所有的正整数，都符合这个规律。

 

㈡用JavaScript编写程序代码

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>冰雹猜想或者角古定理</title>
</head>
<body>
<script>
    var x=parseInt(prompt("输入一个正整数"));
    while(x != 1){
        if(x%2 == 0){
            x = x/2;//如果是偶数就析出偶数因数2ⁿ
        }
        else{
            x = x*3+1;//如果是奇数就乘以3再加1
        }
    document.write(x+"<br>");
    }
</script>
</body>
</html>

 

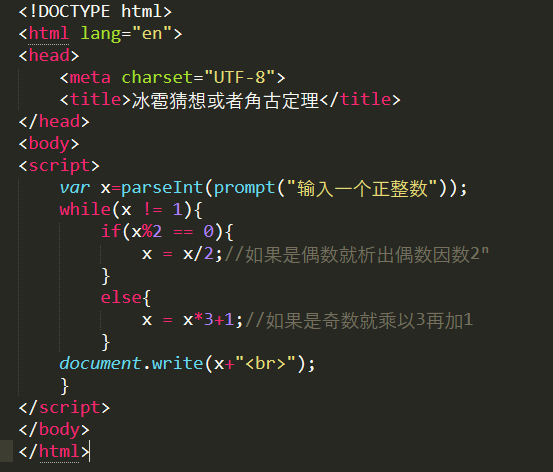
 示例：输入9☟                       输入90☟

                             

 

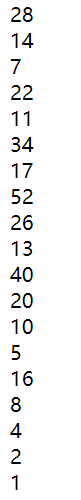
㈢强悍的27

⑴用27按照上述方法进行运算，则它的上浮下沉异常剧烈：首先，27要经过77步骤的变换到达顶峰值9232，然后又经过34步骤到达谷底值1。
 
⑵全部的变换过程（称作“雹程”）需要111步，其顶峰值9232，达到了原有数字27的342倍多；
 
⑶如果以瀑布般的直线下落（2的N次方）来比较，则具有同样雹程的数字N要达到2的111次方。
 
⑷但是在1到100的范围内，像27这样的剧烈波动是没有的（54等27的2的次方倍数的数除外。）

 

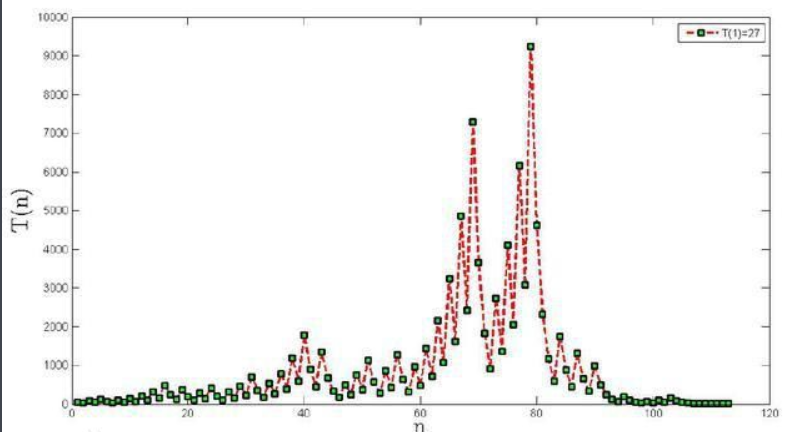
如图所示：27的归一步数要经过多次剧烈波动的奇偶变换，其路径呈不光滑锯齿

posted @ 2019-12-04 20:39  石海莹  阅读(1319)  评论(0)  编辑  收藏  举报