Java刷题笔记

能用StringBuffer的时候坚决不要用String,因为前者的时间和空间效率都更高.

牛顿法求平方根:随便找一个K,然后不断让 k=(k+x/k)/2;直到K的平方与x之间的差距小于限定值.

斐波那契数列用动态规划(也就是写一个数组,一个一个的向后求,最简单).

list的equals是重写过的方法,可以直接使用.

将点的层次遍历算法:

public class LevelOrderBottom {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> lists = new ArrayList<>();
        func(root, 0, lists);
        return lists;
    }

    public void func(TreeNode root, int level, List<List<Integer>> lists) {
        if (root == null)
            return;
        if (lists.size() <= level) {
            List<Integer> list = new ArrayList<>();
            list.add(root.val);
            lists.add(list);
        } else {
            lists.get(level).add(root.val);
        }
        func(root.left, level + 1, lists);
        func(root.right, level + 1, lists);
    }

}

用BFS找到的第一个叶子节点一定是最浅的那个.这时候的深度就是树的最小深度.

关于异或:

交换律：a ^ b ^ c <=> a ^ c ^ b
任何数于0异或为任何数 0 ^ n => n
相同的数异或为0: n ^ n => 0

java中的栈直接用Stack就好,Java中字符串也可以直接用CharAt()来取值.

求start和end的中间数的时候,不要用(start+end)/2,而是用start+(end-start)/2;因为前面那种会有溢出的风险

Java的队列就是ArrayDeque或者LinkedList.这两个都是双端队列,栈和队列操作都支持

//判断一个自然数是否是质数，只用看从2到根号N是否能整除N  一个合数的最小正因子必小于根号N。
//如果N (N>=2)没有小于等于根号N，大于1的约数，那么N必然是质数。
//假设N不是质数，并且不含有小于等于根号N的约数。因为N是合数，那么N必然可以写成N=p*q，并且p和q大于1，p和q都大于根号N。那么p*q>N，矛盾！！

西元前250年，希腊数学家厄拉多塞(Eeatosthese)想到了一个非常美妙的质数筛法，减少了逐一检查每个数的的步骤，可以比较简单的从一大堆数字之中，筛选出质数来，这方法被称作厄拉多塞筛法(Sieve of Eeatosthese)。

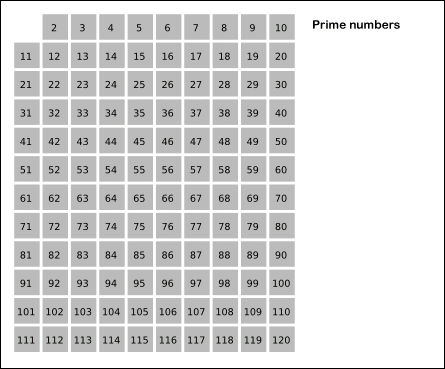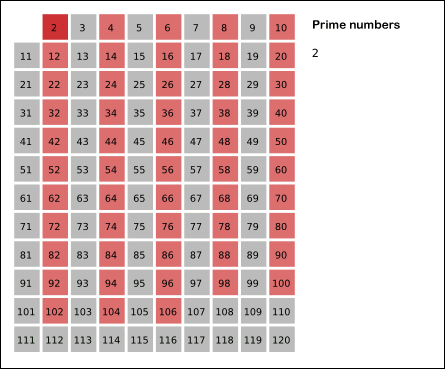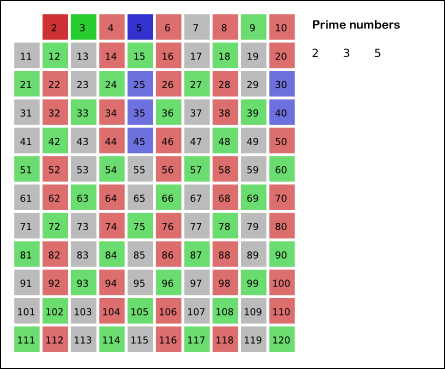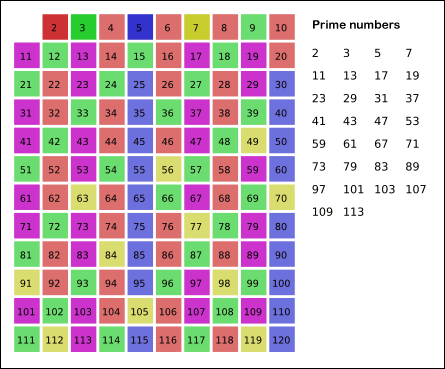
具体操作：先将 2~n 的各个数放入表中，然后在2的上面画一个圆圈，然后划去2的其他倍数；第一个既未画圈又没有被划去的数是3，将它画圈，再划去3的其他倍数；现在既未画圈又没有被划去的第一个数是5，将它画圈，并划去5的其他倍数……依次类推，一直到所有小于或等于 n 的各数都画了圈或划去为止。这时，表中画了圈的以及未划去的那些数正好就是小于 n 的素数。

其实，当你要画圈的素数的平方大于 n 时，那么后面没有划去的数都是素数，就不用继续判了。如下图：

多多使用动态规划的方法很重要,动态规划比递归要好使很多.

用双端队列Deque时,队列方法,add,poll,peek, 是first出队, Last进队.

当用栈方法时, push(),是first进栈, pop()是first出栈.

//二叉树寻找最小公共祖先
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        /**
        注意p,q必然存在树内, 且所有节点的值唯一!!!
        递归思想, 对以root为根的(子)树进行查找p和q, 如果root == null || p || q 直接返回root
        表示对于当前树的查找已经完毕, 否则对左右子树进行查找, 根据左右子树的返回值判断:
        1. 左右子树的返回值都不为null, 由于值唯一左右子树的返回值就是p和q, 此时root为LCA
        2. 如果左右子树返回值只有一个不为null, 说明只有p和q存在与左或右子树中, 最先找到的那个节点为LCA
        3. 左右子树返回值均为null, p和q均不在树中, 返回null
        **/
        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left == null && right == null) return null;
        else if(left != null && right != null) return root;
        else return left == null ? right : left;
    }
}

//二叉排序树寻找最小公共祖先
class Solution {
    TreeNode res = null;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        
        lca(root, p , q);
        return res;
    }
    
    public void lca(TreeNode root, TreeNode p , TreeNode q){
        if((root.val - p.val)*(root.val - q.val) <= 0){
            res = root;
        }else if(root.val < p.val && root.val < q.val){
            lca(root.right, p , q);
        }else{
            lca(root.left, p , q);
        }
    }
}

求一个数的因数,就是从2到该数的平方根,挨个试.

String.split()方法里面是正则表达式,用特殊符号不要忘记加转义符而且要两个\,还有如果有多种分割的话,用中括号括起来就好,不要有空格.中括号里的符号不用转义了.

牛顿法求一个数的平方根和立方根:

平方根迭代公式：a(n+1)=( a(n) + num/a(n) )/2，a(0) 初始化为1

立方根迭代公式：a(n+1)=( 2a(n) + num/( (a(n))^2 ) )/3，a(0) 初始化为1；

#include<iostream>
#include<iomanip>
#define E 0.0001
using namespace std;

double getSqrtRoot(double num) //平方根计算函数
{
    double x0=1, x1;
    x1 = (x0 + num / x0) / 2.0;
    while (fabs(x1 - x0) >= E)
    {
        x0 = x1;
        x1 = (x0 + num / x0) / 2.0;
    }
    return x1;

}

double getCubeRoot(double num) //立方根计算函数
{
    double x0, x1;
    x0 = num;
    x1 = (2 * x0 / 3) + (num / (3 * x0*x0));
    while ((x1 - x0>E) || (x1 - x0<-E))
    {
        x0 = x1;
        x1 = (2 * x0 / 3) + (num / (3 * x0*x0));
    }
    return x1;
}

int main()
{
    double in;
    while (cin >> in)
    {
        cout << fixed << showpoint << setprecision(1) << getCubeRoot(in) << endl;
        cout << fixed << showpoint << setprecision(1) << getSqrtRoot(in) << endl;
    }
    return 0;
}

字符串的substring后面那个坐标可以是最大值加一,也就是越界一个没什么问题的.

String.isEmpty()不能对null进行判断

binarySearch是Arrays的静态方法,第一个参数是数组,第二个参数是要找的数

动态规划是一种很重要的思维,一定要记住啊.加油加油

Java的位运算

1.^(亦或运算) ，针对二进制，相同的为0，不同的为1

public static void main(String[] args) {
 System.out.println("2^3运算的结果是 :"+(2^3));
 //打印的结果是:   2^3运算的结果是 :1
}

2 =======>0010

3 =======>0011

2^3就为0001，结果就是1

2.&（与运算） 针对二进制，只要有一个为0，就为0

还是上述的例子

public static void main(String[] args) {
System.out.println("2&3运算的结果是 :"+(2&3));
//打印的结果是: 2&3运算的结果是 :2
}

3.<<(向左位移) 针对二进制，转换成二进制后向左移动3位，后面用0补齐

public static void main(String[] args) {
System.out.println("2<<3运算的结果是 :"+(2<<3));
//打印的结果是: 2<<3运算的结果是 :16
}

4.>>(向右位移) 针对二进制，转换成二进制后向右移动3位，

public static void main(String[] args) {
System.out.println("2>>3运算的结果是 :"+(2>>3));
//打印的结果是: 2>>3运算的结果是 :0
}

5.>>>(无符号右移) 无符号右移，忽略符号位，空位都以0补齐

10进制转二进制的时候，因为二进制数一般分8位、 16位、32位以及64位表示一个十进制数，所以在转换过程中，最高位会补零。

在计算机中负数采用二进制的补码表示，10进制转为二进制得到的是源码，将源码按位取反得到的是反码，反码加1得到补码

二进制的最高位是符号位，0表示正，1表示负。

>>>与>>唯一的不同是它无论原来的最左边是什么数，统统都用0填充。
——比如，byte是8位的，-1表示为byte型是11111111(补码表示法）
b>>>4就是无符号右移4位，即00001111，这样结果就是15。

牛客网的输入数字要用nextInt()同时来处理.
字符串用nextLine()来处理.多组数据的话要用hasnext来进行判断.
StringBuilder 是线程不安全的,StringBuffer是线程安全的,因此StringBuilder速度更快.
RuntimeException可以不处理,但是Exception必须处理.
Mysql中判断是否为空用 is null，不要用=null。

判断是否是平方数

利用 1+3+5+7+9+…+(2n-1)=n^2，即完全平方数肯定是前n个连续奇数的和
2的幂一定是二进制只有一个1,剩下都是0;
不用加法做相加:
两个整数a, b; a ^ b是无进位的相加； a&b得到每一位的进位；让无进位相加的结果与进位不断的异或，直到进位为0；
两个相同的数异或的话会得0；

String.format()请看这里

刷题非常有用的几个知识点

正则表达式,处理字符串使用
String.format()静态方法,能够省不少事
NumberFormat 处理数字的格式. SimpleDateFormat 处理日期格式.

posted @ 2019-11-24 15:58 时光轻轻吹阅读(718) 评论(0) 编辑收藏举报

刷新页面返回顶部