网络流最大流最小割相关
吃饱了撑的去开了一下网络流从入门到入土的题单
简单在这里整理一下学到的建模小知识
(目前只整理了最大流最小割相关,费用流过会儿在说)
模板
首先先放一个板子在这里
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define mid (l+r)/2
#define INF 1e18
#define N 1005
#define M 2000005
using namespace std;
int n,m,s,t,dep[N],cur[N],Ans=0;
int to[M],val[M],nxt[M],head[N],cnt=1;
void add_edge(int x,int y,int z){
to[++cnt]=y;val[cnt]=z;nxt[cnt]=head[x];head[x]=cnt;
to[++cnt]=x;val[cnt]=0;nxt[cnt]=head[y];head[y]=cnt;
}
queue<int>que;
bool bfs(){
memset(dep,0,sizeof(dep));
que.push(s);dep[s]=1;
while(!que.empty()){
int nw=que.front();que.pop();cur[nw]=head[nw];
for(int i=head[nw];i;i=nxt[i])
if(val[i]&&!dep[to[i]]){
dep[to[i]]=dep[nw]+1;
que.push(to[i]);
}
}
if(!dep[t])return 0;
return 1;
}
int dfs(int nw,int v){
if(nw==t)return v;
int sum=0;
for(int &i=cur[nw];i;i=nxt[i]){
if(dep[to[i]]==dep[nw]+1){
int tmp=dfs(to[i],min(val[i],v));
v-=tmp;sum+=tmp;val[i]-=tmp;val[i^1]+=tmp;
}
if(v==0)return sum;
}
if(!sum)dep[nw]=0;
return sum;
}
int dinic(int &Ans){
while(bfs())Ans+=dfs(s,INF);
return Ans;
}
void init(){memset(head,0,sizeof(head));cnt=1;Ans=0;}
signed main() {
}
拆点
网络流建模中最常用的操作
用于有点权(即一个点中不能使用多次的情况)
具体操作为把每个点拆成 \(i_x\) 和 \(i_y\) 两个点,给 \(i_x\) 和 \(i_y\) 连一条边权为 \(v_i\) 的边
对于原图上的每一条边 \(i \Rightarrow j\) , 给 \(i_y\) 和 \(j_x\) 连边,边权一般为 \(INF\) ,原图有边权限制的话就按图上边权来
例题很多,比如洛谷P1345(这个题是最基础的拆点,点权都为1),洛谷P1231(这个题由于每本书只能用一次所以跑网络流要拆点)
分组
有那么一些图
会给你若干个限制条件使得一些点不能同时选
经过一系列的 瞎猜 证明,一般可以发现不能同时选的点往往在某个性质上必然相异
于是就可以把它转化成 \(n\) 分图
然后左边连 \(S\) 右边连 \(T\) 跑最大流就可以了
需要注意的是大多数情况下每个点只能选一次,所以 \(n > 2\) 时要用到上面的拆点技巧(说的就是上边的第二道例题)
网格图
这个东西和网络流相性不错,不少网络流题的表现形式都是网格图
基本没什么太多技巧,除了别忘建双向边之外也不太容易错
提到这个的主要原因是在网格图上Dinic的复杂度超级优秀,可以跑 \(n=1e6,m=6e6\) 的情况
例题:洛谷P4001(就是这个题,有 \(1e6\) 个点网络流跑的飞快),洛谷P2598
计算几何
有些丧心病狂的题目会把计算几何和网络流出到一起
所以这里补充一点计算几何小知识
点到直线的距离:
在直线上随意找两个点 \(x\) , \(y\),设原来的点为点 \(p\) ,叉乘一下向量 \(p\Rightarrow x\) 和向量 \(y\Rightarrow x\) ,将绝对值再除以 \(x\) 和 \(y\) 的距离就可以了
叉乘的公式 \(x_x*y_y-x_y*y_x\)
点乘的公式 \(x_x*y_x+x_y*y_y\)
例题:洛谷P4048
最大权闭合子图
这是网络流中一个非常有趣的问题
例题长成这样:(出处:洛谷P2672)
W 教授正在为国家航天中心计划一系列的太空飞行。每次太空飞行可进行一系列商业性实验而获取利润。现已确定了一个可供选择的实验集合 $ E = { E_1, E_2, \cdots, E_m } $,和进行这些实验需要使用的全部仪器的集合 $ I = { I_1, I_2, \cdots, I_n } $。实验 $ E_j $ 需要用到的仪器是 $ I $ 的子集 $ R_j \subseteq I $。
配置仪器 $ I_k $ 的费用为 $ c_k $ 美元。实验 $ E_j $ 的赞助商已同意为该实验结果支付 $ p_j $ 美元。W 教授的任务是找出一个有效算法,确定在一次太空飞行中要进行哪些实验并因此而配置哪些仪器才能使太空飞行的净收益最大。这里净收益是指进行实验所获得的全部收入与配置仪器的全部费用的差额。
对于给定的实验和仪器配置情况,编程找出净收益最大的试验计划。
对于这类题,我们的做法是:让 \(S\) 与所有的正权点相连,所有的负权点与 \(T\) 相连,对于原图中的所属关系根据是否可以付出代价不选连一条权值为 \(INF/val\) 的边,然后跑最小割(最大流),答案就是正权和减去最小割。
举个例子,对于这道题,我们可以这么画图
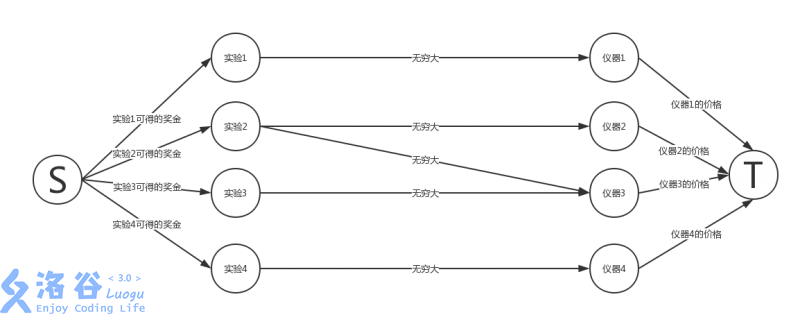
(这图是贺的)
简单口胡一下正确性
首先最大流等于最小割
由于中间的边无穷大我们不需要考虑这些边,只要考虑割掉的是实验奖金还是仪器费用就好了
如果割掉的是实验奖金,那么最终的最小割里就算入了这个实验的奖金,等于说没做
如果割掉的是仪器费用,那么最终的最小割里就算入了仪器费用,等于说购买了这些仪器
所以显然这是可行的
最优性的话,根据上面的 感性理解 证明我们已经知道了答案是正权和减去图的一个割,那么显然最小割最优
最小割
这个其实应该放在前面但是没有关系
首先最小割在数值上是等于最大流的,并且在跑最大流时可以求出最小割的一种方案
具体来说就是从 \(S\) 开始dfs,只走 \(val>0\) 的边,所有碰到的 \(val_i=0\) 的边就是被割掉的边
最小割的最小边数
这个问题非常简单,考虑在跑最小割时把每条边的边权赋值成 \(w*T+1\) (\(T\) 为极大值)
再跑出最小割后,原来的最小割就是 \(ans/T\) , 边数就是 \(ans\mod T\)
最小割的可行边 \((x,y)\)
首先显然这得是条满流边,否则肯定有更优的
其次 \(x\) 在残量网络中不连通 \(y\),否则割了这条边也没用
最小割的必需边 \((x,y)\)
首先这依然得是条满流边
其次残量网络中 \(S\) 与 \(x\) 连通 ,\(y\) 与 \(T\) 连通
这样的话如果不割这条边 \(S\) 与 \(T\) 就连通了,所以必须割这一条
快速判断每条边是否是可行边或者必需边
我们可以先跑一遍dinic,再求一遍强联通分量(只能走残量网络)
对于可行边,两个端点不在同一个强联通分量内即可
对于必需边,两个端点分别和 \(S\) 或 \(T\) 在同一个强联通分量内即可
(当然都要满足满流条件哦)
简单解释一下,首先对于一条满流边 \((x,y)\) ,残量网络上必然有边 \((y,x)\) (网络流的反向边)
因此如果 \(x\) 可以到 \(y\) ,那么必然形成一个环,因此对于一条满流边,两个端点不在同一个强联通分量内是可行边的充要条件
而如果两个端点分别和 \(S\) 或 \(T\) 在同一个强联通分量内,就相当于残量网络中两个端点分别于 \(S\) , \(T\) 连通
所以这是必需边的充要条件
例题:洛谷P4126
退流
在一些网络流的题目中,我们会遇到这样一类问题:跑完网络流之后,要加减一丢丢边,然后问你最大流(最大费用)。
如果因为这一丢丢的改动就去重新建图跑一遍的话,时间复杂度会高的离谱。
我们发现,如果是加边的话,可以直接加进去然后直接在原来跑完的基础上继续跑,而难处理的是减边。
这个时候我们就用到优秀的退流啦!假设源点和汇点是 \(S\) 和 \(T\),要删去一条边 \(( u , v )\),那么我们只需要以 \(u\) 为源点,向 \(S\) 跑一次最大流,然后再以 \(T\) 为源点,向 \(v\) 跑一次最大流即可。最后将 \(( u , v )\) 这条边以及其反向边的流量设为 \(0\) 即可。
你可能会问:\(u\) 向 \(S\) 跑最大流时,流过去的流量可能比原来 \(S\) 流到 \(u\) 的更多啊?
这个不用担心,网络流有反向边嘛~优秀的反悔机制会解决这个问题的。换句话说,这样的操作不会使得 \(S\) 能往 \(T\) 流更多流量,或者使原本能不经过 \(( u , v )\) 流过去的流量而流不到。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号