2021年9月(甲级)秋季PAT考试
记录2021.9.12
终于考完了。92分,已经超出了我自己的预期成绩了,很开心。(弱弱的说,我考试前做PAT前几年的仿真模拟卷都没有上70的,最高60多分,虽然说这次应该算是这几年以来最简单的一次了吧,所以说考试前其实我是没啥信心的QAQ,可能对于大佬来说92仅此而已,但是对我来说是莫大的惊喜了,开始没几分钟点进去,就有大佬已经AC了,瑟瑟发抖~~)
因为准备考研浙大才准备的PAT甲级考试,但是考试前刚刚听说软工免推的PAT成绩不能抵机试了,所以这次考试压力也没有多大。
我是非科班出身的,只是大一的时候有上过C语言,C++的相关课程,但都是水过去的。所以基本上到了大三还是不会打代码的小菜鸡一枚,为了准备考PAT也在图书馆借了算法笔记,收藏了柳婼大神的博客,看了很多的经验贴。我大概是七月中旬开始准备的,那时候拿这算法笔记啃,感觉刚开始还是很吃力的,一道排序题就可以难住我好几个小时,后来渐渐上手后,特别是学习了第六章的C++中的STL容器,感觉好用的飞起,明明可以很轻松的写代码,之前一直都在用土本法。但是这也算是一种经历吧,没有土办法一点点的写过,就不知道STL容器有多好用。到了八月份的时候,算法笔记才啃了不到一半,其实有点慌张了,大概是从八月中旬开始,就把每天大部分的时间往PAT上倾斜,emmm...大家不要学我,能尽早开始就不要偷懒,我就是懒惯了,才导致后面时间来不及。大概是到9月份初的时候,其实我才把算法笔记学习完,当然动态规划,后面字符串提升什么的没学,毕竟没时间了嘛,然后我就开始从后往前刷题库,四道题四道题刷,看柳婼大神的代码,但是由于柳婼大神的代码是只有分析的,虽然讲的很简介明了,但是一般对于我们这种代码打的少的人来说,其实不太容易想得到,所以我是把b站的讲PAT甲级的up主弄夫的视频和柳婼大神的代码结合着学习的,从中其实也学习到了非常多STL容器的具体用法,其实算法笔记中虽然是讲的较为详细了,但是你用的太少还是不会用的,我觉得看别人的代码看多了,自己自然而然的就用上了这些好用的方法,而不是纠结着一定要用自己写出来的,我觉得就9月初一直到考试前,我自己结合大神的代码视频刷题学习的过程是我提升最快的时候,算法笔记只是给了你一个门槛,让你懂得了该如何应对PAT上不同的题目,学习了各种算法(我真的是小白,之前从来没用过这些算法)真的如大佬所言,就算是对于小白也是很友好的。不过想要有所提升,算法笔记明显不够用,在学习完算法笔记的基础上,刷题总结学习大佬的代码,思维方式才是备考的重中之重。
讲一下这次考试的心路历程,感觉看题是杠杠的重要的。刚开始做题的时候,我把所有的题目都看了一遍,大概看了一下要考啥,因为是英语(我的英语真一般,稍微来一点不常见的单词就会不认识)所以读题较慢。大概4道题读了10分钟,而且是粗粗的读,根本没有读懂,就大概感觉第一题读不懂,第二题好像考栈,第三题考图论,第四题考堆?树(刚开始是这样想的),然后读完题我就去看了一下提交通过率,好家伙,第一题的通过率低的离谱,反而是第四题最高,然后我就转向第四题的怀抱了,但是读了半天,也读不懂题目,又是堆啊,又是中序遍历啥的,然后我就想,难道和之前的一样是考建堆吗,只不过这个是小顶堆,然后我就按照堆的思路做下去(考前打过好几遍相关代码了,所以还是挺熟的),然后写到向上调整的时候发现,好像我看到那张样例图给的不是完全二叉树啊,这咋整,然后给我整愣住了,我又看了一下题目,发现没啥思路。
这时候大概还有2个半小时,然后我就又去看了一下通过率,咋第二题的通过率这么高呢?我之前粗粗的看了一下第二题,其实也没读懂题目,然后我就去在仔细读了一遍题目,发现的真的挺简单的,只要稍微排序一下,然后用STL中的stack容器每次压出一个帽子的size(我用的是unordered-map的两个映射)就在映射中找到体重对应的位置下标输出即可。很快20分钟不到读题和做题就结束了,这时候还有2个小时十几分钟,然后我就想好歹20分了,没有被0封,心情不错,就又去看通过率(呵呵,没错我就是看通过率做题的,其实效果还不错,但是其实并不是通过率低的题目就一定难的,我我最后写第一题的时候也就不到半个小时,通过率低说不定是里面有坑,所以很多大佬没有拿到满分),发现还是第四题较高,又跑去攻克第四题。这次仔细看了一下他给我的例子,那个pair,和图,发现根据小的数字的堆顶就是小顶堆的特性,但是看他给出的好像key的顺序好像是从小到大的,又看图,发现很像题库中做的一道建立笛卡尔树的题目(就是每次从中序中选择最小的数作为根节点,依据这个来建树,这道题我考试前因为在背代码段,所以也打过好几遍了),所以发现这根本不是建堆,他只是有一点堆的特性,所以只需要把这个key和priority作为一个结构体一起排序,当然是按照key的值的从小到大排序了,然后把他们看成一个整体,每次在结构体数组中找到priority最小的值,然后然这个值作为根结点,递归建树,最后层序遍历一下就okk啦~,写法之后一步AC,很开心。(现在看了一下觉得priority这个单词好眼熟,想起了priority_queue所以这道题优先队列应该更好做)
这时候大概还有1个小时30多分钟,我就想,就剩两题了,还能给我难住不成,然后我就开始做第三题,毕竟第一题通过率很低,而且我之前看了题目,确实不太读的懂(提示没看),看了之后,也是很快有了思路,大概意思就是给你一张图,让你选择从哪个顶点出发可以遍历到最多的顶点(访问过的顶点不能再访问),虽然我后来看到有人的群里说每次要选择编号最小的点走,但是很奇怪的是,我由于没有看到这句话,所以就是用了个dfs,进行深度遍历,记录遍历的深度(即过一个顶点要让深度+1,当然要回溯的,回来之后还要-1)直到没有顶点可以走的时候就退出循环,哎,也是我太蠢了,没有真正搞懂递归,虽然想法很简单,但是现实很骨感啊,我发现无论我怎么做,我都导不出最后到达递归边界的时候我想要的深度值,然后我就想debug吧,看一下出了什么问题,然后遇到了最让我奔溃的事情,那个考点的Dev-C++是没有办法debug的,啊真想当场哭出来,由于我的电脑上之前也试过VS,但是不知道咋的就是用不了VS来运行C,所以我用的都是Dev-C,让我当场去研究VS也不现实,那我只能cout打印看情况了呀,但是有错的地方又在递归函数内部,搞的我头晕,我后来就发现了,好像是因为函数内部的参数是个复制的参数,改变不了主函数的参数值的,然后我就想,有啥大不了的,用引用类型呗,然后发现不得行,报错(也可能是我写的有问题),然后我就想,这样也不行那就全局变量,然后发现,全局变量也不得行,因为我写的dfs是有回溯的,每次回溯回来就回到原值了,根本带回不了最深层的深度的值,经过一次次的尝试和失败,我突然想起了之前在算法笔记上,用Dijkstra+DFS求最优解的时候,算法笔记上教我们的是在最深层的时候(就是到达递归边界的时候)把想要的最大值赋值给全局变量,就可以带回这个值了,然后我就这样做了一下,果然AC了。(但是由于我是没有看到其他大佬说的那句每次选择往最小的点走的,所以我也还不太清楚为什么对),这时候由于在第三题耗费了太多时间了,没有debug呜呜呜,可恶。
第一题只剩下30分钟了,我再次强调读题真的很重要,读好题目事半功倍,我读题大概读了15分钟,才搞懂什么意思,(也是刚看时看题目的时候没有看到下面的提示,耗费了几分钟的时间),然后就剩10多分钟了,我就着急的,代码打的很快,不到五分钟就大概打好了,当然中间有些错误,因为没有想太多就打了,根本没时间,所以没有想到什么方法就用了什么。中间改错cout查看了一下,然后最后一分钟改出来12分。这里说一下,由于我之前太急了,其实感觉这道题能过的希望也不大,所以我设数组设置了一个100大小的数组,所以虽然最后过了,但是从第三个点开始就段错误了,段错误的很明显,谁叫我之前着急,设置了100大小的数组呢,哎,当然说这些为时已晚了。
这仅仅是我的一次考试体验,以此记录。当然觉得自己挺幸运的,碰上的这次考试这么简单,不像前几次的卷子,我看到题目没有丝毫的想法。顺便膜拜一下大佬们,TQL。
代码
- 7-1 Arrays and Linked Lists (20 分)
Let's design a data structure A that combines arrays and linked lists as the following:
At the very beginning, an integer array A0 of length L0 is initialized for the user. When the user tries to access the ith element A[i], if 0≤i<L0, then A[i] is just A0[i]. Now our system is supposed to return h0+i×sizeof(int)as the accessed address, where h0 is the initial address of A0, and sizeof(int) is the size of the array element, which is simply int, taking 4 bytes.
In case there is an overflow of the user's access (that is, i≥L0), our system will declare another array A1 of length L1. Now A[i] corresponds to A1[j] (It's your job to figure out the relationship between i and j). If 0≤j<L1, then h1+j×sizeof(int) is returned as the accessed address, where h1 is the initial address of A1.
And if there is yet another overflow of the user's access to A1[j], our system will declare another array A2 of length L2, and so on so forth.
Your job is to implement this data structure and to return the address of any access.
Input Specification:
Each input file contains one test case. For each case, the first line gives 2 positive integers N (≤104) and K (≤103) which are the number of arrays that can be used, and the number of user queries, respectively.
Then N lines follow, each gives 2 positive integers, which are the initial address (≤107) and the length (≤100) of an array, respectively. The numbers are separated by spaces. It is guaranteed that there is no overlap of the spaces occupied by these arrays.
Finally, K indices of the elements queried by users are given in the last line. Each index is an integer in the range [0,220].
Output Specification:
For each query, print in a line the accessed address. If the queried index exceeds the range of all the N arrays, output Illegal Access instead, and this query must NOT be processed.
Print in the last line the total number of arrays that have been declared for the whole process.
Sample Input:
6 7
2048 5
128 6
4016 10
1024 7
3072 12
9332 10
2 12 25 50 28 8 39
Sample Output:
2056
4020
1040
Illegal Access
3072
140
3116
5
Hint:
A[2] is just A0[2], so the accessed address is 2048+2×4=2056.
In order to access A[12], declaring A1 is not enough, we need A2 with initial address h2=4016. Since A[12]=A2[1], the accessed address is 4016+1×4=4020.
In order to access A[25], we need A3 with initial address h3=1024. Since A[25]=A3[4], the accessed address is 1024+4×4=1040.
The access of A[50] exceeds the maximum boundary of all the arrays, and hence an illegal access. There is no extra array declared.
In order to access A[28], we need A4 with initial address h4=3072. Since A[28]=A4[0], the accessed address is just 3072.
It is clear to see that A[8]=A1[3] and hence the accessed address is 128+3×4=140; and A[39]=A4[11] so the accessed address is 3072+11×4=3116.
All together there are 5 arrays used for the above queries.
考试时候的代码,只拿了12f,如果不是数组太小段错误的话,就有18f了,其中一个是答案错误,倒是第二个点错误,暂时还没找到
#include<iostream>
#include<cctype>
#include<string>
#include<set>
#include<stack>
#include<unordered_set>
#include<unordered_map>
#include<map>
#include<queue>
#include<algorithm>
#include<cstring>
using namespace std;
int main(){
int n,m;
cin >> n >> m;
int a[100],len[100];
for(int i = 0; i < n; i++){
cin >> a[i] >> len[i];
}
int sum = 0;
int c[100];
for(int i = 0; i < n; i++){
sum += len[i];
c[i] = sum;
}
int maxn = -1;
while(m--){
int b;
cin >> b;
if(b>=c[n-1]) cout<<"Illegal Access" <<endl;
else{
int i;
for( i = 0; i < n; i++){
if(c[i]>b) break;
}
if(b>maxn){
maxn = b;
}
if(i==0)cout << a[i] + 4 * b<<endl;
if(i!=0)cout << a[i] + 4 *(b-c[i-1])<<endl;
}
}
int i;
for(i = 0; i < n; i++){
if(c[i]>=maxn) break;
}
cout << i+1;
return 0;
}
7-2 Stack of Hats (25 分)
PATers believe that wearing hats makes them look handsome, so wherever they go, everyone of them would wear a hat. One day they came to a restaurant, a waiter collected their hats and piled them up. But then when they were ready to leave, they had to face a stack of hats as shown by the above figure. So your job is to help them line up so that everyone can pick up his/her hat one by one in order without any trouble.
It is known that every hat has a unique size, which is related to the weight of its owner -- that is, the heavier one wears larger hat.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive number N (≤104) which is the number of PATers. The next line gives N distinct sizes of the hats, which are positive numbers no more than 105. The sizes correspond to the hats from bottom up on the stack. Finally in the last line, N distinct weights are given, correspond to the hat owners numbered from 1 to N. The weights are positive numbers no more than 106. All the numbers in a line are separated by spaces.
Output Specification:
For each test case, print in a line the indices of the hat owners in the order of picking up their hats. All the numbers must be separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.
Sample Input:
10
12 19 13 11 15 18 17 14 16 20
67 90 180 98 87 105 76 88 150 124
Sample Output:
3 4 8 6 10 2 1 5 9 7
Hint:
The 1st hat has the largest size 20, hence must correspond to the one with the largest weight, which is the 3rd one of weight 180. So No.3 must go first.
The 2nd hat has the 6th smallest size 16, hence corresponds to the 6th smallest weight, which is 98. So No.4 is the next to go.
And so on so forth.
代码
#include<iostream>
#include<stack>
#include<unordered_map>
#include<algorithm>
using namespace std;
const int maxn = 10001;
int weight[maxn];
int hat[maxn];
bool cmp(int a,int b){
return a > b;
}
int main(){
int n, si, ans = 0;
cin >> n;
unordered_map<int,int> ind, hat_to_weight, weight_to_hat;
stack<int> st;
for(int i = 0; i < n; i++){
scanf("%d",&si);
hat[i]=si;
st.push(si);
}
for(int i = 0; i < n; i++){
scanf("%d",&weight[i]);
ind[weight[i]]= i + 1;//有体重得到下表
}
sort(weight,weight+n,cmp);
sort(hat,hat+n,cmp);
for(int i = 0; i < n; i++){
hat_to_weight[hat[i]]=weight[i];
weight_to_hat[weight[i]]=hat[i];
}
while(!st.empty()){
int nowsize = st.top();
st.pop();
int num = ind[hat_to_weight[nowsize]];
if(ans) cout << ' ';
cout << num;
ans++;
}
return 0;
}
7-3 Playground Exploration (25 分)
A playground is equipped with ball pits and tents connected by tunnels. Kids can crawl through the tunnels to meet their friends at a spot with a tent or a ball pit.
Now let's mark each meeting spot (a tent or a ball pit) by a number. Assume that once a kid starts to explore the playground from any meeting spot, he/she will always choose the next destination with the smallest number, and he/she would never want to visit the same spot twice. Your job is to help the kids to find the best starting spot so they can explore as many spots as they can.
Input Specification:
Each input file contains one test case. For each case, the first line gives two positive integers N (≤100), the total number of spots, and M, the number of tunnels. Then M lines follow, each describes a tunnel by giving the indices of the spots (from 1 to N) at the two ends.
Output Specification:
Print in a line the best starting spot which leads to the maximum number of spots, and the number of spots a kid can explore. If the solution is not unique, output the one with the smallest index. There must be exactly 1 space between the two numbers, and there must be no extra space at the beginning or the end of the line.
Sample Input:
8 10
1 2
3 4
5 8
1 4
6 1
3 7
2 4
5 3
2 8
2 5
Sample Output:
6 7
Hint:
Actually there are two solutions. Kids can either start from 6 and go through 1->2->4->3->5->8, or from 7 to 3->4->1->2->5->8, both can visit 7 spots. Since 6 is a smaller index, we output 6 as the starting spot.
代码
#include<iostream>
#include<set>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = 101;
const int INF = 1000000000;
int G[maxn][maxn];
int n, m;
bool vis[maxn] = {false};
//从一点开始,走过的点要尽可能的多,而且访问过的节点就不能在访问了,求访问能够走到最多的点的起点的下表,并且求出能最多走多少个点,如果路径不唯一,就要走下表最小的那个
int maxdepth = -1;
bool if_can_vis_other(int x){//判断当前结点是否还存在可以继续访问的结点
for(int i = 1; i <= n; i++){
if(G[i][x]!=INF&&vis[i]==false) return true;
}
return false;
}
int mdepth = -1;
void dfs(int index,int depth){
if(if_can_vis_other(index)==false){//已经没有结点可以继续访问了
if(depth>mdepth){
mdepth = depth;
}
return;
}
vis[index]=true;
for(int i = 1; i <= n; i++){
if(vis[i]==false&&G[i][index]!=INF){
dfs(i,depth+1);
}
}
}
int main(){
scanf("%d%d",&n,&m);
fill(G[0],G[0]+maxn*maxn,INF);
for(int i = 0; i < m; i++){
int t1,t2;
scanf("%d%d",&t1,&t2);
G[t1][t2] = G[t2][t1]=1;
}
int maxdepth = -1;
set<int> loc;
for(int i = 1; i <= n; i++){//对于每一个起点,我们都遍历一下,找到数量最大的那个就好了
memset(vis,false,sizeof(vis));//每一个都要重新初始化
vis[i]=true;
mdepth = -1;
dfs(i,1);
if(mdepth>maxdepth){
maxdepth = mdepth;
loc.clear();//如果这个值比最大值还要大更新最大值,并且清空最大值所对应的起点的下标
loc.insert(i);//存入当前地址的下标
}else if(mdepth==maxdepth){
loc.insert(i);//如果最大值一样,都存在set里面,自动排序,最小的就在前面
}
}
auto it = loc.begin();
printf("%d %d",*it,maxdepth);
return 0;
}
7-4 Sorted Cartesian Tree (30 分)
A Sorted Cartesian tree is a tree of (key, priority) pairs. The tree is heap-ordered according to the priority values, and an inorder traversal gives the keys in sorted order. For example, given the pairs { (55, 8), (58, 15), (62, 3), (73, 4), (85, 1), (88, 5), (90, 12), (95, 10), (96, 18), (98, 6) }, the increasing min-heap Cartesian tree is shown by the figure.
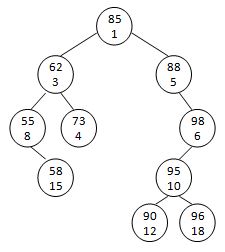
Your job is to do level-order traversals on an increasing min-heap Cartesian tree.
Input Specification:
Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N lines follow, each gives a pair in the format key priority. All the numbers are in the range of int.
Output Specification:
For each test case, print in the first line the level-order traversal key sequence and then in the next line the level-order traversal priority sequence of the min-heap Cartesian tree.
All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.
Sample Input:
10
88 5
58 15
95 10
62 3
55 8
98 6
85 1
90 12
96 18
73 4
Sample Output:
85 62 88 55 73 98 58 95 90 96
1 3 5 8 4 6 15 10 12 18
代码
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
const int INF = 1000000000;
struct node{
int key, priority;
node* lchild,*rchild;
};
struct p{
int key, priority;
}p[31];
bool cmp(struct p a,struct p b){
return a.key < b.key;
}
node* creat(int inL,int inR){
if(inL > inR) return NULL;
int k, MIN = INF;
for(int i = inL; i <= inR; i++){
if(p[i].priority < MIN){
MIN = p[i].priority;
k = i;
}
}
node *root = new node;
root->priority = MIN;
root->key = p[k].key;
root->lchild = creat(inL, k - 1);
root->rchild = creat(k + 1, inR);
return root;
}
vector<int> k, pr;
void leverOrder(node* root){
queue<node*> q;
q.push(root);
while(!q.empty()){
node* cur = q.front();
q.pop();
k.push_back(cur->key);
pr.push_back(cur->priority);
if(cur->lchild!=NULL) q.push(cur->lchild);
if(cur->rchild!=NULL) q.push(cur->rchild);
}
}
int main(){
int n;
cin >> n;
for(int i = 0; i < n; i++){
cin >> p[i].key >> p[i].priority;
}
sort(p,p + n,cmp);
node* root = creat(0, n-1);
leverOrder(root);
for(int i = 0; i < k.size();i++){
if(i) printf(" ");
printf("%d",k[i]);
}
printf("\n");
for(int i = 0; i < pr.size();i++){
if(i) printf(" ");
printf("%d",pr[i]);
}
return 0;
}






