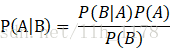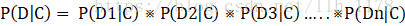数据挖掘相关算法

数据挖掘算法总结

1.分类算法

所谓分类，简单来说，就是根据文本的特征或属性，划分到已有的类别中。常用的分类算法包括：决策树分类法，朴素的贝叶斯分类算法(native Bayesian classifier)、基于支持向量机(SVM)的分类器，神经网络法，k-最近邻法(k-nearest neighbor，kNN)，模糊分类法等等

• 决策树分类法

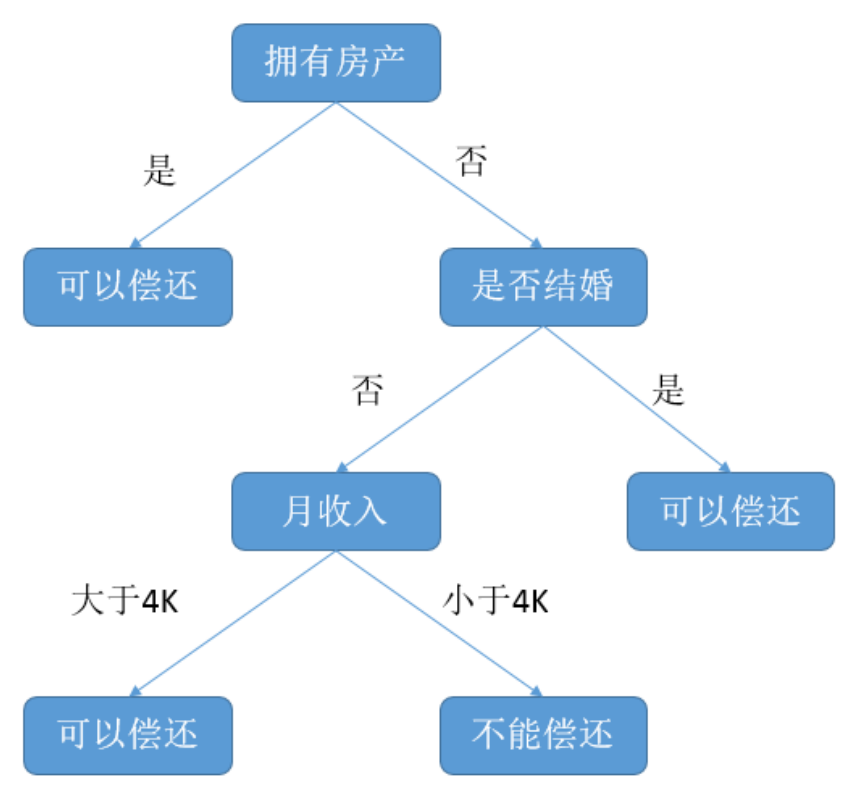
  机器学习中决策树是一个预测模型，它表示对象属性和对象值之间的一种映射，树中的每一个节点表示对象属性的判断条件，其分支表示符合节点条件的对象。树的叶子节点表示对象所属的预测结果。

  

 

• 朴素的贝叶斯分类算法(native Bayesian classifier)

  

  举例说明，我们想计算含有单词drugs的邮件为垃圾邮件的概率。 在这里，A为“这是封垃圾邮件”。我们先来计算P(A)，它也被称为先验概率，计算方法是，统计训练中的垃圾邮件的比例，如果我们的数据集每100封邮件有30封垃圾邮件，P(A)为30/100=0.3。 B表示“该封邮件含有单词drugs”。类似地，我们可以通过计算数据集中含有单词drugs的邮件数P(B)。如果每100封邮件有10封包含有drugs，那么P(B)就为10/100=0.1。 P(B|A)指的是垃圾邮件中含有的单词drugs的概率，计算起来也很容易，如果30封邮件中有6封含有drugs，那么P(B|A)的概率为6/30=0.2。 现在，就可以根据贝叶斯定理计算出P(A|B)，得到含有drugs的邮件为垃圾邮件的概率。把上面的每一项带入前面的贝叶斯公式，得到结果为0.6。这表明如果邮件中含有drugs这个词，那么该邮件为垃圾邮件的概率为60%。其实，通过上面的例子我们可以知道它能计算个体从属于给定类别的概率。因此，他能用来分类。 我们用C表示某种类别，用D代表数据集中的一篇文档，来计算贝叶斯公式所要用到的各种统计量，对于不好计算的，做出朴素假设，简化计算。 P(C)为某一类别的概率，可以从训练集中计算得到。 P(D)为某一文档的概率，它牵扯到很多特征，计算很难，但是，可以这样理解，当在计算文档属于哪一类别时，对于所有类别来说，每一篇文档都是独立重复事件，P(D)相同，因此根本不用计算它。稍后看怎样处理它。 P(D|C)为文档D属于C类的概率，由于D包含很多特征，计算起来很难，这时朴素贝叶斯就派上用场了，我们朴素地假定各个特征是互相独立的，分别计算每个特征（D1、D2、D3等）在给定类别的概率，再求他们的积。

• k-最近邻法(k-nearest neighbor，kNN)

  我之前的博客已经有详细介绍https://www.cnblogs.com/shierlou-123/p/11428651.html

2.聚类算法

• k-means聚类算法我之前已有详细介绍：https://www.cnblogs.com/shierlou-123/p/11428651.html

   

3.回归模型

本小节将介绍五种常见的回归模型的概念及其优缺点，包括线性回归(Linear Regression), 多项式回归(Ploynomial Regression), 岭回归(Ridge Regression)，Lasso回归和弹性回归网络(ElasticNet Regression).

• 线性回归(Linear Regression)

  线性回归的几个特点：

  1. 建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。

  2. 可以根据系数给出每个变量的理解和解释

  3. 对异常值很敏感

• 多项式回归(Ploynomial Regression)

  多项式回归的特点：

  1. 能够拟合非线性可分的数据，更加灵活的处理复杂的关系

  2. 因为需要设置变量的指数，所以它是完全控制要素变量的建模

  3. 需要一些数据的先验知识才能选择最佳指数

  4. 如果指数选择不当容易出现过拟合

• 岭回归(Ridge Regression)

  分析岭回归之前首先要说的一个共线性(collinearity)的概念，共线性是自变量之间存在近似线性的关系，这种情况下就会对回归分析带来很大的影响。因为所分析的X1总是混杂了X2的作用，这样就造成了分析误差，所以回归分析时需要排除高共线性的影响。

  标准线性回归的优化函数如下：

   

  其中X表示特征变量，w表示权重，y表示真实情况。岭回归是针对模型中存在的共线性关系的为变量增加一个小的平方偏差因子(也就是正则项)，可以表示成下面的式子：

   

  这样的平方偏差因子向模型中引入了少量偏差，但大大减少了方差。 领回归的特点:

  1. 领回归的假设和最小平方回归相同，但是在最小平方回归的时候我们假设数据服从高斯分布使用的是极大似然估计(MLE)，在领回归的时候由于添加了偏差因子，即w的先验信息，使用的是极大后验估计(MAP)来得到最终的参数

  2. 没有特征选择功能

• Lasso回归

  Lesso与岭回归非常相似，都是在回归优化函数中增加了一个偏置项以减少共线性的影响，从而减少模型方程。不同的是Lasso回归中使用了绝对值偏差作为正则化项，Lasso回归可以表示成下面的式子：

   

  岭回归和Lasso回归之间的差异可以归结为L1正则和L2正则之间的差异： 内置的特征选择(Built-in feature selection):这是L1范数很有用的一个属性，而L2范数不具有这种特性。因为L1范数倾向于产生系数。例如，模型中有100个系数，但其中只有10个系数是非零系数，也就是说只有这10个变量是有用的，其他90个都是没有用的。而L2范数产生非稀疏系数，所以没有这种属性。因此可以说Lasso回归做了一种参数选择形式，未被选中的特征变量对整体的权重为0。 稀疏性：指矩阵或向量中只有极少个非零系数。L1范数具有产生具有零值或具有很少大系数的非常小值的许多系数的属性。 计算效率：L1范数没有解析解，但L2范数有。这使得L2范数的解可以通过计算得到。L1范数的解具有稀疏性，这使得它可以与稀疏算法一起使用，这使得在计算上更有效率。

• 弹性回归网络(ElasticNet Regression)

  弹性回归网络是Lesso回归和岭回归技术的混合体。它使用了L1和L2正则化，也达到了两种技术共有的效果，弹性回归网络的表达式如下：

   

  在Lasso和岭回归之间进行权衡的一个实际是运行弹性网络在循环的情况下继承岭回归的一些稳定性。 弹性回归网络的优点：

  1. 鼓励在高度相关变量的情况下的群体效应，而不像Lasso那样将其中一些置为0.当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso倾向于随机选择其中一个，而弹性网络倾向于选择两个。

  2. 对所选变量的数量没有限制。

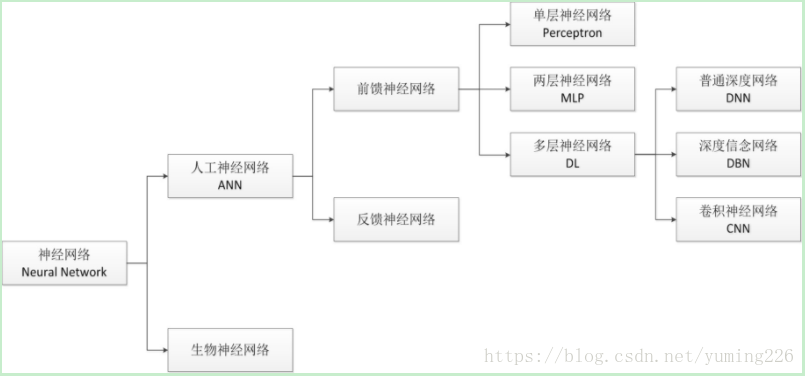
4.神经网络

 

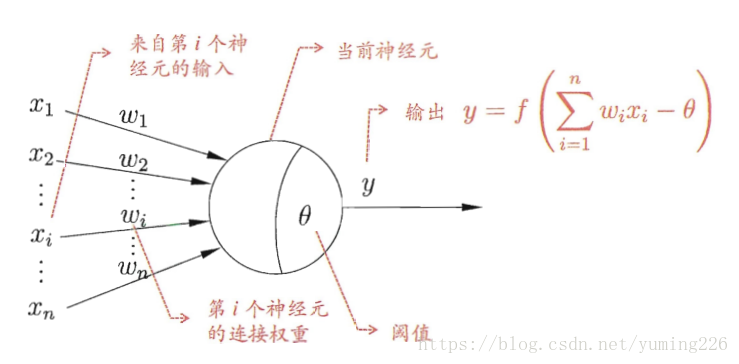
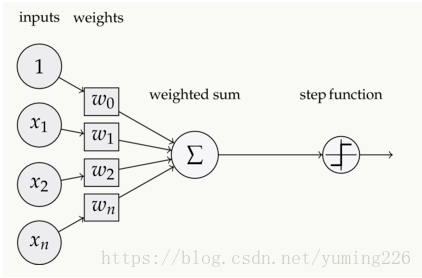
• 激活函数

如下图，在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

 

 

参考链接：https://blog.csdn.net/llh_1178/article/details/79848922

　　　　    https://blog.csdn.net/u013181595/article/details/80517537