四元数的笔记

定义

四元数　\(h = a + bi + cj + dk\)

共轭:　$ h^* = a -bi -cj -dk$

逆：　$ h^{-1} = \frac{h^*}{|h|2}$

所以单位四元数的共轭等于他的逆

单位四元数（绝对值为1的四元数）若实部为cos(t),它的共轭作用是一个角度为2t的转动，转轴为虚部的方向。

四元数的优点是：

• 表达式无奇点,无万向锁（和例如欧拉角之类的表示相比）
• 比矩阵更简炼,旋转矩阵有９个变量（也更快速）
• 单位四元数可以表示四维空间中的一个转动。

只有单位四元数才能表示旋转，所以在Eigen中一般会有quaternion.normialzed()进行归一化的处理

任给一个单位四元数q，计算它的虚部，我们就马上可以知道转轴是什么,计算一个单位四元数的实部，它的反余弦值给出旋转角的一半。在四元数表示下，计算转轴和旋转角变得异常简单。

四元数的微分

当我们使用旋转轴加上旋转角表示旋转的时候，我们定义如下

\(v =u \theta\) , u是单位向量，\(\theta = ||v||\)

并且由泰勒展开，我们有，　\(e^v = e^{u\theta} = cos\theta + usin\theta\)

记住一个绕轴ｕ旋转\(\theta\)角度的旋转，表示成四元数的时候是做两次旋转，对应的ｑ是\(cos(\frac {\theta}{2}) + u sin(\frac {\theta}{2})\) = \( \begin{bmatrix} cos(\frac {\theta}{2}) \\ u sin(\frac {\theta}{2}) \\ \end{bmatrix}\)

\[x^{'} = q \bigotimes x \bigotimes q^{*}　= Rx \]

对应的当我们旋转很小的角度，\(\theta\) --> 0的时候，我们对上面的矩阵和ｅ函数求近似值，有

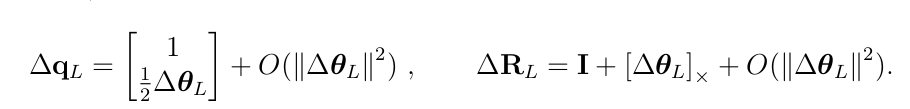
对时间求微分

\[\frac {d q(t)}{dt} = lim \frac{q(t+\Delta t) - q(t)}{\Delta t} \]

代入就有

\[\frac {d R(t)}{dt} = lim \frac{\Delta RR(t) - R(t)}{\Delta t} \]

\[\omega _L = \frac{d\theta _L(t)}{dt} \]

\[\frac{d R^{e}_{b}}{dt} = [\sideset {^e} {}\omega] _{\times} R^{e}_{b} \]

\[\frac{d R^{e}_{b}}{dt} = R^{e}_{b} [\sideset {^b} {}\omega ]_{\times} \]

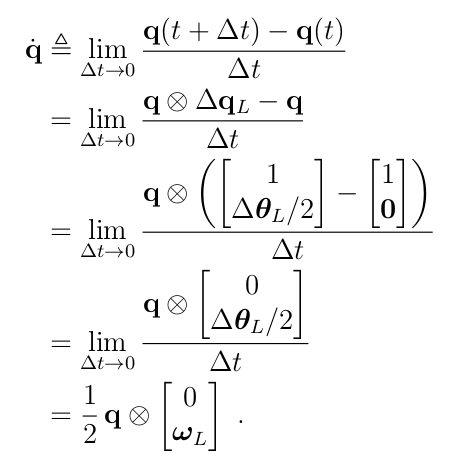
看上面的公式，角速度在不同的坐标系表示下，一个是乘在左边的一个是在右边的，如果把右边的一个Ｒ乘过去，

\[\dot{R(t)}R(t)^T = \phi(t)^\wedge \]

这个是不是很熟悉，就是李群和李代数之间的变换关系。

在下面的那篇论文中可以证明，

说明李群中对应的skew-matrix不是随便选取的(不是只要满足反对成矩阵的性质)，是有一定的方法。\(\omega\)又叫做rotation vector. encodes the angle and axis of rotation

\[\dot q(t) = \frac{1}{2}q(t) \bigotimes \omega(t) \]

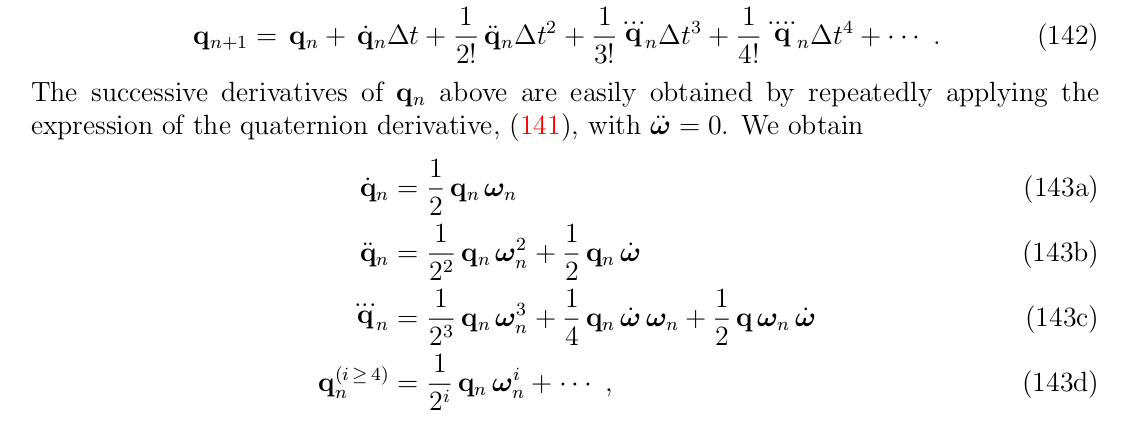
在一段时间内\([t_n,t_{n+1}]\),\(\dot \omega =0\),

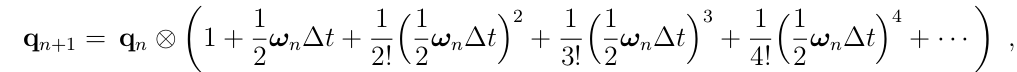
上面的左边就是\(e^{\omega \Delta t/2}\)，根据上面说的这个指数对应的旋转角是\(w_n \Delta t\),所以有，

\[q(n+1) = q(n) \bigotimes q\{w_n \Delta t\} \]

这样我们就有了相邻时刻的四元数关系，上面的所有公式都可以在下面的论文找到。

Quaternion kinematics for the error-state Kalman filter